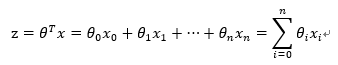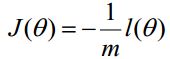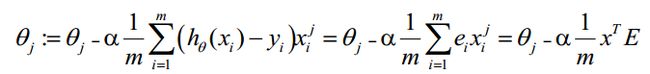matlab 逻辑回归实现,逻辑回归原理介绍及Matlab实现

一、逻辑回归基本概念

1. 什么是逻辑回归

逻辑回归就是这样的一个过程：面对一个回归或者分类问题，建立代价函数，然后通过优化方法迭代求解出最优的模型参数，然后测试验证我们这个求解的模型的好坏。

Logistic回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题(即输出只有两种，分别代表两个类别)

回归模型中，y是一个定性变量，比如y=0或1，logistic方法主要应用于研究某些事件发生的概率

2. 逻辑回归的优缺点

优点：

1)速度快，适合二分类问题

2)简单易于理解，直接看到各个特征的权重

3)能容易地更新模型吸收新的数据

缺点：

对数据和场景的适应能力有局限性，不如决策树算法适应性那么强

3. 逻辑回归和多重线性回归的区别

Logistic回归与多重线性回归实际上有很多相同之处，最大的区别就在于它们的因变量不同，其他的基本都差不多。正是因为如此，这两种回归可以归于同一个家族，即广义线性模型(generalizedlinear model)。

这一家族中的模型形式基本上都差不多，不同的就是因变量不同。这一家族中的模型形式基本上都差不多，不同的就是因变量不同。

如果是连续的，就是多重线性回归

如果是二项分布，就是Logistic回归

如果是Poisson分布，就是Poisson回归

如果是负二项分布，就是负二项回归

4. 逻辑回归用途

寻找危险因素：寻找某一疾病的危险因素等；

预测：根据模型，预测在不同的自变量情况下，发生某病或某种情况的概率有多大；

判别：实际上跟预测有些类似，也是根据模型，判断某人属于某病或属于某种情况的概率有多大，也就是看一下这个人有多大的可能性是属于某病。

5. Regression 常规步骤

寻找h函数(即预测函数)

构造J函数(损失函数)

想办法使得J函数最小并求得回归参数(θ)

6. 构造预测函数h(x)

1) Logistic函数(或称为Sigmoid函数)，函数形式为：

 

对于线性边界的情况，边界形式如下：

其中，训练数据为向量

 

最佳参数

构造预测函数为：

函数h(x)的值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别为：

P(y=1│x;θ)=h_θ (x)

P(y=0│x;θ)=1-h_θ (x)

7.构造损失函数J(m个样本，每个样本具有n个特征)

Cost函数和J函数如下，它们是基于最大似然估计推导得到的。

8. 损失函数详细推导过程

1) 求代价函数

概率综合起来写成：

 

取似然函数为：

 

对数似然函数为：

最大似然估计就是求使l(θ)取最大值时的θ，其实这里可以使用梯度上升法求解，求得的θ就是要求的最佳参数。

在Andrew Ng的课程中将J(θ)取为下式，即：

2) 梯度下降法求解最小值

θ更新过程可以写成：

9. 向量化

ectorization是使用矩阵计算来代替for循环，以简化计算过程，提高效率。

向量化过程：

约定训练数据的矩阵形式如下，x的每一行为一条训练样本，而每一列为不同的特称取值：

 

g(A)的参数A为一列向量，所以实现g函数时要支持列向量作为参数，并返回列向量。

θ更新过程可以改为：

综上所述，Vectorization后θ更新的步骤如下：

求 A=x*θ

求 E=g(A)-y

求

10.正则化

(1) 过拟合问题

过拟合即是过分拟合了训练数据，使得模型的复杂度提高，繁华能力较差(对未知数据的预测能力)

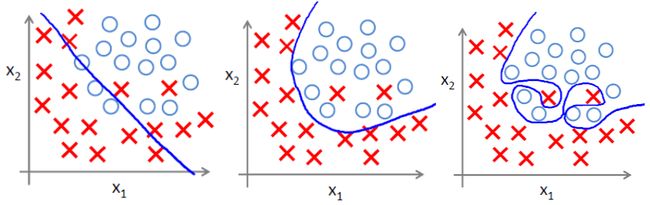
下面左图即为欠拟合，中图为合适的拟合，右图为过拟合。

(2)过拟合主要原因

过拟合问题往往源自过多的特征

解决方法

1)减少特征数量(减少特征会失去一些信息，即使特征选的很好)

• 可用人工选择要保留的特征；

• 模型选择算法；

2)正则化(特征较多时比较有效)

• 保留所有特征，但减少θ的大小

(3)正则化方法

正则化是结构风险最小化策略的实现，是在经验风险上加一个正则化项或惩罚项。正则化项一般是模型复杂度的单调递增函数，模型越复杂，正则化项就越大。

正则项可以取不同的形式，在回归问题中取平方损失，就是参数的L2范数，也可以取L1范数。取平方损失时，模型的损失函数变为：

lambda是正则项系数：

• 如果它的值很大，说明对模型的复杂度惩罚大，对拟合数据的损失惩罚小，这样它就不会过分拟合数据，在训练数据上的偏差较大，在未知数据上的方差较小，但是可能出现欠拟合的现象；

• 如果它的值很小，说明比较注重对训练数据的拟合，在训练数据上的偏差会小，但是可能会导致过拟合。

正则化后的梯度下降算法θ的更新变为：

二、Matlab实现逻辑回归

clear

clc

X = xlsread('C:\Users\user01\Desktop\test.xlsx');

[m,n] = size(X);

%数据归一化处理

X(:,1)=X(:,1)/max(X(:,1));

X(:,2)=X(:,2)/max(X(:,2));

X(:,3)=X(:,3)/max(X(:,3));

X(:,4)=X(:,4)/max(X(:,4));

X(:,5)=X(:,5)/max(X(:,5));

X(:,6)=X(:,6)/max(X(:,6));

%将截距项添加至数据集X

%X=[X,ones(m,1)];

Y=X(:,7);

%我们把数据集中所有序号末位为6的设定为测试集，其他的数据为训练集

%将数据分为训练集XX1,YY1，测试集XX2,YY2。

j=1;

k=1;

for i=1:m

if mod(i,10)==9

XX2(j,:)=X(i,:);

YY2(j,:)=Y(i,:);

j=j+1;

else

XX1(k,:)=X(i,:);

YY1(k,:)=Y(i,:);

k=k+1;

end

end

[m1,n1] = size(XX1);

[m2,n2] = size(XX2);

%设定学习率为0.01

delta=0.01;

%收敛到的极值是否与初值无关还待验证

theta1=rand(6,1);

%训练模型

%向量化求解theta

%迭代次数num

% num = 100;

% while(num)

% xx = XX1(:,1:4)';

% yy = YY1;

% A = xx' * theta1;

% g = 1/(1+exp(-A));

% E = g' - yy;

% theta2 = theta1 - delta * xx * E;

%

% % temp = theta2-theta1;

% % theta = norm(temp);

% theta1 = theta2;

% num = num - 1;

% end

%%训练模型

%公式法求解theta

num = 100;

while(num)

dt=zeros(6,1);

for i=1:m1

xx=XX1(i,1:6)';

yy=YY1(i,1);

h=1/(1+exp(-(theta1' * xx)));

dt=dt+(yy-h) * xx;

end

%theta2=theta1+delta*dt;

theta2=theta1 - 1/m1*delta*dt;

%norm(theta2-theta1)

%0.00001

%norm(A) 返回向量A的2范数

temp = theta2-theta1;

theta = norm(temp);

theta1=theta2;

num = num - 1;

end

%测试数据

cc=0;

for i=1:m2

xx=XX2(i,1:6)';

yy=YY2(i);

ans=1/(1+exp(-theta2' * xx));

if ans>0.5 && yy==1

cc=cc+1;

end

if ans<=0.5 && yy==0

cc=cc+1;

end

end

cc/m2

%测试结果： 正确率为 75.73%。