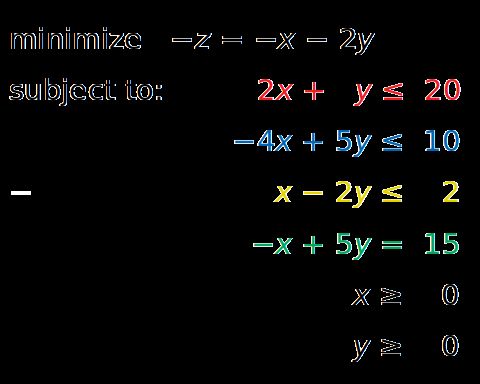只需一步，轻松用Python实现线性规划

线性规划说明

什么是线性规划？

想象一下，您有一个线性方程组和不等式系统。这样的系统通常有许多可能的解决方案。线性规划是一组数学和计算工具，可让您找到该系统的特定解，该解对应于某些其他线性函数的最大值或最小值。

什么是混合整数线性规划？

混合整数线性规划是线性规划的扩展。它处理至少一个变量采用离散整数而不是连续值的问题。尽管乍一看混合整数问题与连续变量问题相似，但它们在灵活性和精度方面具有显着优势。

整数变量对于正确表示自然用整数表示的数量很重要，例如生产的飞机数量或服务的客户数量。

一种特别重要的整数变量是二进制变量。它只能取零或一的值，在做出是或否的决定时很有用，例如是否应该建造工厂或者是否应该打开或关闭机器。您还可以使用它们来模拟逻辑约束。

为什么线性规划很重要？

线性规划是一种基本的优化技术，已在科学和数学密集型领域使用了数十年。它精确、相对快速，适用于一系列实际应用。

混合整数线性规划允许您克服线性规划的许多限制。您可以使用分段线性函数近似非线性函数、使用半连续变量、模型逻辑约束等。它是一种计算密集型工具，但计算机硬件和软件的进步使其每天都更加适用。

通常，当人们试图制定和解决优化问题时，第一个问题是他们是否可以应用线性规划或混合整数线性规划。

以下文章说明了线性规划和混合整数线性规划的一些用例：

• Gurobi 优化案例研究
• 线性规划技术的五个应用领域

随着计算机能力的增强、算法的改进以及更多用户友好的软件解决方案的出现，线性规划，尤其是混合整数线性规划的重要性随着时间的推移而增加。

使用 Python 进行线性规划

解决线性规划问题的基本方法称为单纯形法，它有多种变体。另一种流行的方法是内点法。

混合整数线性规划问题可以通过更复杂且计算量更大的方法来解决，例如分支定界法，它在幕后使用线性规划。这种方法的一些变体是分支和切割方法，它涉及使用切割平面，以及分支和价格方法。

有几种适用于线性规划和混合整数线性规划的合适且众所周知的 Python 工具。其中一些是开源的，而另一些是专有的。您是否需要免费或付费工具取决于问题的规模和复杂性，以及对速度和灵活性的需求。

值得一提的是，几乎所有广泛使用的线性规划和混合整数线性规划库都是以 Fortran 或 C 或 C++ 原生和编写的。这是因为线性规划需要对（通常很大）矩阵进行计算密集型工作。此类库称为求解器。Python 工具只是求解器的包装器。

Python 适合围绕本机库构建包装器，因为它可以很好地与 C/C++ 配合使用。对于本教程，您不需要任何 C/C++（或 Fortran），但如果您想了解有关此酷功能的更多信息，请查看以下资源：

• 构建 Python C 扩展模块
• CPython 内部
• 用 C 或 C++ 扩展 Python

基本上，当您定义和求解模型时，您使用 Python 函数或方法调用低级库，该库执行实际优化工作并将解决方案返回给您的 Python 对象。

几个免费的 Python 库专门用于与线性或混合整数线性规划求解器交互：

• SciPy Optimization and Root Finding
• PuLP
• Pyomo
• CVXOPT

在本教程中，您将使用SciPy和PuLP来定义和解决线性规划问题。

线性规划示例

在本节中，您将看到线性规划问题的两个示例：

1. 一个说明什么是线性规划的小问题
2. 一个与资源分配相关的实际问题，它说明了现实世界场景中的线性规划概念

您将在下一节中使用 Python 来解决这两个问题。

小型线性规划问题

考虑以下线性规划问题：

你需要找到X和Ÿ使得红色，蓝色和黄色的不平等，以及不平等X ≥0和ÿ ≥0，是满意的。同时，您的解决方案必须对应于z的最大可能值。

您需要找到的自变量（在本例中为x和y）称为决策变量。要最大化或最小化的决策变量的函数（在本例中为z）称为目标函数、成本函数或仅称为目标。您需要满足的不等式称为不等式约束。您还可以在称为等式约束的约束中使用方程。

这是您如何可视化问题的方法：

红线代表的功能2 X + Ý = 20，和它上面的红色区域示出了红色不等式不满足。同样，蓝线是函数−4 x + 5 y = 10，蓝色区域被禁止，因为它违反了蓝色不等式。黄线是 − x + 2 y = −2，其下方的黄色区域是黄色不等式无效的地方。

如果您忽略红色、蓝色和黄色区域，则仅保留灰色区域。灰色区域的每个点都满足所有约束，是问题的潜在解决方案。该区域称为可行域，其点为可行解。在这种情况下，有无数可行的解决方案。

您想最大化z。对应于最大z的可行解是最优解。如果您尝试最小化目标函数，那么最佳解决方案将对应于其可行的最小值。

请注意，z是线性的。你可以把它想象成一个三维空间中的平面。这就是为什么最优解必须在可行区域的顶点或角上的原因。在这种情况下，最佳解决方案是红线和蓝线相交的点，稍后您将看到。

有时，可行区域的整个边缘，甚至整个区域，都可以对应相同的z值。在这种情况下，您有许多最佳解决方案。

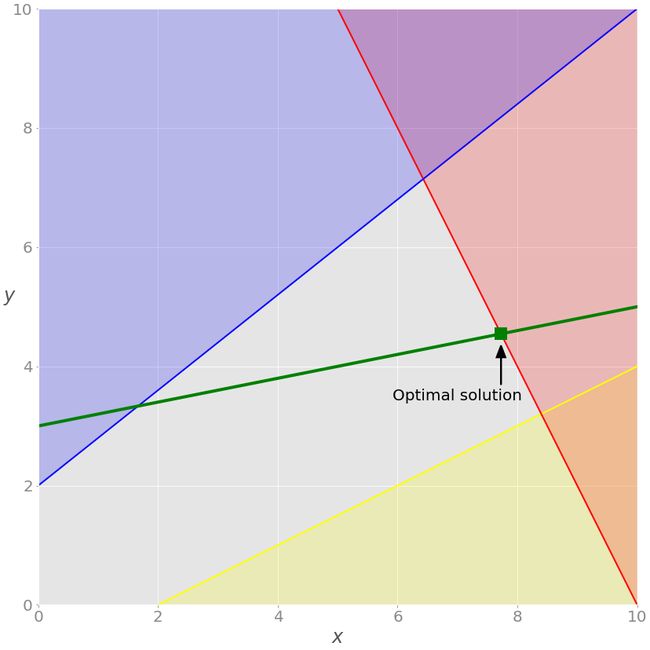
您现在已准备好使用绿色显示的附加等式约束来扩展问题：

方程式 − x + 5 y = 15，以绿色书写，是新的。这是一个等式约束。您可以通过向上一张图像添加相应的绿线来将其可视化：

现在的解决方案必须满足绿色等式，因此可行区域不再是整个灰色区域。它是绿线从与蓝线的交点到与红线的交点穿过灰色区域的部分。后一点是解决方案。

如果插入x的所有值都必须是整数的要求，那么就会得到一个混合整数线性规划问题，可行解的集合又会发生变化：

您不再有绿线，只有沿线的x值为整数的点。可行解是灰色背景上的绿点，此时最优解离红线最近。

这三个例子说明了可行的线性规划问题，因为它们具有有界可行区域和有限解。

不可行的线性规划问题

如果没有解，线性规划问题是不可行的。当没有解决方案可以同时满足所有约束时，通常会发生这种情况。

例如，考虑如果添加约束x + y ≤ −1会发生什么。那么至少有一个决策变量（x或y）必须是负数。这与给定的约束x ≥ 0 和y ≥ 0相冲突。这样的系统没有可行的解决方案，因此称为不可行的。

另一个示例是添加与绿线平行的第二个等式约束。这两行没有共同点，因此不会有满足这两个约束的解决方案。

无界线性规划问题

一个线性规划问题是无界的，如果它的可行区域是无界，将溶液不是有限。这意味着您的变量中至少有一个不受约束，可以达到正无穷大或负无穷大，从而使目标也无限大。

例如，假设您采用上面的初始问题并删除红色和黄色约束。从问题中删除约束称为放松问题。在这种情况下，x和y不会在正侧有界。您可以将它们增加到正无穷大，从而产生无限大的z值。

资源分配问题

在前面的部分中，您研究了一个与任何实际应用程序无关的抽象线性规划问题。在本小节中，您将找到与制造业资源分配相关的更具体和实用的优化问题。

假设一家工厂生产四种不同的产品，第一种产品的日产量为x ₁，第二种产品的产量为x 2，依此类推。目标是确定每种产品的利润最大化日产量，同时牢记以下条件：

1. 第一种、第二种、第三种和第四种产品的每单位产品利润分别为 20 美元、12 美元、40 美元和 25 美元。
2. 由于人力限制，每天生产的总数量不能超过五十台。
3. 对于每单位第一个产品，消耗三个单位的原材料 A。每单位第二产品需要两单位原料 A 和一单位原料 B。每单位第三产品需要一单位 A 和两单位 B。最后，每单位第四产品需要三B 的单位
4. 由于运输和储存的限制，工厂每天最多可以消耗一百单位的原材料 A 和九十单位的 B。

数学模型可以这样定义：

目标函数（利润）在条件 1 中定义。人力约束遵循条件 2。对原材料 A 和 B 的约束可以从条件 3 和条件 4 中通过对每种产品的原材料需求求和得出。

最后，产品数量不能为负，因此所有决策变量必须大于或等于零。

与前面的示例不同，您无法方便地将其可视化，因为它有四个决策变量。但是，无论问题的维度如何，原理都是相同的。

线性规划 Python 实现

在本教程中，您将使用两个Python 包来解决上述线性规划问题：

1. SciPy是一个用于使用 Python 进行科学计算的通用包。
2. PuLP是一个 Python 线性编程 API，用于定义问题和调用外部求解器。

SciPy 设置起来很简单。安装后，您将拥有开始所需的一切。它的子包scipy.optimize可用于线性和非线性优化。

PuLP 允许您选择求解器并以更自然的方式表述问题。PuLP 使用的默认求解器是COIN-OR Branch and Cut Solver (CBC)。它连接到用于线性松弛的COIN-OR 线性规划求解器 (CLP)和用于切割生成的COIN-OR 切割生成器库 (CGL)。

另一个伟大的开源求解器是GNU 线性规划工具包 (GLPK)。一些著名且非常强大的商业和专有解决方案是Gurobi、CPLEX和XPRESS。

除了在定义问题时提供灵活性和运行各种求解器的能力外，PuLP 使用起来不如 Pyomo 或 CVXOPT 等替代方案复杂，后者需要更多的时间和精力来掌握。

安装 SciPy 和 PuLP

要学习本教程，您需要安装 SciPy 和 PuLP。下面的示例使用 SciPy 1.4.1 版和 PuLP 2.1 版。

您可以使用pip以下方法安装两者：

$ python -m pip install -U "scipy==1.4.*" "pulp==2.1"

您可能需要运行pulptest或sudo pulptest启用 PuLP 的默认求解器，尤其是在您使用 Linux 或 Mac 时：

$ pulptest

或者，您可以下载、安装和使用 GLPK。它是免费和开源的，适用于 Windows、MacOS 和 Linux。在本教程的后面部分，您将看到如何将 GLPK（除了 CBC）与 PuLP 一起使用。

在 Windows 上，您可以下载档案并运行安装文件。

在 MacOS 上，您可以使用 Homebrew：

$ brew install glpk

在 Debian 和 Ubuntu 上，使用apt来安装glpk和glpk-utils：

$ sudo apt install glpk glpk-utils

在Fedora，使用dnf具有glpk-utils：

$ sudo dnf install glpk-utils

您可能还会发现conda对安装 GLPK 很有用：

$ conda install -c conda-forge glpk

安装完成后，可以查看GLPK的版本：

$ glpsol --version

有关详细信息，请参阅 GLPK 关于使用Windows 可执行文件和Linux 软件包进行安装的教程。

使用 SciPy

在本节中，您将学习如何使用 SciPy优化和求根库进行线性规划。

要使用 SciPy 定义和解决优化问题，您需要导入scipy.optimize.linprog()：

>>>
>>> from scipy.optimize import linprog

现在您已经linprog()导入，您可以开始优化。

示例 1

让我们首先解决上面的线性规划问题：

linprog()仅解决最小化（而非最大化）问题，并且不允许具有大于或等于符号 (≥) 的不等式约束。要解决这些问题，您需要在开始优化之前修改您的问题：

• 不是最大化z = x + 2 y，你可以最小化它的负值（− z = − x − 2 y）。
• 代替大于或等于符号，您可以将黄色不等式乘以 -1 并得到小于或等于符号 (≤) 的相反数。

引入这些更改后，您将获得一个新系统：

该系统与原始系统等效，并且将具有相同的解决方案。应用这些更改的唯一原因是克服 SciPy 与问题表述相关的局限性。

下一步是定义输入值：

>>>
>>> obj = [-1, -2]
>>> #      ─┬  ─┬
>>> #       │   └┤ Coefficient for y
>>> #       └────┤ Coefficient for x

>>> lhs_ineq = [[ 2,  1],  # Red constraint left side
...             [-4,  5],  # Blue constraint left side
...             [ 1, -2]]  # Yellow constraint left side

>>> rhs_ineq = [20,  # Red constraint right side
...             10,  # Blue constraint right side
...              2]  # Yellow constraint right side

>>> lhs_eq = [[-1, 5]]  # Green constraint left side
>>> rhs_eq = [15]       # Green constraint right side

您将上述系统中的值放入适当的列表、元组或NumPy 数组中：

• obj 保存目标函数的系数。
• lhs_ineq 保存不等式（红色、蓝色和黄色）约束的左侧系数。
• rhs_ineq 保存不等式（红色、蓝色和黄色）约束的右侧系数。
• lhs_eq 保存来自等式（绿色）约束的左侧系数。
• rhs_eq 保存来自等式（绿色）约束的右侧系数。

注意：请注意行和列的顺序！

约束左侧和右侧的行顺序必须相同。每一行代表一个约束。

来自目标函数和约束左侧的系数的顺序必须匹配。每列对应一个决策变量。

下一步是以与系数相同的顺序定义每个变量的界限。在这种情况下，它们都在零和正无穷大之间：

>>>
>>> bnd = [(0, float("inf")),  # Bounds of x
...        (0, float("inf"))]  # Bounds of y

此语句是多余的，因为linprog()默认情况下采用这些边界（零到正无穷大）。

注：相反的float("inf")，你可以使用math.inf，numpy.inf或scipy.inf。

最后，是时候优化和解决您感兴趣的问题了。你可以这样做linprog()：

>>>
>>> opt = linprog(c=obj, A_ub=lhs_ineq, b_ub=rhs_ineq,
...               A_eq=lhs_eq, b_eq=rhs_eq, bounds=bnd,
...               method="revised simplex")
>>> opt
     con: array([0.])
     fun: -16.818181818181817
 message: 'Optimization terminated successfully.'
     nit: 3
   slack: array([ 0.        , 18.18181818,  3.36363636])
  status: 0
 success: True
       x: array([7.72727273, 4.54545455])

参数c是指来自目标函数的系数。A_ub和b_ub分别与不等式约束左边和右边的系数有关。同样，A_eq并b_eq参考等式约束。您可以使用bounds提供决策变量的下限和上限。

您可以使用该参数method来定义要使用的线性规划方法。有以下三种选择：

1. method="interior-point"选择内点法。默认情况下设置此选项。
2. method="revised simplex" 选择修正的两相单纯形法。
3. method="simplex" 选择传统的两相单纯形方法。

linprog() 返回具有以下属性的数据结构：

• .con 是等式约束残差。
• .fun 是最优的目标函数值（如果找到）。
• .message 是解决方案的状态。
• .nit 是完成计算所需的迭代次数。
• .slack 是松弛变量的值，或约束左右两侧的值之间的差异。
• .status是一个介于0和之间的整数4，表示解决方案的状态，例如0找到最佳解决方案的时间。
• .success是一个布尔值，显示是否已找到最佳解决方案。
• .x 是一个保存决策变量最优值的 NumPy 数组。

您可以分别访问这些值：

>>>
>>> opt.fun
-16.818181818181817

>>> opt.success
True

>>> opt.x
array([7.72727273, 4.54545455])

这就是您获得优化结果的方式。您还可以以图形方式显示它们：

如前所述，线性规划问题的最优解位于可行区域的顶点。在这种情况下，可行区域只是蓝线和红线之间的绿线部分。最优解是代表绿线和红线交点的绿色方块。

如果要排除相等（绿色）约束，只需删除参数A_eq并b_eq从linprog()调用中删除：

>>>
>>> opt = linprog(c=obj, A_ub=lhs_ineq, b_ub=rhs_ineq, bounds=bnd,
...               method="revised simplex")
>>> opt
     con: array([], dtype=float64)
     fun: -20.714285714285715
 message: 'Optimization terminated successfully.'
     nit: 2
   slack: array([0.        , 0.        , 9.85714286])
  status: 0
 success: True
       x: array([6.42857143, 7.14285714]))

解决方案与前一种情况不同。你可以在图表上看到：

在这个例子中，最优解是红色和蓝色约束相交的可行（灰色）区域的紫色顶点。其他顶点，如黄色顶点，具有更高的目标函数值。

示例 2

您可以使用 SciPy 来解决前面部分所述的资源分配问题：

和前面的例子一样，你需要从上面的问题中提取必要的向量和矩阵，将它们作为参数传递给.linprog()，然后得到结果：

>>>
>>> obj = [-20, -12, -40, -25]

>>> lhs_ineq = [[1, 1, 1, 1],  # Manpower
...             [3, 2, 1, 0],  # Material A
...             [0, 1, 2, 3]]  # Material B

>>> rhs_ineq = [ 50,  # Manpower
...             100,  # Material A
...              90]  # Material B

>>> opt = linprog(c=obj, A_ub=lhs_ineq, b_ub=rhs_ineq,
...               method="revised simplex")
>>> opt
     con: array([], dtype=float64)
     fun: -1900.0
 message: 'Optimization terminated successfully.'
     nit: 2
   slack: array([ 0., 40.,  0.])
  status: 0
 success: True
       x: array([ 5.,  0., 45.,  0.])

结果告诉您最大利润是1900并且对应于x ₁ = 5 和x ₃ = 45。在给定条件下生产第二和第四个产品是没有利润的。您可以在这里得出几个有趣的结论：

1. 第三个产品带来的单位利润最大，因此工厂将生产最多。
2. 第一个slack是0，表示人力（第一）约束左右两边的值是一样的。工厂每天50生产单位，这是它的全部产能。
3. 第二个松弛是40因为工厂消耗了 60 单位的原材料 A（第一种产品为 15 单位，第三种产品为 45100单位）。
4. 第三个裕量是0，这意味着工厂消耗了所有90单位的原材料 B。这全部量都用于第三个产品。这就是为什么工厂根本不能生产第二或第四种产品，也不能生产超过45单位的第三种产品。缺乏原材料 B.

opt.statusis0和opt.successis True，说明优化问题成功求解，最优可行解。

SciPy 的线性规划功能主要用于较小的问题。对于更大和更复杂的问题，您可能会发现其他库更适合，原因如下：

• SciPy 无法运行各种外部求解器。
• SciPy 不能使用整数决策变量。
• SciPy 不提供促进模型构建的类或函数。您必须定义数组和矩阵，这对于大型问题来说可能是一项乏味且容易出错的任务。
• SciPy 不允许您直接定义最大化问题。您必须将它们转换为最小化问题。
• SciPy 不允许您直接使用大于或等于符号来定义约束。您必须改用小于或等于。

幸运的是，Python 生态系统为线性编程提供了几种替代解决方案，这些解决方案对于更大的问题非常有用。其中之一是 PuLP，您将在下一节中看到它的实际应用。

Using PuLP

PuLP 具有比 SciPy 更方便的线性编程 API。您不必在数学上修改您的问题或使用向量和矩阵。一切都更干净，更不容易出错。

像往常一样，您首先导入您需要的内容：

from pulp import LpMaximize, LpProblem, LpStatus, lpSum, LpVariable

现在您已经导入了 PuLP，您可以解决您的问题。

示例 1

您现在将使用 PuLP 解决此系统：

第一步是初始化一个实例LpProblem来表示你的模型：

# Create the model
model = LpProblem(name="small-problem", sense=LpMaximize)

您可以使用该sense参数来选择是执行最小化（LpMinimize或1，这是默认值）还是最大化（LpMaximize或-1）。这个选择会影响你的问题的结果。

一旦有了模型，就可以将决策变量定义为LpVariable类的实例：

# Initialize the decision variables
x = LpVariable(name="x", lowBound=0)
y = LpVariable(name="y", lowBound=0)

您需要提供下限，lowBound=0因为默认值为负无穷大。该参数upBound定义了上限，但您可以在此处省略它，因为它默认为正无穷大。

可选参数cat定义决策变量的类别。如果您使用的是连续变量，则可以使用默认值"Continuous"。

您可以使用变量x和y创建表示线性表达式和约束的其他 PuLP 对象：

>>>
>>> expression = 2 * x + 4 * y
>>> type(expression)


>>> constraint = 2 * x + 4 * y >= 8
>>> type(constraint)

当您将决策变量与标量相乘或构建多个决策变量的线性组合时，您会得到一个pulp.LpAffineExpression代表线性表达式的实例。

注意：您可以增加或减少变量或表达式，你可以乘他们常数，因为纸浆类实现一些Python的特殊方法，即模拟数字类型一样__add__()，__sub__()和__mul__()。这些方法用于像定制运营商的行为+，-和*。

类似地，您可以将线性表达式、变量和标量与运算符 ==、<=、 或>=以获取表示模型线性约束的纸浆.LpConstraint实例。

注：也有可能与丰富的比较方法来构建的约束.__eq__()，.__le__()以及.__ge__()定义了运营商的行为==，<=和>=。

考虑到这一点，下一步是创建约束和目标函数并将它们分配给您的模型。您不需要创建列表或矩阵。只需编写 Python 表达式并使用+=运算符将它们附加到模型中：

# Add the constraints to the model
model += (2 * x + y <= 20, "red_constraint")
model += (4 * x - 5 * y >= -10, "blue_constraint")
model += (-x + 2 * y >= -2, "yellow_constraint")
model += (-x + 5 * y == 15, "green_constraint")

在上面的代码中，您定义了包含约束及其名称的元组。LpProblem允许您通过将约束指定为元组来向模型添加约束。第一个元素是一个LpConstraint实例。第二个元素是该约束的可读名称。

设置目标函数非常相似：

# Add the objective function to the model
obj_func = x + 2 * y
model += obj_func

或者，您可以使用更短的符号：

# Add the objective function to the model
model += x + 2 * y

现在您已经添加了目标函数并定义了模型。

注意：您可以使用运算符将​​约束或目标附加到模型中，+=因为它的类LpProblem实现了特殊方法.__iadd__()，该方法用于指定 的行为+=。

对于较大的问题，lpSum()与列表或其他序列一起使用通常比重复+运算符更方便。例如，您可以使用以下语句将目标函数添加到模型中：

# Add the objective function to the model
model += lpSum([x, 2 * y])

它产生与前一条语句相同的结果。

您现在可以看到此模型的完整定义：

>>>
>>> model
small-problem:
MAXIMIZE
1*x + 2*y + 0
SUBJECT TO
red_constraint: 2 x + y <= 20

blue_constraint: 4 x - 5 y >= -10

yellow_constraint: - x + 2 y >= -2

green_constraint: - x + 5 y = 15

VARIABLES
x Continuous
y Continuous

模型的字符串表示包含所有相关数据：变量、约束、目标及其名称。

注意：字符串表示是通过定义特殊方法构建的.__repr__()。有关 的更多详细信息.__repr__()，请查看Pythonic OOP 字符串转换：__repr__vs__str__ .

最后，您已准备好解决问题。你可以通过调用.solve()你的模型对象来做到这一点。如果要使用默认求解器 (CBC)，则不需要传递任何参数：

# Solve the problem
status = model.solve()

.solve()调用底层求解器，修改model对象，并返回解决方案的整数状态，1如果找到了最优解。有关其余状态代码，请参阅LpStatus[]。

你可以得到优化结果作为 的属性model。该函数value()和相应的方法.value()返回属性的实际值：

>>>
>>> print(f"status: {model.status}, {LpStatus[model.status]}")
status: 1, Optimal

>>> print(f"objective: {model.objective.value()}")
objective: 16.8181817

>>> for var in model.variables():
...     print(f"{var.name}: {var.value()}")
...
x: 7.7272727
y: 4.5454545

>>> for name, constraint in model.constraints.items():
...     print(f"{name}: {constraint.value()}")
...
red_constraint: -9.99999993922529e-08
blue_constraint: 18.181818300000003
yellow_constraint: 3.3636362999999996
green_constraint: -2.0000000233721948e-07)

model.objective持有目标函数model.constraints的值，包含松弛变量的值，以及对象x和y具有决策变量的最优值。model.variables()返回一个包含决策变量的列表：

>>>
>>> model.variables()
[x, y]
>>> model.variables()[0] is x
True
>>> model.variables()[1] is y
True

如您所见，此列表包含使用 的构造函数创建的确切对象LpVariable。

结果与您使用 SciPy 获得的结果大致相同。

注意：注意这个方法.solve()——它会改变对象的状态，x并且y！

您可以通过调用查看使用了哪个求解器.solver：

>>>
>>> model.solver

输出通知您求解器是 CBC。您没有指定求解器，因此 PuLP 调用了默认求解器。

如果要运行不同的求解器，则可以将其指定为 的参数.solve()。例如，如果您想使用 GLPK 并且已经安装了它，那么您可以solver=GLPK(msg=False)在最后一行使用。请记住，您还需要导入它：

from pulp import GLPK

现在你已经导入了 GLPK，你可以在里面使用它.solve()：

# Create the model
model = LpProblem(name="small-problem", sense=LpMaximize)

# Initialize the decision variables
x = LpVariable(name="x", lowBound=0)
y = LpVariable(name="y", lowBound=0)

# Add the constraints to the model
model += (2 * x + y <= 20, "red_constraint")
model += (4 * x - 5 * y >= -10, "blue_constraint")
model += (-x + 2 * y >= -2, "yellow_constraint")
model += (-x + 5 * y == 15, "green_constraint")

# Add the objective function to the model
model += lpSum([x, 2 * y])

# Solve the problem
status = model.solve(solver=GLPK(msg=False))

该msg参数用于显示来自求解器的信息。msg=False禁用显示此信息。如果要包含信息，则只需省略msg或设置msg=True。

您的模型已定义并求解，因此您可以按照与前一种情况相同的方式检查结果：

>>>
>>> print(f"status: {model.status}, {LpStatus[model.status]}")
status: 1, Optimal

>>> print(f"objective: {model.objective.value()}")
objective: 16.81817

>>> for var in model.variables():
...     print(f"{var.name}: {var.value()}")
...
x: 7.72727
y: 4.54545

>>> for name, constraint in model.constraints.items():
...     print(f"{name}: {constraint.value()}")
...
red_constraint: -1.0000000000509601e-05
blue_constraint: 18.181830000000005
yellow_constraint: 3.3636299999999997
green_constraint: -2.000000000279556e-05

使用 GLPK 得到的结果与使用 SciPy 和 CBC 得到的结果几乎相同。

一起来看看这次用的是哪个求解器：

>>>
>>> model.solver

正如您在上面用突出显示的语句定义的那样model.solve(solver=GLPK(msg=False))，求解器是 GLPK。

您还可以使用 PuLP 来解决混合整数线性规划问题。要定义整数或二进制变量，只需传递cat="Integer"或cat="Binary"到LpVariable。其他一切都保持不变：

# Create the model
model = LpProblem(name="small-problem", sense=LpMaximize)

# Initialize the decision variables: x is integer, y is continuous
x = LpVariable(name="x", lowBound=0, cat="Integer")
y = LpVariable(name="y", lowBound=0)

# Add the constraints to the model
model += (2 * x + y <= 20, "red_constraint")
model += (4 * x - 5 * y >= -10, "blue_constraint")
model += (-x + 2 * y >= -2, "yellow_constraint")
model += (-x + 5 * y == 15, "green_constraint")

# Add the objective function to the model
model += lpSum([x, 2 * y])

# Solve the problem
status = model.solve()

在本例中，您有一个整数变量并获得与之前不同的结果：

>>>
>>> print(f"status: {model.status}, {LpStatus[model.status]}")
status: 1, Optimal

>>> print(f"objective: {model.objective.value()}")
objective: 15.8

>>> for var in model.variables():
...     print(f"{var.name}: {var.value()}")
...
x: 7.0
y: 4.4

>>> for name, constraint in model.constraints.items():
...     print(f"{name}: {constraint.value()}")
...
red_constraint: -1.5999999999999996
blue_constraint: 16.0
yellow_constraint: 3.8000000000000007
green_constraint: 0.0)

>>> model.solver

Nowx是一个整数，如模型中所指定。（从技术上讲，它保存一个小数点后为零的浮点值。）这一事实改变了整个解决方案。让我们在图表上展示这一点：

如您所见，最佳解决方案是灰色背景上最右边的绿点。这是两者的最大价值的可行的解决方案x和y，给它的最大目标函数值。

GLPK 也能够解决此类问题。

示例 2

现在你可以使用 PuLP 来解决上面的资源分配问题：

定义和解决问题的方法与前面的示例相同：

# Define the model
model = LpProblem(name="resource-allocation", sense=LpMaximize)

# Define the decision variables
x = {i: LpVariable(name=f"x{i}", lowBound=0) for i in range(1, 5)}

# Add constraints
model += (lpSum(x.values()) <= 50, "manpower")
model += (3 * x[1] + 2 * x[2] + x[3] <= 100, "material_a")
model += (x[2] + 2 * x[3] + 3 * x[4] <= 90, "material_b")

# Set the objective
model += 20 * x[1] + 12 * x[2] + 40 * x[3] + 25 * x[4]

# Solve the optimization problem
status = model.solve()

# Get the results
print(f"status: {model.status}, {LpStatus[model.status]}")
print(f"objective: {model.objective.value()}")

for var in x.values():
    print(f"{var.name}: {var.value()}")

for name, constraint in model.constraints.items():
    print(f"{name}: {constraint.value()}")

在这种情况下，您使用字典 x来存储所有决策变量。这种方法很方便，因为字典可以将决策变量的名称或索引存储为键，将相应的LpVariable对象存储为值。列表或元组的LpVariable实例可以是有用的。

上面的代码产生以下结果：

status: 1, Optimal
objective: 1900.0
x1: 5.0
x2: 0.0
x3: 45.0
x4: 0.0
manpower: 0.0
material_a: -40.0
material_b: 0.0

如您所见，该解决方案与使用 SciPy 获得的解决方案一致。最有利可图的解决方案是每天生产5.0第一件产品和45.0第三件产品。

让我们把这个问题变得更复杂和有趣。假设由于机器问题，工厂无法同时生产第一种和第三种产品。在这种情况下，最有利可图的解决方案是什么？

现在您有另一个逻辑约束：如果x ₁ 为正数，则x ₃ 必须为零，反之亦然。这是二元决策变量非常有用的地方。您将使用两个二元决策变量y ₁ 和y ₃，它们将表示是否生成了第一个或第三个产品：

 1model = LpProblem(name="resource-allocation", sense=LpMaximize)
 2
 3# Define the decision variables
 4x = {i: LpVariable(name=f"x{i}", lowBound=0) for i in range(1, 5)}
 5y = {i: LpVariable(name=f"y{i}", cat="Binary") for i in (1, 3)}
 6
 7# Add constraints
 8model += (lpSum(x.values()) <= 50, "manpower")
 9model += (3 * x[1] + 2 * x[2] + x[3] <= 100, "material_a")
10model += (x[2] + 2 * x[3] + 3 * x[4] <= 90, "material_b")
11
12M = 100
13model += (x[1] <= y[1] * M, "x1_constraint")
14model += (x[3] <= y[3] * M, "x3_constraint")
15model += (y[1] + y[3] <= 1, "y_constraint")
16
17# Set objective
18model += 20 * x[1] + 12 * x[2] + 40 * x[3] + 25 * x[4]
19
20# Solve the optimization problem
21status = model.solve()
22
23print(f"status: {model.status}, {LpStatus[model.status]}")
24print(f"objective: {model.objective.value()}")
25
26for var in model.variables():
27    print(f"{var.name}: {var.value()}")
28
29for name, constraint in model.constraints.items():
30    print(f"{name}: {constraint.value()}")

除了突出显示的行之外，代码与前面的示例非常相似。以下是差异：

• 第 5 行定义了二元决策变量y[1]并y[3]保存在字典中y。
• 第 12 行定义了一个任意大的数M。100在这种情况下，该值足够大，因为您100每天的数量不能超过单位。
• 第 13 行说如果y[1]为零，则x[1]必须为零，否则它可以是任何非负数。
• 第 14 行说如果y[3]为零，则x[3]必须为零，否则它可以是任何非负数。
• 第 15 行说要么y[1]ory[3]为零（或两者都是），所以要么x[1]or 也x[3]必须为零。

这是解决方案：

status: 1, Optimal
objective: 1800.0
x1: 0.0
x2: 0.0
x3: 45.0
x4: 0.0
y1: 0.0
y3: 1.0
manpower: -5.0
material_a: -55.0
material_b: 0.0
x1_constraint: 0.0
x3_constraint: -55.0
y_constraint: 0.0

事实证明，最佳方法是排除第一种产品而只生产第三种产品。

线性规划求解器

就像有许多资源可以帮助您学习线性规划和混合整数线性规划一样，还有许多具有 Python 包装器的求解器可用。这是部分列表：

• GLPK
• LP Solve
• CLP
• CBC
• CVXOPT
• SciPy
• SCIP with PySCIPOpt
• Gurobi Optimizer
• CPLEX
• XPRESS
• MOSEK

其中一些库，如 Gurobi，包括他们自己的 Python 包装器。其他人使用外部包装器。例如，您看到可以使用 PuLP 访问 CBC 和 GLPK。

结论

您现在知道什么是线性规划以及如何使用 Python 解决线性规划问题。您还了解到 Python 线性编程库只是本机求解器的包装器。当求解器完成其工作时，包装器返回解决方案状态、决策变量值、松弛变量、目标函数等。

原文链接：实践线性规划：使用 Python 进行优化-云社区-华为云
作者：Yuchuan。