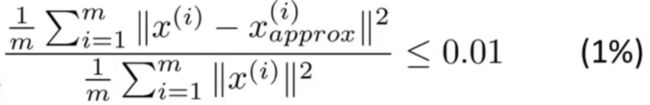十五、非监督学习
\qquad 监督学习和非监督学习的本质区别在于,数据集是否是带有“标签”的,当数据集是有标签的,则属于监督学习的范畴;当数据集没有标签,则属于非监督学习的范畴,如聚类算法就属于非监督学习的范畴。
1、k-means聚类
\qquad k-means聚类算法输入数据是一系列点,之后需要确定出聚类中心的个数,之后计算每一个数据点到每一个中心的距离,将所有数据点分配到里数据点最近的某个数据中心(Cluster Assignment);之后将数据中心进行移动(Cluster Moving),将每一个数据中心移动到分配给它的数据点的中心位置(所有维度的均值位置);之后重新进行数据点的分配。重复上述过程,直到分配给每一个数据中心的数据点不再发生变化,则算法达到收敛,输出聚类结果。
\qquad k-means聚类算法的流程如下图所示:

1.1 k-means聚类的优化目标
\qquad 首先定义 c ( i ) c^{(i)} c(i)表示将数据点 x ( i ) x^{(i)} x(i)分配到哪一个数据中心(1,2,…,K); μ k \mu_k μk表示第k个聚类中心;则 μ c ( i ) \mu_{c^{(i)}} μc(i)表示数据点 x ( i ) x^{(i)} x(i)对应的数据中心。k-means聚类的目标函数如下所示:
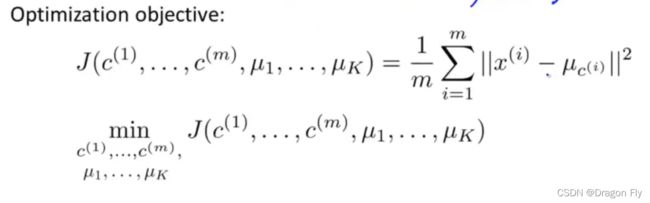

1.2 随机初始化
\qquad 在进行k-means聚类之前,首先选定 K < m K
\qquad 为了避免k-means陷入局部最优,通常采用运行多次k-means算法,记录多次运行k-means算法中成本函数最小的结果作为最优解;通过随机初始化聚类中心的方式来使得k-means算法达到较好的效果。

1.3 选择聚类中心的个数
\qquad 一种方法是使用"拐点"法则(Elbow method),如下图所示:
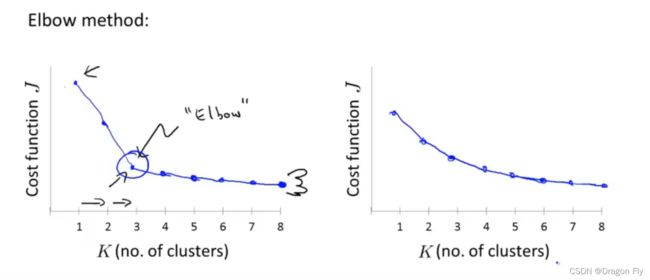
\qquad 如上图左图所示,当有较为清晰的该点出现时,可以使用这种方法;但通常情况下,随着聚类中心数量的增多,成本函数会呈现平滑下降的趋势,如上图右图所示,这样就很难选择出合适的聚类中心个数。
\qquad 很多时候,k-means聚类通常会产生后续的,下游的影响,所以通过聚类结果对于下游的影响也可以作为选择k-means聚类中心个数的重要依据。如服装设计行业,将服装的市场细分为3个或者5个(聚类中心个数),划分越细致,服装的尺寸越适合顾客,但是相应的价格会越高,所以可以通过k-means权衡出将服装尺寸细分称为多少个聚类中心最为合适。
2、维度缩减-Dimension Reduction
\qquad 为了减少特征的数量,可以采用维度缩减的方法来将多维的特征缩减为更少维数的特征,如下图所示,表示将二维特征缩减为一维特征:
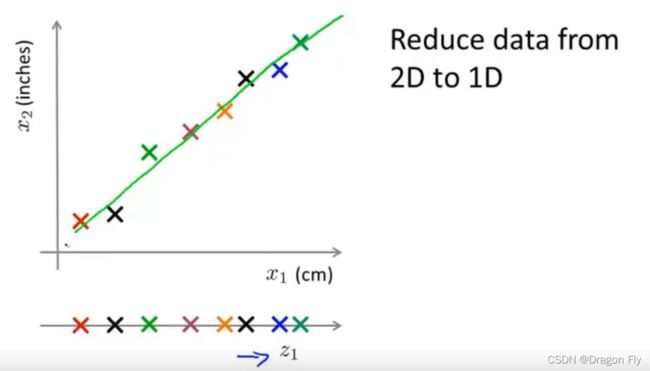
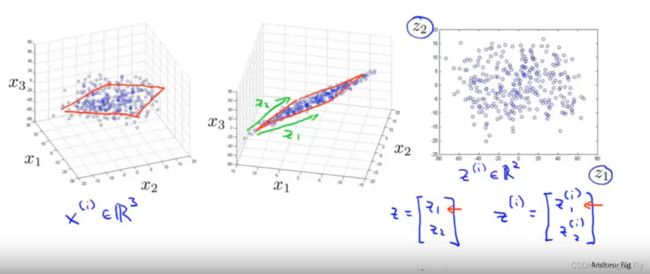
\qquad 下图表示将三维的特征缩减为二维的特征:
3、 主成分分析法-Principal Component Analysis(PCA)
\qquad PCA的目标是为了对数据进行降维,将数据从高维度降到低维度。如若想将二维数据降到一维数据,需要寻找一个方向( u ( 1 ) ∈ R n u^{(1)}\in R^n u(1)∈Rn)来将所有的数据点进行投影,从而最小化投影误差(projection error)。(投影误差指的是将数据垂直投影在某个或某几个向量上,计算投影到向量的距离之和)。若想将n维数据降到k维数据,则需要找k个向量 u ( 1 ) , u ( 2 ) , . . . , u ( k ) u^{(1)}, u^{(2)},...,u^{(k)} u(1),u(2),...,u(k),之后将所有数据投影在这k维数据上,使得投影误差最小。
3.1 数据预处理
\qquad 在进行主成分分析之前,由于数据的量纲不同,通常需要对数据进行预处理,预处理的手段包括feature scaling和mean normalization等。

3.2 PCA流程
\qquad 再将数据进行了预处理之后,首先需要计算数据 X X X的协方差矩阵(Sigma),之后计算协方差矩阵(Sigma)的特征向量 s v d ( S i g m a ) svd(Sigma) svd(Sigma);之后取特征向量中的前k列数据组成新的矩阵 U r e d u c e Ureduce Ureduce;最后计算k维投影向量 z = u r e d u c e ′ ∗ X z = ureduce'*X z=ureduce′∗X

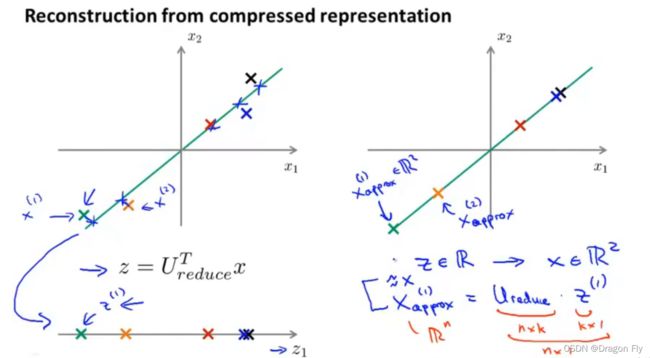
3.3 原始数据重建
\qquad 使用PCA之后,还可以从压缩数据重新转化成为未压缩的数据,因为 z = u r e d u c e ′ ∗ X z = ureduce'*X z=ureduce′∗X,则 X = u r e d u c e ∗ z X = ureduce*z X=ureduce∗z
3.4 主成分数量 k k k的选择
\qquad PCA应用时主成分数量 k k k的选择依据为:选择一个k,使得投影均方误差(下式中的分子)/数据总方差的值不超过0.01,即使得数据的原始方差被保留99%。