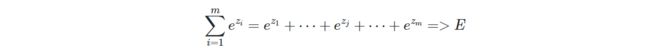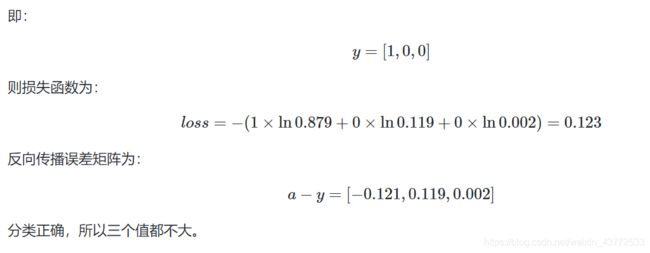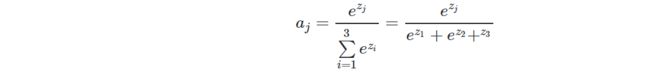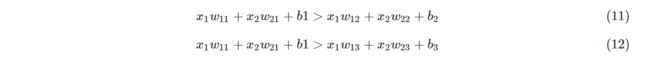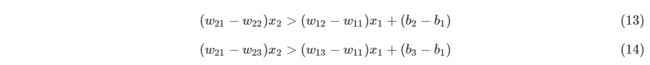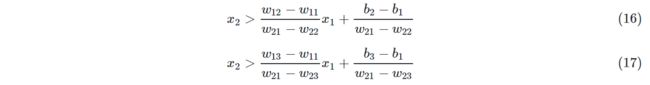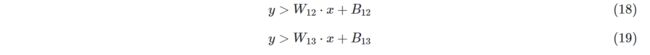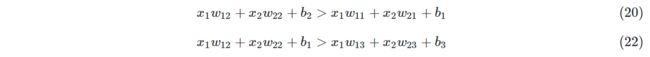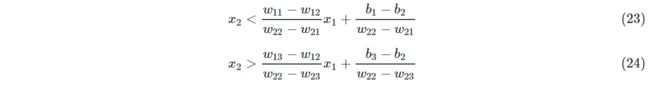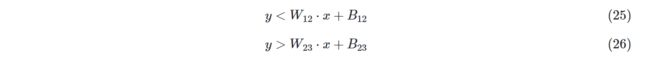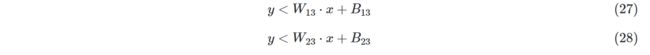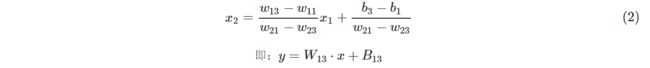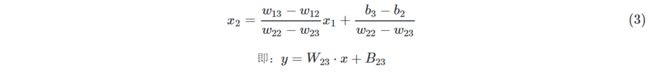神经网络基本原理简明教程之多入多出单层神经网络-线性多分类

一. 线性多分类问题

1 提出问题

我们解决了公元前的楚汉相争的问题，现在看一下公元220年前后的三国问题。

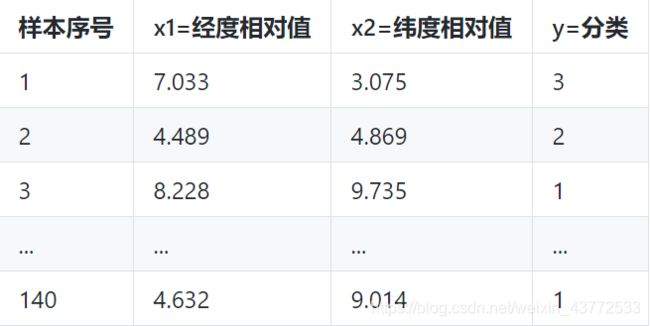
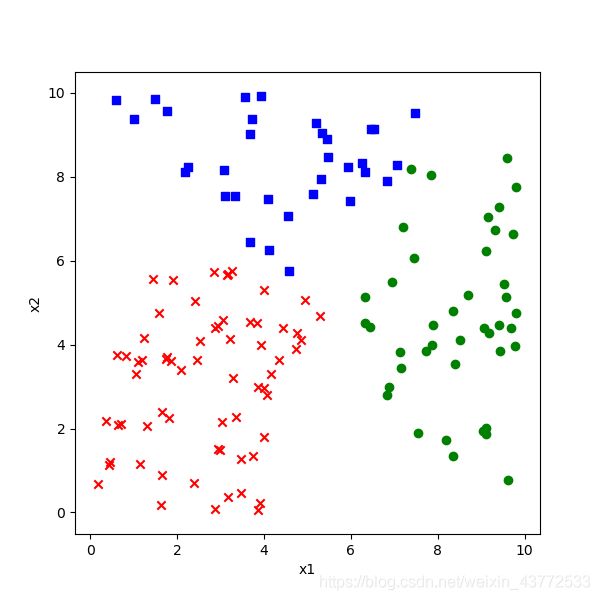
在数据集中一共有140个样本数据，

分类标签值的含义：

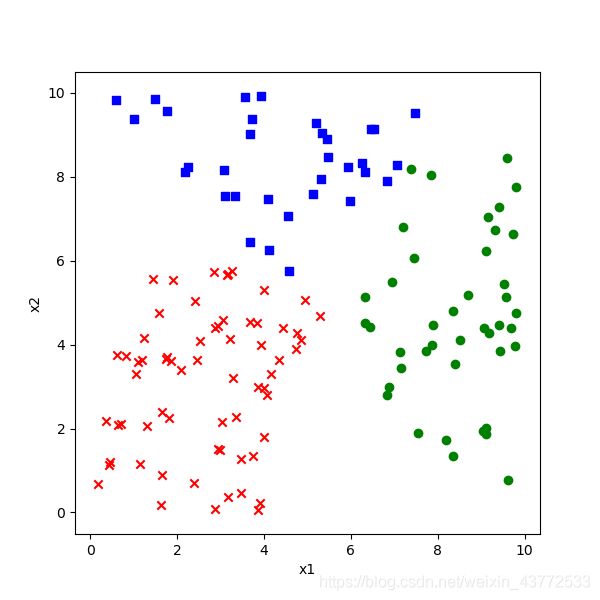
1.魏国城池：标签为1，下图中蓝色点
2.蜀国城池：标签为2，下图中红色点
3.吴国城池：标签为3，下图中绿色点

问题：

1.经纬度相对值为（5,1）时，属于哪个国？
2.经纬度相对值为（7,6）时，属于哪个国？
3.经纬度相对值为（5,6）时，属于哪个国？
4.经纬度相对值为（2,7）时，属于哪个国？

2 多分类学习策略

线性多分类和非线性多分类的区别

下图先示意了线性多分类和非线性多分类的区别：

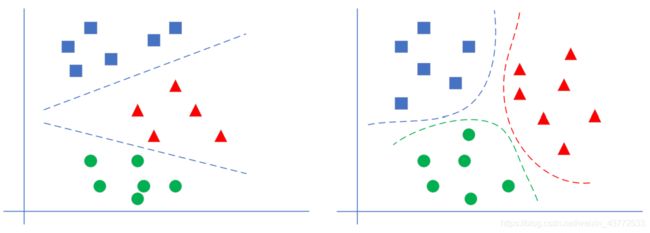
左侧为线性多分类，右侧为非线性多分类。它们的区别在于不同类别的样本点之间是否可以用一条直线来互相分割。对神经网络来说，线性多分类可以使用单层结构来解决，而非线性多分类需要使用双层结构。

二分类与多分类的关系

我们已经学习过了使用神经网络做二分类的方法，它并不能用于多分类。在传统的机器学习中，有些二分类算法可以直接推广到多分类，但是在更多的时候，我们会基于一些基本策略，利用二分类学习器来解决多分类问题。

多分类问题一共有三种解法：

1 一对一
每次先只保留两个类别的数据，训练一个分类器。如果一共有N个类别，则需要训练C2N个分类器。以N=3时举例，需要训练(A|B)，(B|C)，(A|C)三个分类器。

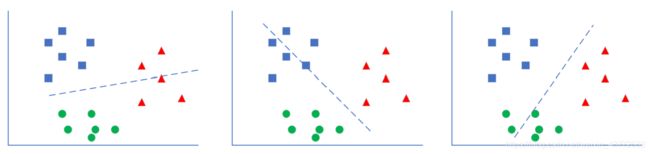
如上图最左侧所示，这个二分类器只关心蓝色和绿色样本的分类，而不管红色样本的情况，也就是说在训练时，只把蓝色和绿色样本输入网络。

推理时，(A|B)分类器告诉你是A类时，需要到(A|C)分类器再试一下，如果也是A类，则就是A类。如果(A|C)告诉你是C类，则基本是C类了，不可能是B类，不信的话可以到(B|C)分类器再去测试一下。

2. 一对多
   如下图，处理一个类别时，暂时把其它所有类别看作是一类，这样对于三分类问题，可以得到三个分类器。

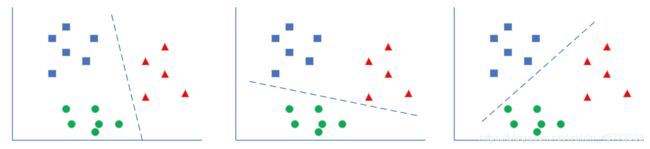
如最左图，这种情况是在训练时，把红色样本当作一类，把蓝色和绿色样本混在一起当作另外一类。

推理时，同时调用三个分类器，再把三种结果组合起来，就是真实的结果。比如，第一个分类器告诉你是“红类”，那么它确实就是红类；如果告诉你是非红类，则需要看第二个分类器的结果，绿类或者非绿类；依此类推。

3 多对多
假设有4个类别ABCD，我们可以把AB算作一类，CD算作一类，训练一个分类器1；再把AC算作一类，BD算作一类，训练一个分类器2。

推理时，第1个分类器告诉你是AB类，第二个分类器告诉你是BD类，则做“与”操作，就是B类。

多分类与多标签

多分类学习中，虽然有多个类别，但是每个样本只属于一个类别。

有一种情况也很常见，比如一幅图中，既有蓝天白云，又有花草树木，那么这张图片可以有两种标注方法：

1.标注为“风景”，而不是“人物”，属于风景图片，这叫做分类
2.被同时标注为“蓝天”、“白云”、“花草”、“树木”等多个标签，这样的任务不叫作多分类学习，而是“多标签”学习，multi-label learning。我们此处不涉及这类问题。

二. 多分类问题

此函数对线性多分类和非线性多分类都适用。

先回忆一下二分类问题，在线性计算后，使用了Logistic函数计算样本的概率值，从而把样本分成了正负两类。那么对于多分类问题，应该使用什么方法来计算样本属于各个类别的概率值呢？又是如何作用到反向传播过程中的呢？我们这一节主要研究这个问题。’

1 多分类函数定义 - Softmax

为什么叫做Softmax？
假设输入值是：[3,1,-3]，如果取max操作会变成：[1,0,0]，这符合我们的分类需要。但是有两个不足：

1.分类结果是[1，0，0]，只保留的非0即1的信息，没有各元素之间相差多少的信息，可以理解是“Hard-Max”
2.max操作本身不可导，无法用在反向传播中。
所以Softmax加了个"soft"来模拟max的行为，但同时又保留了相对大小的信息。

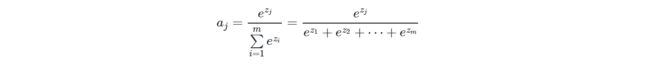
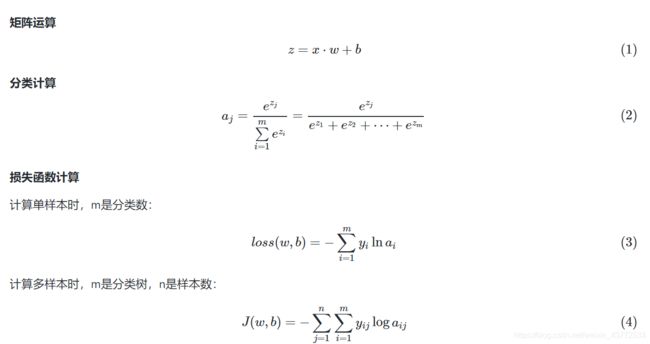
上式中:

1.zj是对第 j 项的分类原始值，即矩阵运算的结果
2.zi是参与分类计算的每个类别的原始值
3.m 是总的分类数
4.aj是对第 j 项的计算结果

假设j=1，m=3，上式为：

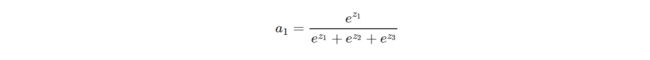
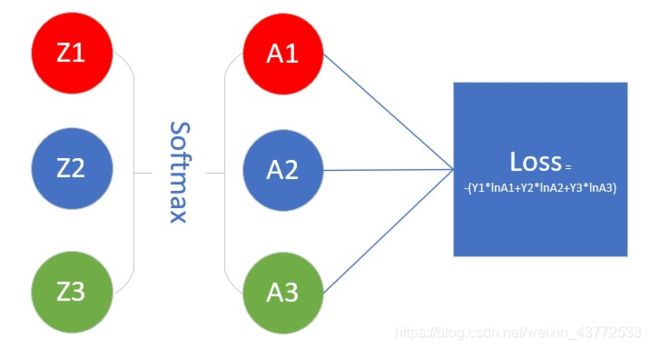
用一张图来形象地说明这个过程：

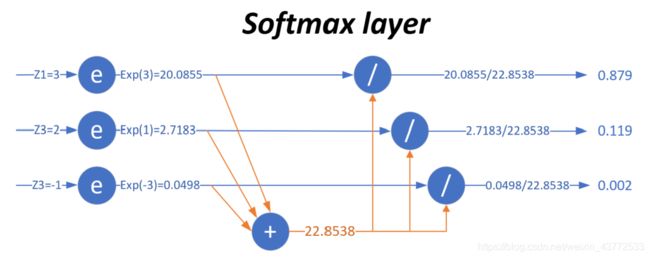
当输入的数据[z1,z2,z3]是[3,1,−3]时，按照图示过程进行计算，可以得出输出的概率分布是[0.879,0.119,0.002]。

总结一下：

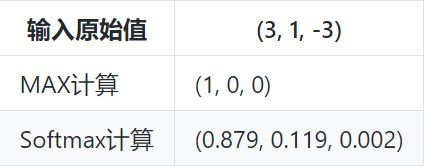
也就是说，在（至少）有三个类别时，通过使用Softmax公式计算它们的输出，比较相对大小后，得出该样本属于第一类，因为第一类的值为0.879，在三者中最大。注意这是对一个样本的计算得出的数值，而不是三个样本，亦即softmax给出了某个样本分别属于三个类别的概率。

它有两个特点：

1.三个类别的概率相加为1
2.每个类别的概率都大于0

Softmax的工作原理

我们仍假设网络输出的预测数据是z=[3, 1, -3]，而标签值是y=[1, 0, 0]。在做反向传播时，根据前面的经验，我们会用z-y，得到：

这个信息很奇怪：

第一项是2，我们已经预测准确了此样本属于第一类，但是反向误差的值是2，即惩罚值是2
第二项是1，惩罚值是1，预测对了，仍有惩罚值
第三项是-3，惩罚值是-3，意为着奖励值是3，明明预测错误了却给了奖励

所以，如果不使用Softmax这种机制，会存在有个问题：

z值和y值之间，即预测值和标签值之间不可比，比如z[0]=3与y[0]=1是不可比的
z值中的三个元素之间虽然可比，但只能比大小，不能比差值，比如z[0]>z[1]>z[2]，但3和1相差2，1和-3相差4，这些差值是无意义的

在使用Softmax之后，我们得到的值是a=[0.879, 0.119, 0.002]，用a-y：

再来分析这个信息：

第一项-0.121是奖励给该类别0.121，因为它做对了，但是可以让这个概率值更大，最好是1

第二项0.119是惩罚，因为它试图给第二类0.119的概率，所以需要这个概率值更小，最好是0

第三项0.002是惩罚，因为它试图给第三类0.002的概率，所以需要这个概率值更小，最好是0

这个信息是完全正确的，可以用于反向传播。Softmax先做了归一化，把输出值归一到[0,1]之间，这样就可以与标签值的0或1去比较，并且知道惩罚或奖励的幅度。

从继承关系的角度来说，Softmax函数可以视作Logistic函数扩展，比如一个二分类问题：

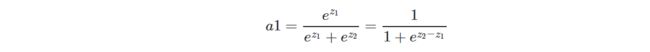
是不是和Logistic函数形式非常像？其实Logistic函数也是给出了当前样本的一个概率值，只不过是依靠偏近0或偏近1来判断属于正类还是负类。

2 正向传播

图示如下：

3 反向传播

实例化推导

我们先用实例化的方式来做反向传播公式的推导，然后再扩展到一般性上。假设有三个类别，则：

为了方便书写，我们令：

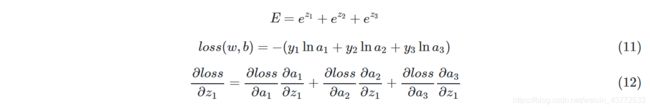
依次求解公式12中的各项：

把公式13~18组合到12中：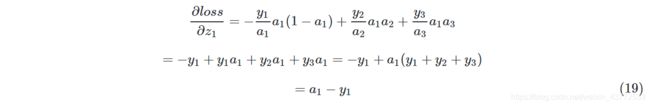
不失一般性，由公式19可得：

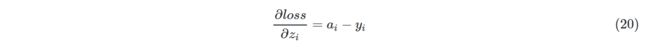
一般性推导

1.Softmax函数自身的求导
由于Softmax涉及到求和，所以有两种情况：

求输出项a1对输入项z1的导数，此时：j=1,i=1,i=j，可以扩展到i, j为任意相等值

求输出项a2或a3对输入项z1的导数，此时：j=2或3,i=1,i≠j，可以扩展到i, j为任意不等值

Softmax函数的分子：因为是计算aj，所以分子是ezj。

Softmax函数的分母：

2. 结合损失函数的整体反向传播公式

看上图，我们要求Loss值对Z1的偏导数。和以前的Logistic函数不同，那个函数是一个z对应一个a，所以反向关系也是一对一。而在这里，a1的计算是有z1,z2,z3参与的，a2的计算也是有z1,z2,z3参与的，即所有a的计算都与前一层的z有关，所以考虑反向时也会比较复杂。

先从Loss的公式看，loss=−(y1lna1+y2lna2+y3lna3)，a1肯定与z1有关，那么a2,a3是否与z1有关呢？

再从Softmax函数的形式来看：

无论是a1，a2，a3，都是与z1相关的，而不是一对一的关系，所以，想求Loss对Z1的偏导，必须把Loss->A1->Z1， Loss->A2->Z1，Loss->A3->Z1，这三条路的结果加起来。于是有了如下公式：

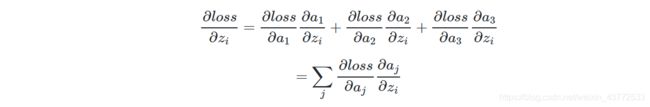
你可以假设上式中i=1，j=3，就完全符合我们的假设了，而且不失普遍性。

前面说过了，因为Softmax涉及到各项求和，A的分类结果和Y的标签值分类是否一致，所以需要分情况讨论：

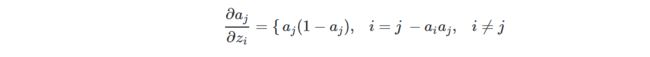
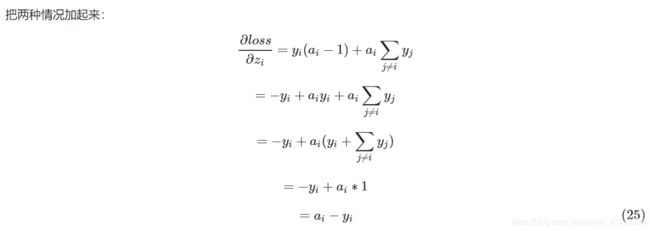
因为yj是取值[1,0,0]或者[0,1,0]或者[0,0,1]的，这三者用∑加起来，就是[1,1,1]，在矩阵乘法运算里乘以[1,1,1]相当于什么都不做，就等于原值。

我们惊奇地发现，最后的反向计算过程就是：ai−yi，假设当前样本的ai=[0.879,0.119,0.002]，而yi=[0,1,0]，则：

ai−yi=[0.879,0.119,0.002]−[0,1,0]=[0.879,−0.881,0.002]
其含义是，样本预测第一类，但实际是第二类，所以给第一类0.879的惩罚值，给第二类0.881的奖励，给第三类0.002的惩罚，并反向传播给神经网络。

后面对z=wx+b的求导，与二分类一样，不再赘述。

Softmax函数的Python实现

第一种，直截了当按照公式写：

def Softmax1(x):
    e_x = np.exp(x)
    v = np.exp(x) / np.sum(e_x)
    return v

这个可能会发生的问题是，当x很大时，np.exp(x)很容易溢出，因为是指数运算。所以，有了下面这种改进的代码：

def Softmax2(Z):
    shift_Z = Z - np.max(Z)
    exp_Z = np.exp(shift_Z)
    A = exp_Z / np.sum(exp_Z)
    return A

测试一下：

Z = np.array([3,0,-3])
print(Softmax1(Z))
print(Softmax2(Z))

两个实现方式的结果一致：

[0.95033021 0.04731416 0.00235563]
[0.95033021 0.04731416 0.00235563]

为什么一样呢？从代码上看差好多啊！我们来证明一下：

假设有3个值a，b，c，并且a在三个数中最大，则b所占的Softmax比重应该这样写：

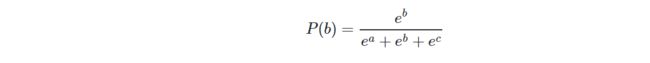
如果减去最大值变成了a-a，b-a，c-a，则b’所占的Softmax比重应该这样写:

Softmax2的写法对一个一维的向量或者数组是没问题的，如果遇到Z是个MxN维(M,N>1)的矩阵的话，就有问题了，因为

np.sum(exp_Z)这个函数，会把MxN矩阵里的所有元素加在一起，得到一个标量值，而不是相关列元素加在一起。

所以应该这么写：

class Softmax(object):
    def forward(self, z):
        shift_z = z - np.max(z, axis=1, keepdims=True)
        exp_z = np.exp(shift_z)
        a = exp_z / np.sum(exp_z, axis=1, keepdims=True)
        return a

axis=1这个参数非常重要，因为如果输入Z是单样本的预测值话，如果是分三类，则应该是个3x1的数组，如果：

z=[3,1,−3]
a=[0.879,0.119,0.002]

但是，如果是批量训练，假设每次用两个样本，则：

if __name__ == '__main__':
    z = np.array([[3,1,-3],[1,-3,3]]).reshape(2,3)
    a = Softmax().forward(z)
    print(a)

结果：

[[0.87887824 0.11894324 0.00217852]
 [0.11894324 0.00217852 0.87887824]]

其中，a是包含两个样本的softmax结果，每个数组里面的三个数字相加为1。

如果s = np.sum(exp_z)，不指定axis=1参数，则：

[[0.43943912 0.05947162 0.00108926]
 [0.05947162 0.00108926 0.43943912]]

A虽然仍然包含两个样本，但是变成了两个样本所有的6个元素相加为1，这不是softmax的本意，softmax只计算一个样本（一行）中的数据。

三 线性多分类的神经网络实现

1 定义神经网络结构

从图示来看，似乎在三个颜色区间之间有两个比较明显的分界线，而且是直线，即线性可分的。我们如何通过神经网络精确地找到这两条分界线呢？

·1.从视觉上判断是线性可分的，所以我们使用单层神经网络即可

2.输入特征是两个，X1=经度，X2=纬度

3.最后输出的是三个分类，分别是魏蜀吴，所以输出层有三个神经元

如果有三个以上的分类同时存在，我们需要对每一类别分配一个神经元，这个神经元的作用是根据前端输入的各种数据，先做线性处理（Y=WX+B)，然后做一次非线性处理，计算每个样本在每个类别中的预测概率，再和标签中的类别比较，看看预测是否准确，如果准确，则奖励这个预测，给与正反馈；如果不准确，则惩罚这个预测，给与负反馈。两类反馈都反向传播到神经网络系统中去调整参数。

这个网络只有输入层和输出层，由于输入层不算在内，所以是一层网络。

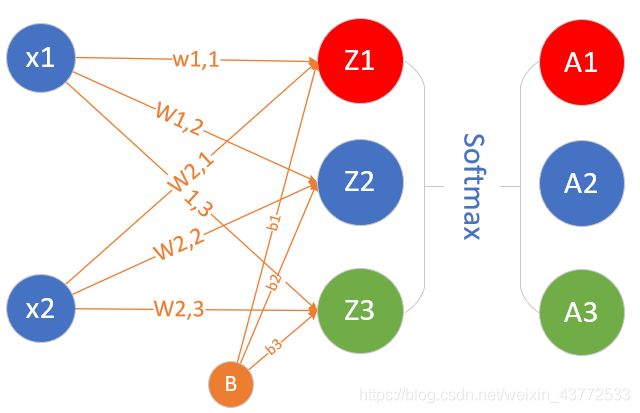
与前面的单层网络不同的是，本图最右侧的输出层还多出来一个Softmax分类函数，这是多分类任务中的标准配置，可以看作是输出层的激活函数，并不单独成为一层，与二分类中的Logistic函数一样。

2 样本数据

使用SimpleDataReader类读取数据后，观察一下数据的基本属性：

reader.XRaw.shape
(140, 2)
reader.XRaw.min()
0.058152279749505986
reader.XRaw.max()
9.925126526921046

reader.YRaw.shape
(140, 1)
reader.YRaw.min()
1.0
reader.YRaw.max()
3.0

训练数据X，140个记录，两个特征，最小值0.058，最大值9.925
标签数据Y，140个记录，一个分类值，取值范围是[1,2,3]

样本标签数据

一般来说，在标记样本时，我们会用1，2，3这样的标记，来指明是哪一类。所以样本数据中是这个样子的：

Y=(y1 y2 … y140)=(32…1)

在有Softmax的多分类计算时，我们用下面这种等价的方式，俗称One-Hot，就是在一个向量中只有一个数据是1，其它都是0。

Y=(y1 y2 … y140)=(001 010 … 100)

OneHot的意思，在这一列数据中，只有一个1，其它都是0。1所在的列数就是这个样本的分类类别。

标签数据对应到每个样本数据上，列对齐，只有(1,0,0)，(0,1,0)，(0,0,1)三种组合，分别表示第一类、第二类和第三类。

在SimpleDataReader中实现ToOneHot()方法，把原始标签转变成One-Hot编码：

class SimpleDataReader(object):
    def ToOneHot(self, num_category, base=0):
        count = self.YRaw.shape[0]
        self.num_category = num_category
        y_new = np.zeros((count, self.num_category))
        for i in range(count):
            n = (int)(self.YRaw[i,0])
            y_new[i,n-base] = 1

3 代码实现

添加分类函数

在Activators.py中，增加Softmax的实现，并添加单元测试。

class Softmax(object):
    def forward(self, z):
        shift_z = z - np.max(z, axis=1, keepdims=True)
        exp_z = np.exp(shift_z)
        a = exp_z / np.sum(exp_z, axis=1, keepdims=True)
        return a

if __name__ == '__main__':
    z = np.array([[3,1,-3],[1,-3,3]]).reshape(2,3)
    a = Softmax().forward(z)
    print(a)        

前向计算

前向计算需要增加分类函数调用：

class NeuralNet(object):
    def forwardBatch(self, batch_x):
        Z = np.dot(batch_x, self.W) + self.B
        if self.params.net_type == NetType.BinaryClassifier:
            A = Logistic().forward(Z)
            return A
        elif self.params.net_type == NetType.MultipleClassifier:
            A = Softmax().forward(Z)
            return A
        else:
            return Z

反向传播

在多分类函数一节详细介绍了反向传播的推导过程，推导的结果很令人惊喜，就是一个简单的减法，与前面学习的拟合、二分类的算法结果都一样。

class NeuralNet(object):
    def backwardBatch(self, batch_x, batch_y, batch_a):
        m = batch_x.shape[0]
        dZ = batch_a - batch_y
        dB = dZ.sum(axis=0, keepdims=True)/m
        dW = np.dot(batch_x.T, dZ)/m
        return dW, dB

计算损失函数值

损失函数不再是均方差和二分类交叉熵了，而是交叉熵函数对于多分类的形式，并且添加条件分支来判断只在网络类型为多分类时调用此损失函数。

class LossFunction(object):
    # fcFunc: feed forward calculation
    def CheckLoss(self, A, Y):
        m = Y.shape[0]
        if self.net_type == NetType.Fitting:
            loss = self.MSE(A, Y, m)
        elif self.net_type == NetType.BinaryClassifier:
            loss = self.CE2(A, Y, m)
        elif self.net_type == NetType.MultipleClassifier:
            loss = self.CE3(A, Y, m)
        #end if
        return loss
    # end def

    # for multiple classifier
    def CE3(self, A, Y, count):
        p1 = np.log(A)
        p2 =  np.multiply(Y, p1)
        LOSS = np.sum(-p2) 
        loss = LOSS / count
        return loss
    # end def

推理函数

def inference(net, reader):
    xt_raw = np.array([5,1,7,6,5,6,2,7]).reshape(4,2)
    xt = reader.NormalizePredicateData(xt_raw)
    output = net.inference(xt)
    r = np.argmax(output, axis=1)+1
    print("output=", output)
    print("r=", r)

注意在推理之前，先做了归一化，因为原始数据是在[0,10]范围的。

函数np.argmax的作用是比较output里面的几个数据的值，返回最大的那个数据的行数或者列数，0-based。比如ouput=(1.02,-3,2.2)时，会返回2，因为2.2最大，所以我们再加1，把返回值变成[1，2，3]的其中一个。

np.argmax函数的参数axis=1，是因为有4个样本参与预测，所以需要在第二维上区分开来，分别计算每个样本的argmax值。

if __name__ == '__main__':
    num_category = 3
    reader = SimpleDataReader()
    reader.ReadData()
    reader.NormalizeX()
    reader.ToOneHot(num_category, base=1)

    num_input = 2
    params = HyperParameters(num_input, num_category, eta=0.1, max_epoch=100, batch_size=10, eps=1e-3, net_type=NetType.MultipleClassifier)
    net = NeuralNet(params)
    net.train(reader, checkpoint=1)

    inference(net, reader)

4 运行结果

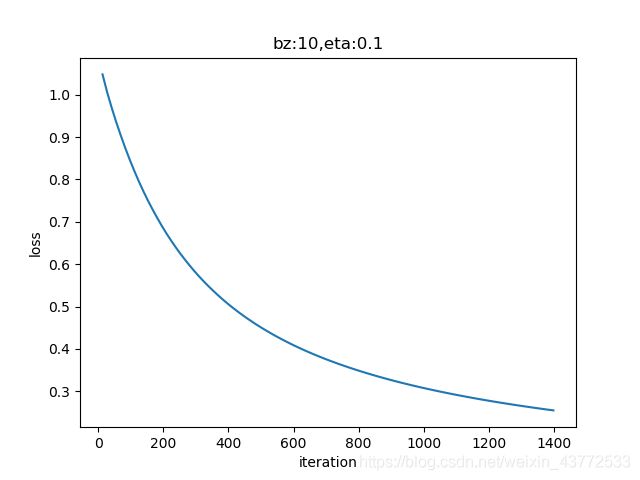
损失函数历史记录

从趋势上来看，loss值还有进一步下降的可能，以提高模型精度。有兴趣的读者可以多训练几轮，看看效果。

下面是打印输出的最后几行：

epoch=97
97 13 0.25785892951858186
epoch=98
98 13 0.25640075114165223
epoch=99
99 13 0.25497053433985734
W= [[-1.43234109 -3.57409342  5.00643451]
 [ 4.47791288 -2.88936887 -1.58854401]]
B= [[-1.81896724  3.66606162 -1.84709438]]
output= [[0.01801124 0.73435241 0.24763634]
 [0.24709055 0.15438074 0.59852871]
 [0.38304995 0.37347646 0.24347359]
 [0.51360269 0.46266935 0.02372795]]
r= [2 3 1 1]

注意，output的结果，对于每个测试样本的结果，是按行看的，即第一行是第一个测试样本的分类结果。

经纬度相对值为(5,1)时，概率0.734最大，属于2，蜀国
经纬度相对值为(7,6)时，概率0.598最大，属于3，吴国
经纬度相对值为(5,6)时，概率0.383最大，属于1，魏国
经纬度相对值为(2,7)时，概率0.513最大，属于1，魏国

完整代码：

获取HelperClass包请扫描下面的二维码：

获取数据集请扫描下面二维码：

import numpy as np

from HelperClass.NeuralNet_1_2 import *

file_name = "ch07.npz"

def inference(net, reader):
    xt_raw = np.array([5,1,7,6,5,6,2,7]).reshape(4,2)
    xt = reader.NormalizePredicateData(xt_raw)
    output = net.inference(xt)
    r = np.argmax(output, axis=1)+1
    print("output=", output)
    print("r=", r)

# 主程序
if __name__ == '__main__':
    num_category = 3
    reader = DataReader_1_3(file_name)
    reader.ReadData()
    reader.NormalizeX()
    reader.ToOneHot(num_category, base=1)

    num_input = 2
    params = HyperParameters_1_1(num_input, num_category, eta=0.1, max_epoch=100, batch_size=10, eps=1e-3, net_type=NetType.MultipleClassifier)
    net = NeuralNet_1_2(params)
    net.train(reader, checkpoint=1)

    inference(net, reader)

三 线性多分类原理

此原理对线性多分类和非线性多分类都适用。

1 多分类过程

我们在此以具有两个特征值的三分类举例。可以扩展到更多的分类或任意特征值，比如在ImageNet的图像分类任务中，最后一层全连接层输出给分类器的特征值有成千上万个，分类有1000个。

2 数值计算举例

如果标签值表明是此样本为第一类

如果标签值表明是此样本为第二类

3 多分类的几何原理

在前面的二分类原理中，很容易理解为我们用一条直线分开两个部分。对于多分类问题，是否可以沿用二分类原理中的几何解释呢？答案是肯定的，只不过需要单独判定每一个类别。

如上图，假设一共有三类样本，蓝色为1，红色为2，绿色为3，那么Softmax的形式应该是：

当样本属于第一类时
把蓝色点与其它颜色的点分开。

如果判定一个点属于第一类，则a1的概率值一定会比a2、a3大，表示为公式：

由于Softmax的特殊形式，分母都一样，所以只比较分子就行了。而分子是一个自然指数，输出值域大于零且单调递增，所以只比较指数就可以了，因此，公式9等同于下式：

把公式1、2、3引入到10：

变形：

我们先假设：

所以公式13、14左侧的系数都大于零，两边同时除以系数：

简化：

此时y代表了第一类的蓝色点。

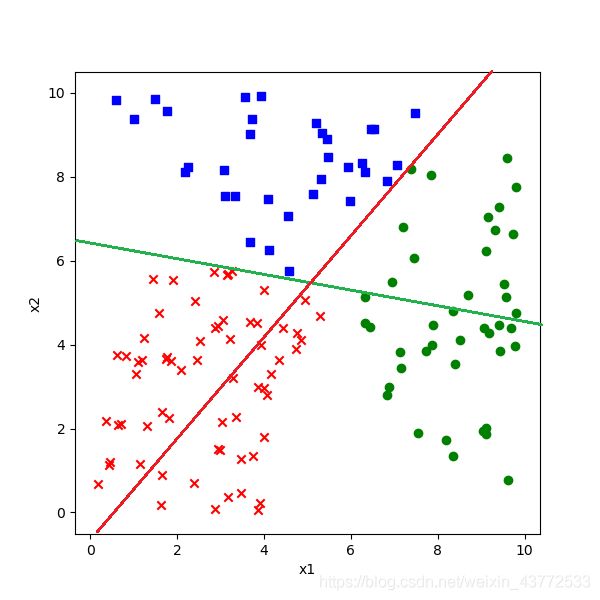
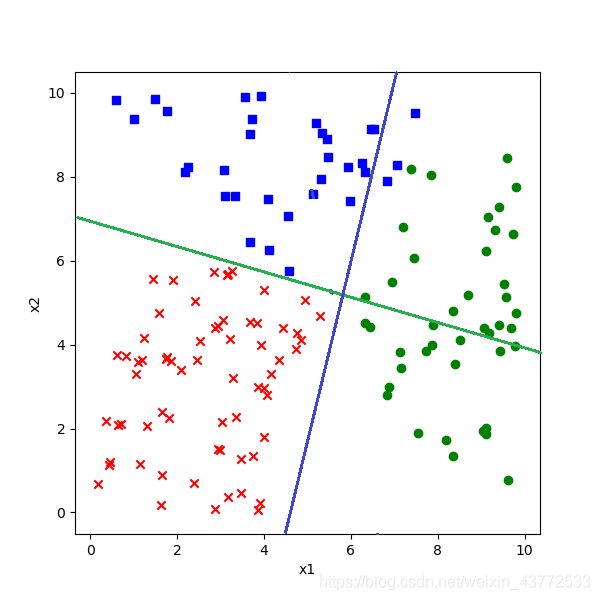
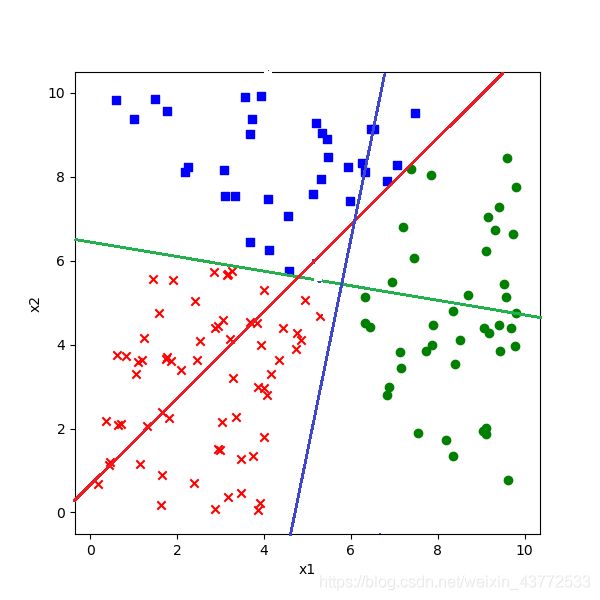
借用二分类中的概念，公式18的几何含义是：有一条直线可以分开第一类（蓝色点）和第二类（红色点），使得所有蓝色点都在直线的上方，所有的红色点都在直线的下方。于是我们可以画出下图中的那条绿色直线。

而公式19的几何含义是：有一条直线可以分开第一类（蓝色点）和第三类（绿色点），使得所有蓝色点都在直线的上方，所有的绿色点都在直线的下方。于是我们可以画出下图中的那条红色直线。

也就是说在图中画两条直线，所有红点都同时在红线和绿线这两条直线的上方，即蓝色点的区域。如下图所示：

当样本属于第二类时

把红色点与其它两色点分开。

则：

仍然用公式15的假设：

两边除以相同的系数后，不等号会有变化：

对比公式16和公式23，由于：

所以：

此时y代表了第二类的红色点。

公式25和公式18几何含义相同，不等号相反，代表了下图中绿色直线的分割作用，即红色点在绿色直线下方。

公式26的几何含义是，有一条直线可以分开第二类（红色点）和第三类（绿色点），使得所有红色点都在直线的上方，所有的绿色点都在直线的下方。于是我们可以画出下图中的那条蓝色直线的分割作用。

当样本属于第三类时

把绿色点与其它两色点分开。

最后可得：

此时y代表了第三类的绿色点。

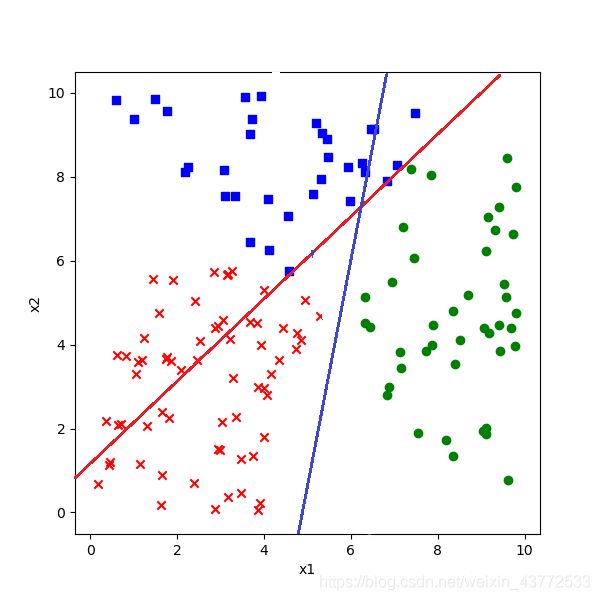
公式27与公式19不等号相反，几何含义相同，代表了下图中红色直线的分割作用，绿色点在红色直线下方。

公式28与公式26不等号相反，几何含义相同，代表了下图中蓝色直线的分割作用，绿色点在蓝色直线下方。

把三张图综合在一起，应该是这个样子：

四 多分类结果可视化

神经网络到底是一对一方式，还是一对多方式呢？从Softmax公式，好像是一对多方式，因为只取一个最大值，那么理想中的一对多方式应该是：

实际上是什么样子的，我们来看下面的具体分析。

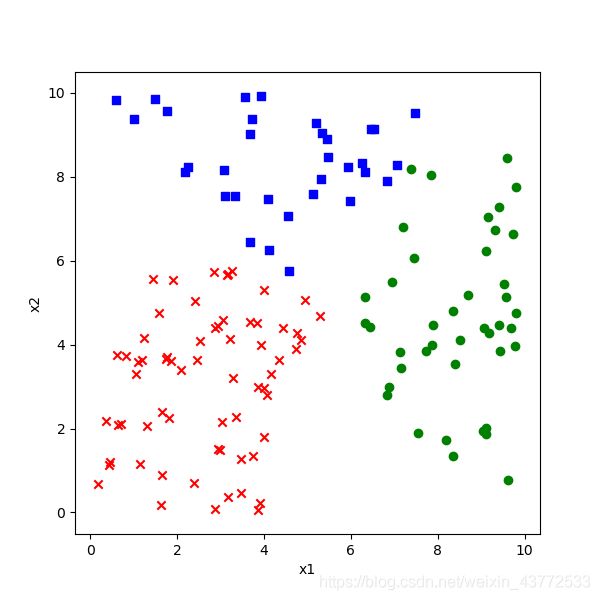
1 显示原始数据图

与二分类时同样的问题，如何直观地理解多分类的结果？三分类要复杂一些，我们先把原始数据显示出来。

def ShowData(X,Y):
    for i in range(X.shape[0]):
        if Y[i,0] == 1:
            plt.plot(X[i,0], X[i,1], '.', c='r')
        elif Y[i,0] == 2:
            plt.plot(X[i,0], X[i,1], 'x', c='g')
        elif Y[i,0] == 3:
            plt.plot(X[i,0], X[i,1], '^', c='b')
        # end if
    # end for
    plt.show()

会画出下面这张图：

2 显示分类结果分割线图

下面的数据是神经网络训练出的权重和偏移值的结果：

......
epoch=98
98 1385 0.25640040547970516
epoch=99
99 1399 0.2549651316913006
W= [[-1.43299777 -3.57488388  5.00788165]
 [ 4.47527075 -2.88799216 -1.58727859]]
B= [[-1.821679    3.66752583 -1.84584683]]
......

公式16，把不等号变成等号，即z1=z2，则代表了那条绿色的分割线，用于分割第一类和第二类的：

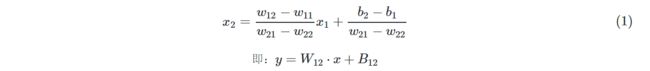
由于Python数组是从0开始的，所以公式1中的所有下标都减去1，写成代码：

b12 = (net.B[0,1] - net.B[0,0])/(net.W[1,0] - net.W[1,1])
w12 = (net.W[0,1] - net.W[0,0])/(net.W[1,0] - net.W[1,1])

公式17，把不等号变成等号，即z1=z3，则代表了那条红色的分割线，用于分割第一类和第三类的：

写成代码：

b13 = (net.B[0,0] - net.B[0,2])/(net.W[1,2] - net.W[1,0])
w13 = (net.W[0,0] - net.W[0,2])/(net.W[1,2] - net.W[1,0])

公式24，把不等号变成等号，即z2=z3，则代表了那条蓝色的分割线，用于分割第二类和第三类的：

写成代码：

b23 = (net.B[0,2] - net.B[0,1])/(net.W[1,1] - net.W[1,2])
w23 = (net.W[0,2] - net.W[0,1])/(net.W[1,1] - net.W[1,2])

完整代码如下：

def ShowResult(net,X,Y,xt):
    for i in range(X.shape[0]):
        category = np.argmax(Y[i])
        if category == 0:
            plt.plot(X[i,0], X[i,1], '.', c='r')
        elif category == 1:
            plt.plot(X[i,0], X[i,1], 'x', c='g')
        elif category == 2:
            plt.plot(X[i,0], X[i,1], '^', c='b')
        # end if
    # end for

    b13 = (net.B[0,0] - net.B[0,2])/(net.W[1,2] - net.W[1,0])
    w13 = (net.W[0,0] - net.W[0,2])/(net.W[1,2] - net.W[1,0])

    b23 = (net.B[0,2] - net.B[0,1])/(net.W[1,1] - net.W[1,2])
    w23 = (net.W[0,2] - net.W[0,1])/(net.W[1,1] - net.W[1,2])

    b12 = (net.B[0,1] - net.B[0,0])/(net.W[1,0] - net.W[1,1])
    w12 = (net.W[0,1] - net.W[0,0])/(net.W[1,0] - net.W[1,1])

    x = np.linspace(0,1,2)
    y = w13 * x + b13
    p13, = plt.plot(x,y,c='g')

    x = np.linspace(0,1,2)
    y = w23 * x + b23
    p23, = plt.plot(x,y,c='r')

    x = np.linspace(0,1,2)
    y = w12 * x + b12
    p12, = plt.plot(x,y,c='b')

    plt.legend([p13,p23,p12], ["13","23","12"])

    for i in range(xt.shape[0]):
        plt.plot(xt[i,0], xt[i,1], 'o')

    plt.axis([-0.1,1.1,-0.1,1.1])
    plt.show()

改一下主函数，增加对以上两个函数ShowData()和ShowResult()的调用：

if __name__ == '__main__':
    num_category = 3
    reader = SimpleDataReader()
    reader.ReadData()

    ShowData(reader.XRaw, reader.YRaw)

    reader.NormalizeX()
    reader.ToOneHot(num_category, base=1)

    num_input = 2
    params = HyperParameters(num_input, num_category, eta=0.1, max_epoch=100, batch_size=10, eps=1e-3, net_type=NetType.MultipleClassifier)
    net = NeuralNet(params)
    net.train(reader, checkpoint=1)

    xt_raw = np.array([5,1,7,6,5,6,2,7]).reshape(4,2)
    xt = reader.NormalizePredicateData(xt_raw)
    output = net.inference(xt)
    print(output)

    ShowResult(net, reader.XTrain, reader.YTrain, xt)

最后可以看到这样的分类结果图，注意，这个结果图和我们在7.2中分析的一样，只是蓝线斜率不同：

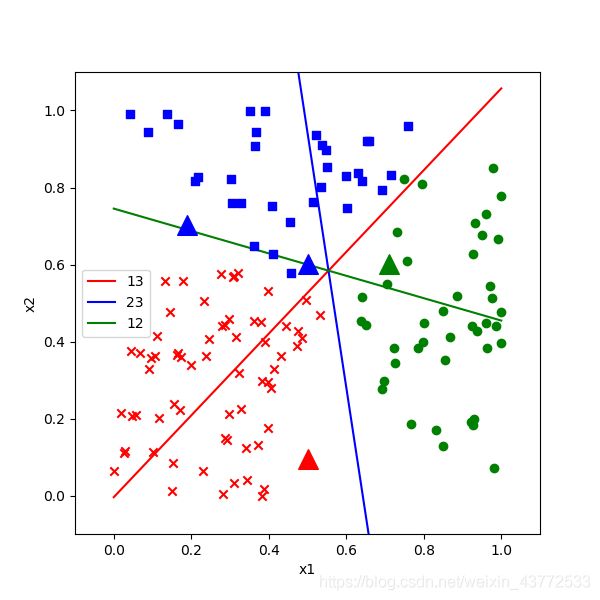
上图中的四个圆形的点是需要我们预测的四个坐标值，其中三个点的分类都比较明确，只有那个绿色的点看不清楚在边界那一侧，可以通过在实际的运行结果图上放大局部来观察。

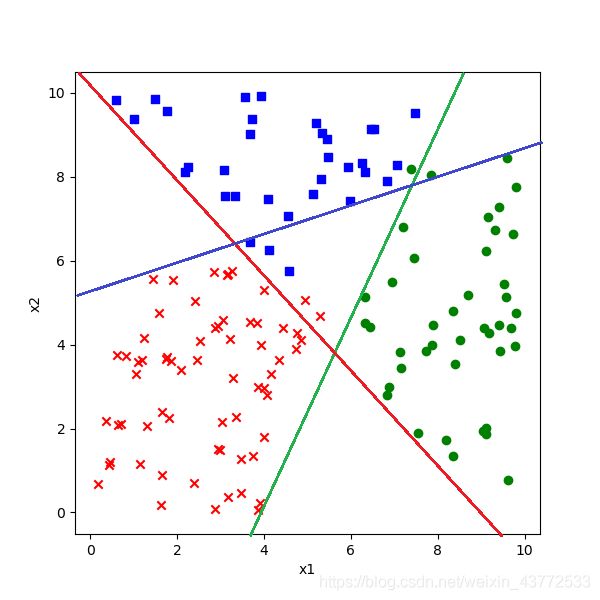
3 理解神经网络的分类方式

上图中：

蓝色线是2|3的边界，不考虑第1类
绿色线是1|2的边界，不考虑第3类
红色线是1|3的边界，不考虑第2类

我们只看蓝色的第1类，当要区分1|2和1|3时，神经网络实际是用了两条直线（绿色和红色）同时作为边界。那么它是一对一方式还是一对多方式呢？

程序的输出图上的分割线是我们令z1=z2, z2=z3, z3=z1三个等式得到的，但实际上神经网络的工作方式不是这样的，它不会单独比较两类，而是会同时比较三类，这个从Softmax会同时输出三个概率值就可以理解。比如，当我们想得到第一类的分割线时，需要同时满足两个条件：

即，找到第一类和第二类的边界，同时，找到第一类和第三类的边界。

这就意味着公式4其实是一个线性分段函数，而不是两条直线，即下图中红色射线和绿色射线所组成的函数。

同理，用于分开红色点和其它两类的分割线是蓝色射线和绿色射线，用于分开绿色点和其它两类的分割线是红色射线和蓝色射线。

训练一对多分类器时，是把蓝色样本当作一类，把红色和绿色样本混在一起当作另外一类。训练一对一分类器时，是把绿色样本扔掉，只考虑蓝色样本和红色样本。而神经网络并非以上两种方式。而我们在此并没有这样做，三类样本是同时参与训练的。所以我们只能说神经网络从结果上看，是一种一对多的方式，至于它的实质，我们在后面的非线性分类时再进一步探讨。

完整代码：

import numpy as np
import matplotlib.pyplot as plt
from pathlib import Path
import math

from HelperClass.NeuralNet_1_2 import *
from HelperClass.Visualizer_1_0 import *

file_name = "ch07.npz"

def ShowData(X,Y):
    fig = plt.figure(figsize=(6,6))
    DrawThreeCategoryPoints(X[:,0], X[:,1], Y[:], xlabel="x1", ylabel="x2", show=True)

def ShowResult(X,Y,xt,yt):
    fig = plt.figure(figsize=(6,6))
    DrawThreeCategoryPoints(X[:,0], X[:,1], Y[:], xlabel="x1", ylabel="x2", show=False)

    b13 = (net.B[0,0] - net.B[0,2])/(net.W[1,2] - net.W[1,0])
    w13 = (net.W[0,0] - net.W[0,2])/(net.W[1,2] - net.W[1,0])

    b23 = (net.B[0,2] - net.B[0,1])/(net.W[1,1] - net.W[1,2])
    w23 = (net.W[0,2] - net.W[0,1])/(net.W[1,1] - net.W[1,2])

    b12 = (net.B[0,1] - net.B[0,0])/(net.W[1,0] - net.W[1,1])
    w12 = (net.W[0,1] - net.W[0,0])/(net.W[1,0] - net.W[1,1])

    x = np.linspace(0,1,2)
    y = w13 * x + b13
    p13, = plt.plot(x,y,c='r')

    x = np.linspace(0,1,2)
    y = w23 * x + b23
    p23, = plt.plot(x,y,c='b')

    x = np.linspace(0,1,2)
    y = w12 * x + b12
    p12, = plt.plot(x,y,c='g')

    plt.legend([p13,p23,p12], ["13","23","12"])
    plt.axis([-0.1,1.1,-0.1,1.1])

    DrawThreeCategoryPoints(xt[:,0], xt[:,1], yt[:], xlabel="x1", ylabel="x2", show=True, isPredicate=True)

# 主程序
if __name__ == '__main__':
    num_category = 3
    reader = DataReader_1_3(file_name)
    reader.ReadData()
    reader.ToOneHot(num_category, base=1)
    # show raw data before normalization
    ShowData(reader.XRaw, reader.YTrain)
    reader.NormalizeX()

    num_input = 2
    params = HyperParameters_1_1(num_input, num_category, eta=0.1, max_epoch=100, batch_size=10, eps=1e-3, net_type=NetType.MultipleClassifier)
    net = NeuralNet_1_2(params)
    net.train(reader, checkpoint=1)

    xt_raw = np.array([5,1,7,6,5,6,2,7]).reshape(4,2)
    xt = reader.NormalizePredicateData(xt_raw)
    output = net.inference(xt)
    print(output)

    ShowResult(reader.XTrain, reader.YTrain, xt, output)