matlab小波变换学习入门

备注：为了完成课程作业的笔记，内部不连贯，但是足够实用

一：一维小波变换的 matlab 实现

1、dwt 函数：

功能：一维离散小波变换

格式：[cA,cD]=dwt(X, 'wname')——使用指定的小波基函数 ‘wname’ 对信号X进行单层分解，求得的近似系数存放在数组cA中，

细节系数存放在数组cD中

           [cA,cD]=dwt(X,Lo_D,Hi_D)——使用指定的滤波器组 Lo_D、Hi_D 对信号X进行分解

说明：cA 是近似分量；cD 是细节分量；Lo_D 是低通分解滤波器系数；Hi_D 是高通分解滤波器系数

2、idwt 函数：

功能：一维离散小波反变换

格式：X=idwt(cA,cD,'wname')

           X=idwt(cA,cD,'Lo_R,Hi_R')

           X=idwt(cA,cD,'wname',L)

           X=idwt(cA,cD,Lo_R,Hi_R,L)

说明：X=idwt(cA,cD,'wname') 由近似分量 cA 和细节分量 cD 经小波反变换重构原始信号 X，‘wname’ 是所选小波

           X=idwt(cA,cD,'Lo_R,Hi_R') 用指定的重构滤波器 Lo_R 和 Hi_R 经小波反变换重构原始信号 X

           X=idwt(cA,cD,'wname',L) 和 X=idwt(cA,cD,Lo_R,Hi_R,L) 指定返回信号 X 中心附近的 L 个点

3、wavedec 函数：

格式：[C,L]=wavedec(X,N,'wname')

利用小波 'wname' 对信号 X 进行多层分解，返回的近似系数和细节系数都存放在C中，即C=[cA,cD]，L存放是近似和各阶细节系

数对应的长度

A=appcoef(C,L,'wname',N)

4、补充：

dwt2 是二维单尺度小波变换，其可以通过指定小波或者分解滤波器进行二维单尺度小波分解

dwt2 的一种语法格式是 [cA,cH,cV,cD]=dwt2(X,'wname')

wavedec2 是二维多尺度小波分解

wavedec2 的语法格式是 [C,S]=wavedec2(X,N,'wname')，其中 N 为大于1的正整数

也就是说， dwt2 只能对某个输入矩阵 X 进行一层分解，而 wavedec2 可以对输入矩阵 X 进行 N 层分解

二、信号重构：

wrcoef2 函数是用来重建一幅图像的系数，其实就是根据小波分解之后的系数 c 来重建其对应的图像。重建好的图像的尺度与原

始图像一致。即无论你要重构哪个层的系数，最终它的维度都是和原始图像的尺度一致。其调用形式如下：

（1） X = wrcoef2(‘type’,c,s,’wname’,N)

（2） X = wrcoef2(‘type’,c,s,Lo_R,Hi_R,N)

（3） X = wrcoef2(‘type’,c,s,’wname’)

（4） X = wrcoef2(‘type’,c,s,Lo_R,Hi_R)

第一种调用形式的参数说明：

type ：指定要进行重构的小波系数，如 a –近似图像 ; h – 水平高频分量; v – 垂直高频分量; d–对角高频分量；

c: 是小波分解函数 wavedec2 分解的小波系数；

s: 是 wavedec2 分解形成的尺度；

wname ：指定小波基；

N ：指定重构的小波系数所在的层。

而形式（3）则是默认重构最大层的系数，N = size(S,1)-2。

对于形式（2）Lo_R 是重建低通滤波器，Hi_R 是重建高通滤波器，形式（4）的默认层数同上面所述一样。

三、关于对一维离散小波变换的理解：

这部分转自博客：一维离散小波变换过程

1、对于一维离散小波变换的理解：

1）.一维小波变换的输入变量是一个【1×n】的矩阵，你也可以把它理解为信号、函数等等

2）.进行离散小波变换需要预先指定两个滤波器，一个是高通滤波器、另一个是低通滤波器

3）.将输入的一维向量和滤波器的系统函数卷积得到两个卷积的结果

4）.得到的两个结果分别进行系数为2的下采样得到两个分量。从低通滤波器获得的分量称为【近似分量】，从高通滤波器获得的

分量称为【细节分量】

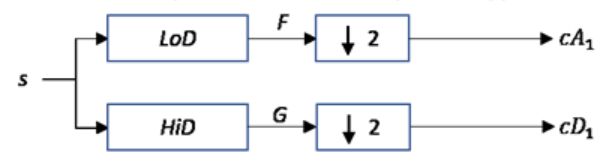
一维离散小波变换的框图可以如下所示：

四、解决作业：

作业描述：基于MATLAB，针对一维信号（可用matlab工具箱自带信号sumsin.mat），实现一维离散小波变换，选用Daubechies小波（如db3）函数，进行五层分解，并对第5层到第1层的低频、高频系数分别进行重构。

1、Daubechies小波：

Daubechies 小波是常用的小波函数之一。小波变换中，通常使用小波系数来选择小波基函数，小波变换后的系数比较大，就表明

小波和信号的波形相似程度较大；反之则比较小。另外根据信号处理的目的来决定尺度的大小，如果小波变换仅仅反映信号整体

的近似程度，往往选用比较大的尺度；反映信号细节的变换则选用尺度不大的小波。

db 小波是小波家族中的一部分，称为 Daubechies 极限相位小波，db 后面的数字表示的是消失矩；一般来说，消失矩的数字越

大，这个小波越光滑，频域的局部化能力就越强，频带的划分效果越好，但是会使时域紧支撑性减弱，同时计算量大大增加，实

时性变差。另外，除 N=1 外，dbN 小波不具有对称性（即非线性相位），即在对信号进行分析和重构时会产生一定的相位失真。

dbN 没有明确的表达式（除了 N=1 外，N=1 时即为 Haar 小波）。

对于 db 小波族的小波函数可以如下图所示：