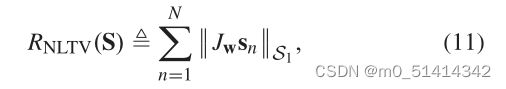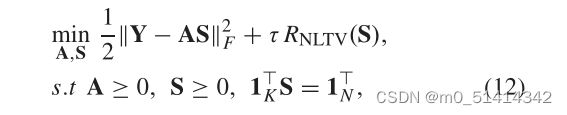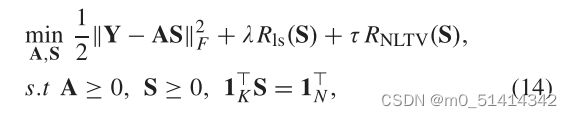Nonconvex-Sparsity and Nonlocal-Smoothness-Based Blind Hyperspectral Unmixing

J. Yao, D. Meng, Q. Zhao, W. Cao and Z. Xu, "Nonconvex-Sparsity and Nonlocal-Smoothness-Based Blind Hyperspectral Unmixing," in IEEE Transactions on Image Processing, vol. 28, no. 6, pp. 2991-3006, June 2019, doi: 10.1109/TIP.2019.2893068.

摘要：

盲高光谱解混(HU)是高光谱数据开发的一项关键技术，其目的是将混合像素分解成由相应的分数丰度加权的组成材料的集合。近年来，基于非负矩阵分解(NMF)的方法越来越受欢迎，并取得了良好的性能。在这些方法中，探讨了两类关于丰度的性质，即稀疏性和结构光滑性，并证明了它们对盲HU的重要性。然而，所有的方法都忽略了自然高光谱图像(HSI)的另一个重要特性，非局部平滑性，即在一个自然高光谱图像(HSI)的更大区域内的相似斑块共享相似的平滑结构。基于之前在其他任务上的尝试，这样的先验结构反映了HSI之下的内在配置，因此有望在很大程度上改善所研究的HU问题的性能。

本文首先考虑HSI中的这种先验，将其编码为非局部总变分(NLTV)正则化子。进一步，通过充分挖掘HSI的内在结构，我们将NLTV推广到非局部HSI TV (NLHTV)，使模型更适合于盲的HU任务。通过将这两种正则化算子与表征丰度映射稀疏性的非凸对数和形式的正则化算子结合到NMF模型中，我们分别提出了新的盲HU模型称为NLTV/NLHTV和对数和正则化NMF (NLTVLSRNMF/NLHTV- lsrnmf)。针对所提出的模型，设计了一种基于可选优化策略(AOS)和乘法器交替方向法(ADMM)的高效算法。在模拟和真实高光谱数据集上进行的大量实验证明了该方法在盲HU任务中优于其他竞争方法。

背景介绍：

通常，盲HU任务可以通过两阶段过程完成。第一阶段对端元数进行估计，这可以使用经典的估计方法，如hysimi[13]和HFC[14]来完成。在第二阶段中，用端元数作为先验估计端元数和相应的丰度。典型的几何方法包括像素纯度指数[16]、N-FINDR[17]、单纯形生长算法[18]和顶点分量分析(VCA)[19]。然而，所有这些方法都假设场景中存在纯像素，因此在缺乏纯像素的情况下效果较差。因此，针对高混合盲HU问题，提出了假设端元在统计上独立或不相关的统计方法，如独立成分分析[20]和非负矩阵分解(NMF)[21]。具体而言，基于nmf的方法经过了实证验证，适用于被调查的HU任务。

传统的NMF对应于一种采用乘法算法[22]将高维矩阵近似分解成两个非负矩阵的乘积的方法。它已成功地应用于许多计算机视觉问题，并显示出很大的潜力。考虑到具体的HU应用，希望在基本的NMF公式中加入额外的约束和先验，以促进问题的可行解决。例如，除了端元和丰度两个基本的非负约束外，丰度和对一约束(ASC)经常被用于缩小解空间。对端元的其他一些约束也可以施加到模型上，包括单纯形体积最小约束[23]，最小色散约束[24]，端元不相似度和平滑性约束[25]。

稀疏性（少量的端元可能对观测光谱有贡献，稀疏性应用到丰度矩阵中）

只有少量的端元可能对观测光谱有贡献，稀疏诱导正则化被发展并集成到盲HU的NMF模型中：

• Bioucas-Dias和Figueiredo[26]首次将L1范数正则子引入HU，作为对L0范数的可解松弛。
• Qian等人[27]提出使用L1/2准范数作为替代，结果表明?1/2准范数比?1范数更能促进稀疏性，且计算效率仍然较高
• Sigurdsson等[29]将Lq(0 < q < 1)-范数正则器，在低信噪比情况下取得了较好的性能。
• 为了进一步增强稀疏性，He等[30]使用了加权1范数正则器，代表了HU问题的最新进展。

分段平滑（对于相同的端元[31]，相邻像素容易有相似的分数丰度。这种分段平滑特征可以用全变分(TV)正则化器有效地表征）

• Iordache等[31]提出了一种基于已知库的TV正则化稀疏回归问题解决非盲HU问题的方法。
• 沿着这条线，He等人[30]提出TV -RSNMF方法来联合推断盲HU的库和丰度。也有其他变体利用相似的相邻像素的规律性
• 例如，Liu等人[32]通过在NMF中引入局部邻域权值，展示了一种鲁棒的HU方法，
• Lu等人的[33]嵌入式图形正则化抓住了高光谱数据的内部流形结构。

上述方法都只考虑了HSI在连续区域内的平滑性，而忽略了自然HSI的另一个内在性质，即非局部平滑性。

为了更好地加强丰度图的稀疏性，我们采用了log-sum惩罚函数，与一般的L1范数相比，它更接近于L0范数。通过将这两种正则化方法引入到NMF模型中，我们提出了一种新的盲HU模型，即NLTV和log-sum正则化NMF (NLTV- lsrnmf)。此外，我们还将NLTV推广到非局域HSI TV (NLHTV)，考虑了HSI不同端元的空间分布差异，得到了NLHTV- lsrnmf模型。

• 通过在丰度上引入NLTV正则化子，我们首次探讨了HSIs的非局部光滑性。因此，我们的方法可以充分利用输入HSI中更大区域的更多空间结构信息，而不仅仅是局部相邻像素，以增强丰度图的重建。

• 通过充分考虑HSIs的内在结构，我们将NLTV推广为NLHTV，以更好地表征不同端元的空间分布差异。

• 为了更好地促进稀疏性，我们建议在模型中使用对数和惩罚函数，与传统的L1范数相比，它更接近L0范数。

NLTV 方法模型：

如前所述，进一步考虑盲HU任务的空间结构信息至关重要，而HSIs的分段平滑性是最常用的结构先验之一。利用HSI数据Y与丰度S之间的线性关系，可以用丰度S的分段平滑度来表示原始HSI的分段平滑度。因此，近年来的研究尝试利用邻近像素信息，在丰度[31]上施加标准TV正则化，或HSI TV (HTV)作为改进的替代[30]。然而，任何一种方法都忽略了丰度梯度信息具有LSR和NSS特性，这些特性可以用非局部光滑性来表征。因此，我们提出采用NLTV正则子来整合局部和非局部光滑先验。具体地说，通过将每个端元的丰度映射看作多通道图像的不同通道，很自然地引入HU的NLTV正则子的定义为：

其中sn∈RK是在像素n处出现的不同端元的比例。将该正则化子嵌入到模型(5)中，可得到如下NLTV正则化NMF:

 盲HU的另一个重要的先验，如导论中所讨论的，是丰度映射的稀疏性。在基本的L1范数的基础上，重加权的L1范数已被证明能够进一步提高稀疏反问题[36]的性能。[36]中指出，重加权L1范数等价于下面的对数和惩罚函数

 

假设重新加权的步骤数趋于无穷，然而，用重加权的1范数精确逼近log-sum惩罚需要大量的重加权步骤，两者都是低效率和无效的。因此，我们直接采用log-sum惩罚，利用[37]中导出的解析解求解。将这个正则化子加入到模型(12)中，我们得到了NLTV-LSRNMF模型:

NLHTV 方法模型：

上一节我们介绍的NLTV是建立在多通道图像的梯度信息上的，因此包含了不同通道之间的强相关性。然而，在HSI场景中，特别是在盲HU任务中，这样的相关性可能是不必要的，甚至会使整体性能退化。从图1可以看出，对于同一组相似的斑块，不同材料的丰度图上的平滑结构是不同的。为了更好地描述上述特性，我们提出以下“逐通道”非局部HSI TV (NLHTV)正则化器

将模型(14)中的NLTV项替换为Eq.(15)，得到NLHTV-LSRNMF模型: