深度学习【2】感知器
目录
- 一.单层感知器
-
- 1.定义
- 2.实例计算
- 3.学习规则(即权值训练方法)
-
- (1).权值调整公式求解
- (2).学习规则计算举例
- (3).Python实现单层感知器权值调整
- 4.单层感知器分类案例
-
- (1).对数据进行分类
- (2).单层感知器处理异或问题(非线性问题)
- 二.多层感知器(BP神经网络)
一.单层感知器
1.定义
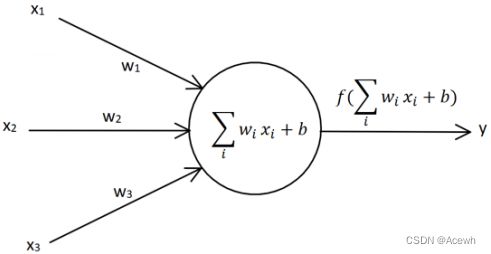
受到生物神经网络的启发,计算机科学家 Frank Rosenblat 在20世纪60年代提出了一种模拟生物网络的人工神经网络结构,称为感知器(Perceptron)。下图为最简单的单层感知器示意图:
- x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3 为输入信号,类似于生物神经网络中的树突;
- w 1 , w 2 , w 3 w_1,w_2,w_3 w1,w2,w3 为输入信号对应的权值,它可以调节信号的大小;
- b b b 为感知器自带的偏置值(Bias);
- ∑ i ( w i x i ) + b \sum_{i}(w_ix_i)+b ∑i(wixi)+b 表示输入信号在感知器内的汇总, ∑ i ( w i x i ) + b = w 1 x 1 + w 2 x 2 + w 3 x 3 + b \sum_{i}(w_ix_i)+b=w_1x_1+w_2x_2+w_3x_3+b ∑i(wixi)+b=w1x1+w2x2+w3x3+b ;
- f ( x ) f(x) f(x) 称为激活函数,可理解为输入信号经过感知器时进行的非线性变化。
将偏置 b b b 改变形式 b = w 0 x 0 b=w_0x_0 b=w0x0,其中 x 0 = 1 x_0=1 x0=1 ,感知器的示意图可表示为:
此时 ∑ i ( w i x i ) + b = ∑ i ( w i x i ) = w 0 x 0 + w 1 x 1 + w 2 x 2 + w 3 x 3 \sum_{i}(w_ix_i)+b=\sum_{i}(w_ix_i)=w_0x_0+w_1x_1+w_2x_2+w_3x_3 ∑i(wixi)+b=∑i(wixi)=w0x0+w1x1+w2x2+w3x3 。
2.实例计算
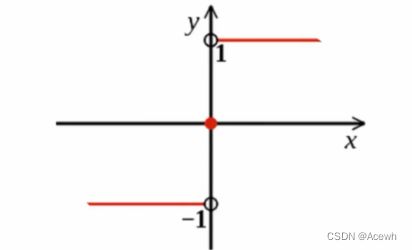
单层感知器中一般使用 s i g n ( x ) sign(x) sign(x) 为激活函数,该函数的特点是当 x > 0 时 y = 1 x>0 时 y=1 x>0时y=1,当 x = 0 时 y = 0 x=0 时 y=0 x=0时y=0,当 x < 0 时 y = − 1 x<0 时 y=-1 x<0时y=−1。
现给定如下初始值,它们的输出分别为:
| x 1 x1 x1 | x 2 x2 x2 | x 3 x3 x3 | w 1 w1 w1 | w 2 w2 w2 | w 3 w3 w3 | w 0 ( 即偏置 ) w_0(即偏置) w0(即偏置) | ∑ i ( w i x i ) \sum_i(w_ix_i) ∑i(wixi) | y ( 即 s i g n ( ∑ i ( w i x i ) ) ) y(即sign(\sum_i(w_ix_i))) y(即sign(∑i(wixi))) |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0.1 | 0.2 | 0.3 | -0.5 | -0.5 | -1 |
| 0 | 0 | 1 | 0.1 | 0.2 | 0.3 | -0.5 | -0.2 | -1 |
| 0 | 1 | 0 | 0.1 | 0.2 | 0.3 | -0.5 | -0.3 | -1 |
| 0 | 1 | 1 | 0.1 | 0.2 | 0.3 | -0.5 | 0 | 0 |
| 1 | 0 | 0 | 0.1 | 0.2 | 0.3 | -0.5 | -0.4 | -1 |
| 1 | 0 | 1 | 0.1 | 0.2 | 0.3 | -0.5 | -0.1 | -1 |
| 1 | 1 | 0 | 0.1 | 0.2 | 0.3 | -0.5 | -0.2 | -1 |
| 1 | 1 | 1 | 0.1 | 0.2 | 0.3 | -0.5 | 0.1 | 1 |
3.学习规则(即权值训练方法)
我们根据训练公式来对单层感知器表达式中的权值进行训练,当训练完毕后,该感知器算法便可进行使用,这也是人工智能算法训练的基本点。
(1).权值调整公式求解
-
单层感知器表达式: y = f ( ∑ i = 0 n w i x i ) i = 0 , 1 , 2... , f 是 s i g n 激活函数 y=f(\sum_{i=0}^{n}w_ix_i) \quad i =0,1,2...,f是sign激活函数 y=f(∑i=0nwixi)i=0,1,2...,f是sign激活函数
-
第 i i i 个权值的调整规则: Δ w i = η ( t − y ) x i η 为学习率 , t 为真实标签 \Delta w_i = \eta (t-y)x_i \quad \eta为学习率,t为真实标签 Δwi=η(t−y)xiη为学习率,t为真实标签
-
权值调整公式为: w i = w i + Δ w i w_i=w_i + \Delta w_i wi=wi+Δwi
(学习规则在《反向传播神经网络》中详解)
由于此处使用的是 s i g n sign sign 激活函数,所以 t 和 y t和y t和y 都是在 [ − 1 , 0 , 1 ] [-1,0,1] [−1,0,1] 中取值,导致 t − y t-y t−y 的值只有 [ − 2 , 0 , 2 ] [-2,0,2] [−2,0,2] 这三种值,可以推出 Δ w i = ± 2 η x i \Delta w_i=\pm2\eta x_i Δwi=±2ηxi 。
(2).学习规则计算举例
假设给定 x 0 = 1 , x 1 = 0 , x 2 = − 1 , w 0 = − 5 , w 1 = 0 , w 2 = 0 , η = 1 , t = 1 x_0=1,x_1=0,x_2=-1,w_0=-5,w_1=0,w_2=0,\eta=1,t=1 x0=1,x1=0,x2=−1,w0=−5,w1=0,w2=0,η=1,t=1,权值调整步骤如下:
-
Step1:
-
y = s i g n ( − 5 ∗ 1 + 0 ∗ 0 + − 1 ∗ 0 ) = s i g n ( − 5 ) = − 1 y=sign(-5*1+0*0+-1*0)=sign(-5)=-1 y=sign(−5∗1+0∗0+−1∗0)=sign(−5)=−1
-
Δ w 0 = η ( t − y ) x 0 = 1 ∗ ( 1 + 1 ) ∗ 1 = 2 \Delta w_0=\eta(t-y)x_0=1*(1+1)*1=2 Δw0=η(t−y)x0=1∗(1+1)∗1=2
Δ w 1 = η ( t − y ) x 1 = 1 ∗ ( 1 + 1 ) ∗ 0 = 0 \Delta w_1=\eta(t-y)x_1=1*(1+1)*0=0 Δw1=η(t−y)x1=1∗(1+1)∗0=0
Δ w 2 = η ( t − y ) x 2 = 1 ∗ ( 1 + 1 ) ∗ ( − 1 ) = − 2 \Delta w_2=\eta(t-y)x_2=1*(1+1)*(-1)=-2 Δw2=η(t−y)x2=1∗(1+1)∗(−1)=−2
-
w 0 = w 0 + Δ W 0 = − 5 + 2 = − 3 w_0=w_0+\Delta W_0=-5+2=-3 w0=w0+ΔW0=−5+2=−3
w 1 = w 1 + Δ W 1 = 0 + 0 = 0 w_1=w_1+\Delta W_1=0+0=0 w1=w1+ΔW1=0+0=0
w 2 = w 2 + Δ W 2 = 0 − 2 = − 2 w_2=w_2+\Delta W_2=0-2=-2 w2=w2+ΔW2=0−2=−2
-
-
Step2:
-
y = s i g n ( − 3 ∗ 1 + 0 ∗ 0 − 2 ∗ ( − 1 ) ) = s i g n ( − 1 ) = − 1 y=sign(-3*1+0*0-2*(-1))=sign(-1)=-1 y=sign(−3∗1+0∗0−2∗(−1))=sign(−1)=−1
-
Δ w 0 = η ( t − y ) x 0 = 1 ∗ ( 1 + 1 ) ∗ 1 = 2 \Delta w_0=\eta(t-y)x_0=1*(1+1)*1=2 Δw0=η(t−y)x0=1∗(1+1)∗1=2
Δ w 1 = η ( t − y ) x 1 = 1 ∗ ( 1 + 1 ) ∗ 0 = 0 \Delta w_1=\eta(t-y)x_1=1*(1+1)*0=0 Δw1=η(t−y)x1=1∗(1+1)∗0=0
Δ w 2 = η ( t − y ) x 2 = 1 ∗ ( 1 + 1 ) ∗ ( − 1 ) = − 2 \Delta w_2=\eta(t-y)x_2=1*(1+1)*(-1)=-2 Δw2=η(t−y)x2=1∗(1+1)∗(−1)=−2
-
w 0 = w 0 + Δ W 0 = − 3 + 2 = − 1 w_0=w_0+\Delta W_0=-3+2=-1 w0=w0+ΔW0=−3+2=−1
w 1 = w 1 + Δ W 1 = 0 + 0 = 0 w_1=w_1+\Delta W_1=0+0=0 w1=w1+ΔW1=0+0=0
w 2 = w 2 + Δ W 2 = − 2 − 2 = − 4 w_2=w_2+\Delta W_2=-2-2=-4 w2=w2+ΔW2=−2−2=−4
-
-
Step3:
- y = s i g n ( − 1 ∗ 1 + 0 ∗ 0 − 4 ∗ ( − 1 ) ) = s i g n ( 3 ) = 1 y=sign(-1*1+0*0-4*(-1))=sign(3)=1 y=sign(−1∗1+0∗0−4∗(−1))=sign(3)=1
此时 y = t = 1 y=t=1 y=t=1 ,感知器的训练结果正确,便可以结束训练了。
(3).Python实现单层感知器权值调整
import numpy as np
# 初始化参数设置
x0, x1, x2 = 1, 0, -1
w0, w1, w2 = -5, 0, 0
lr = 1
t = 1
for i in range(1, 50):
print('第{0}次训练前---w0={1},w1={2},w2={3}'.format(i, w0, w1, w2))
y = np.sign(w0 * x0 + w1 * x1 + w2 * x2)
if (y != t):
print('第{0}次进行训练'.format(i))
w0 = w0 + lr * (t - y) * x0
w1 = w1 + lr * (t - y) * x1
w2 = w2 + lr * (t - y) * x2
else:
print('最终的权值结果为w0={1},w1={2},w2={3}'.format(i, w0, w1, w2))
break
'''
第1次训练前---w0=-5,w1=0,w2=0
第1次进行训练
第2次训练前---w0=-3,w1=0,w2=-2
第2次进行训练
第3次训练前---w0=-1,w1=0,w2=-4
最终的权值结果为w0=-1,w1=0,w2=-4
可以看到和我们手动推导的结果一致
'''
4.单层感知器分类案例
(1).对数据进行分类
题目:
以二元一次方程为例,假设二维平面上有四个点:(3,3),(4,3),(1,1),(2,1),它们对应的真实分类结果 T 为 [ 1 , 1 , − 1 , − 1 ] T为[1,1,-1,-1] T为[1,1,−1,−1]。
将偏置值设为节点, x 0 x_0 x0 统一为1,上述的四个点可以扩展为下列点:
(1,3,3),(1,4,3),(1,1,1),(1,2,1) —> (1,1,-1,-1)
要求对它们进行分类。
import numpy as np
import matplotlib.pyplot as plt
def train():
global X, Y, W, lr
Y = np.sign(np.dot(X, W)) # 将X与权值W相乘求和再进行激活函数变换得到预测值 Y,四个样本得出4个Y,4行1列
E = T - Y # 4个样本真实值与预测值的误差E
delta_W = lr * (X.T.dot(E)) / int(X.shape[0]) # 样本数 X.shape[0]
W = W + delta_W
if __name__ == '__main__':
X = np.array([[1, 3, 3],
[1, 4, 3],
[1, 1, 1],
[1, 2, 1]])
T = np.array([[1],
[1],
[-1],
[-1]])
W = np.random.random((3, 1))
lr = 0.11
Y = 0
for i in range(100):
train()
print("当前权值", W)
print("当前迭代次数", i + 1)
Y = np.sign(np.dot(X, W)) # 当前预测值
print("当前预测值")
print(Y)
if (T == Y).all():
print("总共迭代次数:", i + 1)
print("程序结束")
break
print("===================")
x1 = [3, 4]
y1 = [3, 3]
x2 = [1, 2]
y2 = [1, 1]
k = -W[1] / W[2]
b = -W[0] / W[2]
print("k=:", k)
print("b=:", b)
xdata = (0, 5)
ydata = xdata * k + b
plt.plot(xdata, ydata, 'g')
plt.scatter(x1, y1, c='b')
plt.scatter(x2, y2, c='r')
plt.show()
注意:
神经网络的信号总和为 w 0 ∗ x 0 + w 1 ∗ x 1 + w 2 ∗ x 2 w0*x0 + w1*x1 + w2*x2 w0∗x0+w1∗x1+w2∗x2,
当信号总和大于0再经过激活函数,模型的预测值会得到1,
当信号总和小于0再经过激活函数,模型的预测值会得到-1,
当信号总和时为0时为分类边界,
所以在画图时把 x1和x2分别看成是坐标系中的x轴和y轴
可以得到 w0 + w1x + w2y = 0 为分界线 (x0 = 1)
y = − W [ 1 ] x / W [ 2 ] − W [ 0 ] / W [ 2 ] y = -W[1]x/W[2] - W[0]/W[2] y=−W[1]x/W[2]−W[0]/W[2]
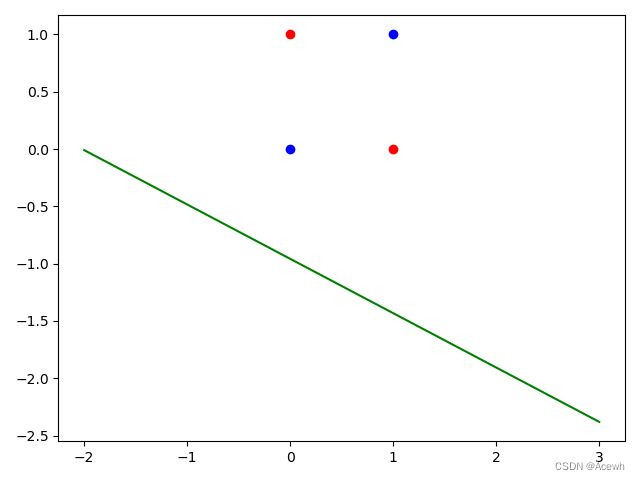
(2).单层感知器处理异或问题(非线性问题)
'''
异或非线性问题
0^0 = 0
0^1 = 1
1^0 = 1
1^1 = 0
'''
import numpy as np
import matplotlib.pyplot as plt
def train():
global X,Y,W,lr
Out = np.sign(np.dot(X,W))
W_C = lr*(X.T.dot(Y-Out)) / int(X.shape[0])
W = W + W_C
if __name__ == '__main__':
X = np.array([[1, 0, 0],
[1, 0, 1],
[1, 1, 0],
[1, 1, 1]])
Y = np.array([[-1],
[1],
[1],
[-1]])
W = (np.random.random((3, 1)) - 0.5) * 2
lr = 0.11
Out = 0
for i in range(100):
train()
if (Out == Y).all():
print("总共迭代次数:", i + 1)
print("程序结束")
break
x1 = [0,1]
y1 = [0,1]
x2 = [1,0]
y2 = [0,1]
k = -W[1]/W[2]
b = -W[0]/W[2]
print("k=:",k)
print("b=:",b)
xdata = (-2,3)
ydata = xdata*k + b
print(ydata)
plt.plot(xdata,ydata,'g')
plt.scatter(x1,y1,c='b')
plt.scatter(x2,y2,c='r')
plt.show()
注意:无论迭代多少次都不能正确分类
二.多层感知器(BP神经网络)
简单的感知器只能求解线性问题,不能处理非线性问题,必须引入多个神经元层,即多个隐藏层才能更好的解决非线性问题。多层感知器的特点就是有多个神经元层,结合反向传播算法,又称为BP神经网络。
其余内容详见下节。