LSTM及其变种及其克服梯度消失

本宝宝又转了一篇博文，但是真的很好懂啊：

写在前面：知乎上关于lstm能够解决梯度消失的问题的原因：

 

上面说到，LSTM 是为了解决 RNN 的 Gradient Vanish 的问题所提出的。关于 RNN 为什么会出现 Gradient Vanish，上面已经介绍的比较清楚了，本质原因就是因为矩阵高次幂导致的。下面简要解释一下为什么 LSTM 能有效避免 Gradient Vanish。

对于 LSTM，有如下公式

模仿 RNN，我们来计算 ，有

<img src="https://pic4.zhimg.com/v2-8eb676e7c1bac3eb131d8e0bf2f7db5b_b.png" data-rawwidth="147" data-rawheight="149" class="content_image" width="147">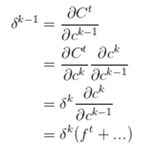

公式里其余的项不重要，这里就用省略号代替了。可以看出当 时，就算其余项很小，梯度仍然可以很好导到上一个时刻，此时即使层数较深也不会发生 Gradient Vanish 的问题；当 时，即上一时刻的信号不影响到当前时刻，则梯度也不会回传回去； 在这里也控制着梯度传导的衰减程度，与它 Forget Gate 的功能一致。

 

传统RNN，BPTT(BACK propagation through time）梯度回传时候会有连成，tanh【0，1】 sigmoid(0,1/4),导致梯度消失，虽然可以替换激活函数，RELU，但是LSTM可以解决呀

　　通常，数据的存在形式有语音、文本、图像、视频等。因为我的研究方向主要是图像识别，所以很少用有“记忆性”的深度网络。怀着对循环神经网络的兴趣，在看懂了有关它的理论后，我又看了Github上提供的tensorflow实现，觉得收获很大，故在这里把我的理解记录下来，也希望对大家能有所帮助。本文将主要介绍RNN相关的理论，并引出LSTM网络结构（关于对tensorflow实现细节的理解，有时间的话，在下一篇博文中做介绍）。

循环神经网络

　　RNN，也称作循环神经网络（还有一种深度网络，称作递归神经网络，读者要区别对待）。因为这种网络有“记忆性”，所以主要是应用在自然语言处理（NLP）和语音领域。与传统的Neural network不同，RNN能利用上”序列信息”。从理论上讲，它可以利用任意长序列的信息，但由于该网络结构存在“消失梯度”问题，所以在实际应用中，它只能回溯利用与它接近的time steps上的信息。

1. 网络结构

　　常见的神经网络结构有卷积网络、循环网络和递归网络，栈式自编码器和玻尔兹曼机也可以看做是特殊的卷积网络，区别是它们的损失函数定义成均方误差函数。递归网络类似于数据结构中的树形结构，且其每层之间会有共享参数。而最为常用的循环神经网络，它的每层的结构相同，且每层之间参数完全共享。RNN的缩略图和展开图如下，

 

 

　　尽管RNN的网络结构看上去与常见的前馈网络不同，但是它的展开图中信息流向也是确定的，没有环流，所以也属于forward network，故也可以使用反向传播（back propagation）算法来求解参数的梯度。另外，在RNN网络中，可以有单输入、多输入、单输出、多输出，视具体任务而定。

2. 损失函数

　　在输出层为二分类或者softmax多分类的深度网络中，代价函数通常选择交叉熵（cross entropy）损失函数，前面的博文中证明过，在分类问题中，交叉熵函数的本质就是似然损失函数。尽管RNN的网络结构与分类网络不同，但是损失函数也是有相似之处的。 
　　假设我们采用RNN网络构建“语言模型”，“语言模型”其实就是看“一句话说出来是不是顺口”，可以应用在机器翻译、语音识别领域，从若干候选结果中挑一个更加靠谱的结果。通常每个sentence长度不一样，每一个word作为一个训练样例，一个sentence作为一个Minibatch，记sentence的长度为T。为了更好地理解语言模型中损失函数的定义形式，这里做一些推导，根据全概率公式，则一句话是“自然化的语句”的概率为

p(w1,w2,...,wT)=p(w1)×p(w2|w1)×...×p(wT|w1,w2,...,wT−1)

　　所以语言模型的目标就是最大化 P(w1,w2,...,wT)。而损失函数通常为最小化问题，所以可以定义

Loss(w1,w2,...,wT|θ)=−logP(w1,w2,...,wT|θ)

　　那么公式展开可得

Loss(w1,w2,...,wT|θ)=−(logp(w1)+logp(w2|w1)+...+logp(wT|w1,w2,...,wT−1))

　　展开式中的每一项为一个softmax分类模型，类别数为所采用的词库大小（vocabulary size)，相信大家此刻应该就明白了，为什么使用RNN网络解决语言模型时，输入序列和输出序列错了一个位置了。

 

3. 梯度求解

　　在训练任何深度网络模型时，求解损失函数关于模型参数的梯度，应该算是最为核心的一步了。在RNN模型训练时，采用的是BPTT（back propagation through time）算法，这个算法其实实质上就是朴素的BP算法，也是采用的“链式法则”求解参数梯度，唯一的不同在于每一个time step上参数共享。从数学的角度来讲，BP算法就是一个单变量求导过程，而BPTT算法就是一个复合函数求导过程。接下来以损失函数展开式中的第3项为例，推导其关于网络参数U、W、V的梯度表达式（总损失的梯度则是各项相加的过程而已）。 
　　为了简化符号表示，记E3=−logp(w3|w1,w2)，则根据RNN的展开图可得，

 

s3=tanh(U×x3+W×s2)；　　s2=tanh(U×x2+W×s1)s1=tanh(U×x1+W×s0)；　　s0=tanh(U×x0+W×s−1)(1)

 

　　所以，

 

∂s3W=∂s3W1+∂s3∂s2×∂s2W∂s2W=∂s2W1+∂s2∂s1×∂s1W∂s1W=∂s1W0+∂s1∂s0×∂s0W∂s0W=∂s0W1(2)

 

　　说明一下，为了更好地体现复合函数求导的思想，公式（2）中引入了变量W1，可以把W1看作关于W的函数，即W1=W。另外，因为s−1表示RNN网络的初始状态，为一个常数向量，所以公式（2）中第4个表达式展开后只有一项。所以由公式（2）可得，

 

∂s3W=∂s3W1+∂s3∂s2×∂s2W1+∂s3∂s2×∂s2∂s1×∂s1W1+∂s3∂s2×∂s2∂s1×∂s1∂s0×∂s0W1(3)

 

　　简化得下式，

 

∂s3W=∂s3W1+∂s3∂s2×∂s2W1+∂s3∂S1×∂s1W1+∂s3∂s0×∂s0W1(4)

 

　　继续简化得下式，

 

∂s3W=∑i=03∂s3∂si×∂siW1(5)

 

3.1 E3关于参数V的偏导数

　　记t=3时刻的softmax神经元的输入为a3，输出为y3，网络的真实标签为y(1)3。根据函数求导的“链式法则”，所以有下式成立，

 

∂E3V=∂E3∂a3×∂a3∂V=(y(1)3−y3)⨂s3(6)

 

3.2 E3关于参数W的偏导数

　　关于参数W的偏导数，就要使用到上面关于复合函数的推导过程了，记zi为t=i时刻隐藏层神经元的输入，则具体的表达式简化过程如下，

 

∂E3W=∂E3∂s3×∂s3∂W=∂E3∂a3×∂a3∂s3×∂s3∂W=∑k=03∂E3∂a3×∂a3∂s3×∂s3∂sk×∂sk∂W1=∑k=03∂E3∂a3×∂a3∂s3×∂s3∂sk×∂sk∂zk×∂

转载于:https://www.cnblogs.com/wuxiangli/p/7096392.html