基于骨架动作识别的时空图卷积网络

论文来自https://arxiv.org/abs/1801.07455
英语渣渣的阅读和翻译

---

基于骨架动作识别的时空图卷积网络

• 摘要：人体骨骼动力学为人类动作识别传达了重要信息。传统方法在骨骼建模上通常依赖于手工制作的部分或遍历的规则，因此就导致了传统方法的表达力有限和泛化困难。在这项工作中，我们提出了一种动态骨架的新模型，称为时空图卷积网络（ST-GCN），它通过自动从数据中学习时空模式，超越了以前方法的局限。这种表述不仅导致更大的表达能力，而且还具有更强的泛化能力。在两个大型数据集Kinetics和NTU-RGBD上，与主流方法相比，它取得了实质性的改进。

1 引言

• 近年来，人类动作识别已经成为活跃的研究领域，因为它在视频理解中起着重要作用。一般而言，人类行为可以从多种形式（Simonyan和Zisserman 2014；Tran等人2015；Wang，Qiao和Tang 2015；Wang等人2016；Zhao等人2017）中识别，例如外观、深度、光学流和人体骨骼（Du，Wang和Wang 2015；Liu等人2016）。在这些方式中，动态的人体骨骼通常传达重要的信息，这些信息是其他信息的补充。但是，与外观和光学流相比，动态骨骼的模型受到的关注相对较少。在这项工作中，我们系统的地研究了这种模式，目的是开发一种有效的方法来对动态骨骼建模并利用它们进行动作识别。
• 动态骨骼模型可以由人类关节位置的时间序列以2D或3D坐标的形式自然地表示。然后可以通过分析其动作模式来识别人的动作。早期使用骨骼进行动作识别的的方法只是在各个时间步上采用关节坐标来形成特征向量，然后对其进行时间分析（Wang等人2012；Fernando等人2015）。这些方法的能力有限，因为它没有明确利用这些关节之间的空间关系，而这些关系对于理解人类行为是十分关键的。最近，已开发出尝试利用关节之间自然连接的新方法（Shahroudy等人2016；Du，Wang和Wang 2015）。这些方法显示出令人鼓舞的改进，这表明了连接的重要性。但是，大多数现有方法都依赖于手工制作的部分或规则来分析空间的模式。结果，为特定应用而设计的模型很难推广到其他模型。
• 为了克服这些限制，我们需要一种新的方法，该方法可以自动捕获嵌入在关节空间配置中的模式及其时间动态。这就是深度神经网络的优势。但是如前所述，骨骼是图形形式，而不是2D或3D网络，这就导致很难使用卷积网络之类的成熟模型。最近，将卷积神经网络（CNNs）概括为任意结构图的图神经网络（GCNs）得到了越来越多的关注，并且成功在许多应用中被采用，例如图像分类（Bruna等人2014），文档分类（Defferrard，Bresson和Vandergheynst 2016）和半监督学习（Kipf和Welling 2017）。然而，许多这样的先前工作都是以固定图形作为输入。而GCNs在大型数据集（例如人类骨骼序列）的模型动态图上的应用还有待探索。

图1.本文提出的ST-GCN会在此工作中使用的骨骼序列的时空图。蓝点表示身体的关节。人体关节之间的体内的边是根据人体的自然连接定义的。框架间的边表示连续框架之间的相同关节。关节坐标被用作ST-GCN的输入。

• 在本文中，我们提出通过将图神经网络扩展到称为时空图卷积网络（ST-GCN）的时空图模型，来设计用于行为识别的骨骼序列的通用表示。如图1所示，此模型是在一系列骨骼图的初始建立的，其中每个节点对应于人体的一个关节。边有两种类型，即与关节的自然连接性相符的空间边和在连续的时间上连接相同关节的时间边。在其上构建了多层的空间时间图卷积，这使信息可以沿着图和时间维度集成。
• ST-GCN的分层特性消除了手工制作部分或遍历规则的需要。这不仅可以提高表达能力，从而提高性能（如我们实验所示），而且还可以很容易地将其推广到不同的环境，在通用GCN公式的基础上，我们还从图像模型的灵感中研究了设计图卷积核的新策略。
• 这项工作的主要贡献在于三个方面：
  1. 我们提出ST-GCN，这是一种基于图的通用模型，用于对动态骨架进行建模，这是第一个为此应用基于图的神经网络的方法。
  2. 我们提出了一些在ST-GCN中设计卷积核的原则，以满足骨架建模的特定要求。
  3. 在两个基于骨架的动作识别的大型数据集上，与以前使用手工制部分或遍历规则的方法相比，所提出的模型具有更高的性能，而在人工设计上的工作量却大大减少。

2 相关工作

• 图上的神经网络。将神经网络泛化为具有图结构的数据是深度学习研究中的一个新兴主题。讨论的神经网络架构既包括递归神经网络（Tai，Socher和Manning 2015；Van Oord，Kalchbrenner和Kavukcuoglu 2016）和卷积神经网络（CNNs）（Bruna等人 2014；Henaff，Bruna和LeCun 2015；Li等人 2016；Defferrard，Bresson和Vandergheynst 2016）。这项与CNNs或图卷积网络（GCNs）的泛化有关。在图上构造GCN的原理通常遵循两个流：

  1. 光谱透视图，其中以光谱分析的形式考虑了图卷积的局部性（Henaff，Bruna和LeCun 2015；Duvenaud等人 2015；Li等人 2016；Kipf和Welling 2017）。
  2. 空间透视图，将卷积过滤器直接用于图节点及其邻居（Bruna等人 2014；Niepert，Ahmed和Kutzkov 2016）。

  这项工作延续了第二个流的精神，通过将每个过滤器的应用限制到每个节点的1个邻居，我们在空间域上构造CNN过滤器。

• 基于骨架的动作识别。人体的骨骼和关节轨迹对于光照变化和场景变化具有鲁棒性，并且由于高度精确的深度传感器或姿势估计算法而易于获得（Shotton等人 2011；Cao等人 2017），因此，存在多种基于骨架的动作识别方法。这些方法可以分为基于手工特征的方法和深度学习方法。第一种方法设计了一些手工制作的特征来捕获关节运动。这些可能是关节轨迹的协方差矩阵（Hussein等人 2013），关节的相对位置（Wang等人 2012）或身体各部位之间的旋转和平移（Vemupalalli，Arrate和Chellappa 2014）。最近深度学习的成功导致了基于深度学习的骨架建模方法的激增。这些工作一直使用递归神经网络（Shahroudy等人 2016；Zhu等人 2016；Liu等人 2016；Zhang，Liu和Xiao 2017）和时间CNNs（Li等人 2017；Ke等人 2017；Kim和Reiter 2017）以端到端的方式学习动作识别模型。在这些方法中，许多人都强调了对人体各部位关节建模的重要性。但是通常使用领域知识明确分配这些部分。我们的ST-GCN是第一个将图CNNs用于骨骼的动作识别。它与以前的方法的不同之处在于，它可以通过利用图卷积的局部性和时间动态来隐式地学习部分信息。通过消除手动部分分配的需求，该模型更易于设计，并且可以有效地学习更好的动作表示。

图2.我们对视频执行姿势估计，并在骨架序列上构建空间时间图。将应用多层时空图卷积（ST-GCN），并逐步在图上生成更高级别的特征图。然后，将由标准Softmax分类器将其分类为相应的动作类别。

3 时空图卷积网

• 在进行活动时，人体关节会在小范围进行运动，这被称为“身体部位”。现有的基于骨骼的动作识别方法已经验证了在建模中引入身体部位的有效性（Shahroudy等人 2016；Liu等人 2016；Zhang，Liu和Xiao 2017）。我们认为，这种改进主要是由于与整个骨架相比，部位限制了“局部区域”内关节轨迹的建模，从而形成了骨架序列的层次表示。在诸如图像对象识别之类的任务中，通常通过卷积神经网络的固有属性（Krizhevsky，Sutskever和Hinton 2012）来实现层次表示和局部性，而不是手动分配对象部分。它促使我们将CNNs的这种特点引入到基于骨架的动作识别中。这样做的结果就是产生了ST-GCN模型。

3.1 流程概述

• 基于骨架的数据可以从运动捕获设备获得，也可以从视频中获取姿势估计算法。通常来说，数据是一系列的帧，每一帧将具有一组联合坐标。给定2D或3D坐标形式的身体关节序列，我们以关节为图节点，以人体结构中的自然连接性和时间为图边，构造一个时空图。因此ST-GCN的输入是图形节点上的关节坐标矢量。可以将其视为基于图像的CNNs的模拟，其中输入是由2D图像网络上的像素强度矢量形成的。多层时空图卷积操作将应用于输入数据，并在图上生成更高级别的特征图。然后，它将由标准的Softmax分类器分类为相应的动作类别。整个模型通过反向传播以端到端的方式进行训练。现在，我们将介绍ST-GCN模型中的组件。

3.2 骨架图构造

• 骨骼序列通常由每个帧中每个人体关节的2D或3D坐标表示，以前使用卷积进行骨骼动作识别的工作（Kim和Reiter 2017）将所有关节的坐标向量连接起来，从而每帧形成一个特征向量。在我们的工作中，我们将时空图用于骨架序列的分层表示。特别是，我们具有N个关节和T帧（同时具有体内和帧间连接）的骨架序列上构造了无方向的时空图$G=(V,E)$。
• 在这个图中，节点集$V=\{v_{ti}|t=1,...,T,i=1,...,N\}$包括骨骼序列中的所有关节。作为ST-GCN的输入，节点$F(v_{ti})$上的特征矢量包括帧t上第i个关节的坐标矢量以及估计置信度。我们分两步在骨架序列上构建时空图。首先，根据人体结构的连通性，将一帧内的关节用边连接起来，就像图1中展示的那样。然后，每个关节将在连续框架中连接到同一关节。因此，无需手动分配部分即可自然自然定义此设置中的连接。这也使网络体系结构可以处理具有不同数量的关节或关节连通性的数据集。例如，在Kinetics数据集上，我们使用来自OpenPose（Cao等人 2017）工具箱的2D姿态估计结果，该结果输出18个关节，而在NTU-RGB+D数据集（Shahroudy等人 2016）中我们使用3D关节跟踪结果作为输入，产生25个关节。可以在两种情况下定义ST-GCN，并提供一致的卓越性能。图1展示了一个构造的空间时间图的例子。
• 形式上，边集E由两个子集组成，第一个子集描述每帧的骨架内连接，表示为$E_S=\{v_{ti}{v}_{tj}|(i,j)\in H\}$，其中H是自然连接的人的集合身体关节点。第二个子集包含帧间边，这些边将连续帧中的相同关节连接为$E_F=\{v_{ti}{v}_{(t+1)i}\}$。因此，一个特定关节的$E_F$的所有边i都会随着时间的推移而显现其轨迹。

3.3 空间图卷积神经网络

• 在深入研究成熟的ST-GCN之前，我们首先要在一个帧内查看CNN图模型。在这种情况下，在时间$\tau$的单个帧上，将有N个关节节点$V_t$以及骨架边$E_S(\tau )=\{v_{ti}{v}_{tj}|t=\tau ,(i,j)\in H\}$。回想一下在2D自然图像或特征图上的卷积运算的定义，它们都可以视为2D网格。卷积运算的输出特征图还是2D网格，使用步长为1和适当的填充，输出的特征图可以具有与输入特征图相同的大小。在下面的讨论中，我们将假定这种情况。给定内核大小为$K\times K$的卷积运算，并且输入特征图$f_{in}$的通道数为c，那么在空间位置x上的单个通道的输出值可以写成
  $$f_{out}(\mathbf{x})=\sum _{h=1}^K\sum _{w=1}^K{f}_{in}(\mathbf{p}(\mathbf{x},h,w))\cdot \mathbf{w}(h,w)\text{\hspace{1em}(1)}$$
• 其中采样函数$\mathbf{p}:Z^2\times Z^2\to Z^2$枚举$\mathbf{x}$的邻居。在图像卷积的情况下，也可以表示为$\mathbf{p}(\mathbf{x},h,w)=\mathbf{x}+{\mathbf{p}}^{\prime }(h,w)$。权重函数$\mathbf{w}:Z^2\to {\mathbb{R}}^c$在c维实数空间中提供权重矢量。用于使用采样的尺寸为c的输入特征向量计算内部产品。。请注意，权重函数与输入位置$\mathbf{x}$不相关。因此，滤波器权重在输入图像上的所有位置共享。所以，通过在$\mathbf{p}(\mathbf{x})$中编码矩形网格，可以实现图像域上的标准卷积。可以在（Dai等人 2017）中找到有关此公式的更多详细说明和其他应用程序。
• 然后，通过上述公式扩展到输入特征图位于空间图$V_t$上的情况，来定义图上的卷积运算。也就是在特征图$f_{in}^t:V_t\to {\mathbb{R}}^c$上的每一个节点都有一个向量。扩展的下一步是重新定义采样函数$\mathbf{p}$和权重函数$\mathbf{w}$。
• 采样函数，在图像上，中心位置$\mathbf{x}$在相邻像素上定义了采样函数$\mathbf{p}(h,w)$。在图上，我们可以类似地在节点$v_{ti}$的邻居集$B(v_{ti})=\{v_{tj}|d(v_{tj},v_{ti})\le D\}$上来定义采样函数。此处的$d(v_{tj},v_{ti})$表示从$v_{tj}$到$v_{ti}$的所有路径的最小长度。因此，采样函数$\mathbf{p}:B(v_{ti})\to V$可以写成
  $$\mathbf{p}(v_{ti},v_{tj})=v_{tj}\text{\hspace{1em}(2)}$$
  在这项工作，我们使用$D=1$在所有的情况中，也就是关节节点的1个邻居集。至于$D$的数量为更多的情况就留给以后的工作。
• 权重函数，与采样函数相比，权重函数很难定义。在2D卷积中，中心位置周围自然会存在一个固定的网格。因此，邻居内的像素可以具有固定的空间顺序。然后可以通过根据空间顺序索引$(c,K,K)$维的张量来实现权重函数。对于像我们刚刚构建的一般图形，没有这样的隐式排列。该问题的解决方案首先在（Niepert，Ahmed和Kutzkov 2016）中进行了研究，其中顺序是通过根节点周围的邻居图中的图标记过程定义的。我们遵循这个想法来构造我们的权重函数。我们没有给每一个邻居节点一个唯一的标签，而是通过将一个关节节点$v_{ti}$的邻居集$B(v_{ti})$分成固定的$K$个子集来简化过程，每个子集都有一个数字标签。因此，我们可以拥有一个映射$l_{ti}:B(v_{ti})\to \{0,...,K-1\}$，该映射将附近的节点映射到其子集标签。权重函数$\mathbf{w}(v_{ti},v_{tj}):B(v_{ti})\to R^c$可通过索引$(c,K)$维张量来实现，或者
  $$\mathbf{w}(v_{ti},v_{tj})={\mathbf{w}}^{\prime }(l_{ti}(v_{tj}))\text{\hspace{1em}(3)}$$
  我们将在3.4节中讨论几种分区策略。
• 空间图卷积，利用改进的采样函数和权重函数，在图卷积方面我们重写等式1：
  $$f_{out}(v_{ti})=\sum _{v_{tj}\in B(v_{ti})}\frac{1}{Z_{ti}(v_{tj})}{f}_{in}(\mathbf{p}(v_{ti},v_{tj}))\cdot \mathbf{w}(v_{ti},v_{tj})\text{\hspace{1em}(4)}$$
  归一化项$Z_{ti}(v_{vtj})=|\{v_{tk}|l_{ti}(v_{tk})=l_{ti}(v_{tj})\}|$等于相应子集的基数。加入该项是为了平衡不同子集对于输出的贡献。将等式2和等式3带入等式4，我们可以获得：
  $$f_{out}(v_{ti})=\sum _{v_{tj}\in B(v_{ti})}\frac{1}{Z_{ti}(v_{tj})}{f}_{in}(v_{tj})\cdot \mathbf{w}(l_{ti}(v_{tj}))\text{\hspace{1em}(5)}$$
  值得注意的是，如果我们将图像视为常规2D网格，则此公式可以类似于标准2D卷积。例如，类似于$3\times 3$卷积运算，我们在以像素为中心的$3\times 3$网格中有9个像素的邻居。然后应将邻居集划分为9个子集，每个子集具有一个像素。
• 时空建模，制定了空间图CNN之后，我们现在进入在骨架序列内对空间时间动态建模的任务。回想一下在图的构造中，图的时间方面是通过在连续的帧之间连接相同的关节来构造的。这使我们能够定义一个非常简单的策略来将空间图CNN扩展到空间时间域。也就是说，我们将邻居关系的概念扩展为还包含时间连接的关节：
  $$B(v_{ti})=\{v_{qj}|d(v_{tj},v_{ti})\le K,|q-t|\le \lfloor \Gamma /2\rfloor \}\text{\hspace{1em}(6)}$$
  参数$\Gamma$控制要包含在邻居图中的时间范围，因此可以称为时间内核大小。为了完成对空间时间图的卷积运算，我们还需要与空间情况相同的采样函数，以及权重函数，尤其是标签图$l_{ST}$。因为时间轴是有序的，所以我们直接针对以$v_{ti}$为根的空间时间邻域修改标签图$l_{ST}$为：
  $$l_{ST}(v_{qj})=l_{ti}(v_{tj})+(q-t+\lfloor \Gamma /2\rfloor )\times K\text{\hspace{1em}(7)}$$
  其中$l_{ti}(v_{tj})$是$v_{ti}$处单帧的标签图。这样，我们在构造的空间时间图上就有了定义明确的卷积运算。

图3.所提出的用于构造卷积运算的分区策略。从左到右：（a）输入框架的示例框架。身体关节用蓝点绘制。$D=1$的过滤器的接受范围用红色虚线圈绘制。（b）单标签分区策略，其中邻居中的所有节点都具有相同的标签（绿色）。（c）距离划分，这两个子集是距离为0的根节点本身（绿色）和距离为1的其他相邻节点（蓝色）。（d）空间配置分区，根据节点到骨架重心的距离（黑色十字）与根节点（绿色）的距离来标记节点。向心节点（蓝色）的距离短，而离心节点（黄色）的距离比根节点长

3.4 分区策略

• 给定空间时间图卷积的高级表示，设计分区策略以实现标签图$l$很重要。在这项工作中，我们探索了几种分区策略。为简单起见，我们只讨论单个帧中的情况，因为可以使用等式7将它们自然地扩展到时空域。
• 单标签，最简单，最直接的划分策略是拥有子集，即整个邻居集本身。在这种策略中，每个相邻节点上的特征向量将具有相同权重向量的内积。实际上，这种策略类似于（Kipf和Welling 2017）中引入的传播规则。明显的缺点是，在单帧的情况下，使用此策略等效于计算权重向量和所有相邻节点的平均特征向量之间的内积。对于骨架序列分类而言并不是最好的选择，因为在此操作中可能会丢失局部差分特性。形式上，我们有$K=1$和$l_{ti}(v_{tj})=0,\forall i,j\in V$。
• 距离划分，另一个自然的分区策略是根据节点到根节点$v_{ti}$的距离$d(\cdot ,v_{ti})$划分邻居集。在这项工作中，由于我们设置的$D=1$，所以邻居集将被分为两个子集，其中$d=0$的是根节点本身，其余邻居节点位于$d=1$的子集中。因此，我们将拥有两个不同的权重向量，它们能够对局部差分特性（例如关节之间的相对移动）进行建模。形式上，我们有$K=2$和$l_{ti}(v_{tj})=d(v_{tj},v_{ti})$。
• 空间配置分区，由于人体骨骼在空间上是局部的，因此我们仍可以在划分过程中利用此特定的空间配置。我们设计了一种策略，将邻居集划分为三个子集：1）根节点本身；2）向心群：比根节点更靠近骨架重心的相邻节点；3）其他的为离心组。在这里，框架中骨架所有关节的平均坐标视为重心。该策略的灵感来自以下事实：身体部位的运动可以大致分为同心运动和偏心运动。正式地，我们有：
  $$l_{ti}(v_{tj})=\{\begin{array}{llc}0& \mathrm{i}\mathrm{f}& r_j=r_i\\ 1& \mathrm{i}\mathrm{f}& r_j<r_i\\ 2& \mathrm{i}\mathrm{f}& r_j>r_i\end{array}\text{\hspace{1em}(8)}$$
  $r_i$是训练集中所有框架的上重心到关节$i$的平均距离。
• 三种分区策略的可视化效果如图3所示。我们将基于骨架的动作识别实验对提议的分区策略进行实证研究。可以估计到，更高级的分区策略将导致更好的建模能力和识别性能。

3.5 可学习的边的重要性权重

• 尽管人们在执行动作时关节会成组移动，但一个关节可能会出现在身体的多个部位。但是，在对这些部位进行动态建模时，这些应该具有不同的重要性。从这个意义上说，我们在空间时间图卷积的每一层上都添加了一个可学习的掩码$\mathbf{M}$。这个掩码会根据$E_S$中在空间图上每个边所学到的重要性权重来缩放节点的特征对其相邻节点的贡献。从经验上我们发现添加这个掩码会进一步提高ST-GCN的识别性能。同样也可能具有依赖数据的关注图。我们把这个留给以后的作品。

3.6 实施ST-GCN

• 基于图的卷积的实现不像2D或3D卷积那么简单。在此，我们提供有关为基于骨架的动作识别实现ST-GCN的详细信息。
• 我们采用与（Kipf和Welling 2017）中类似的图卷积实现。一帧内关节的体内连接由邻接矩阵$\mathbf{A}$和表示自连接的单位矩阵$\mathbf{I}$表示。在单帧情况下，具有第一种分区策略的ST-GCN可以通过以下公式实现（Kipf和Welling 2017）：
  $${\mathbf{f}}_{out}={\Lambda }^{-\frac{1}{2}}(\mathbf{A}+\mathbf{I}){\Lambda }^{-\frac{1}{2}}{\mathbf{f}}_{in}\mathbf{W}\text{\hspace{1em}(9)}$$
  这里的${\Lambda }^{ii}={\sum }_j(A^{ij}+I^{ij})$。多个输出通道的权重向量被堆叠以形成权重矩阵$\mathbf{W}$。在实践中，在时空情况下，我们可以将输入特征图表示为$(C,V,T)$维的张量。图卷积是通过执行$1\times \Gamma$标准2D卷积实现的，并将结果张量与第二维上的归一化邻接矩阵${\Lambda }^{-\frac{1}{2}}(\mathbf{A}+\mathbf{I}){\Lambda }^{-\frac{1}{2}}$相乘。
• 对于具有多个子集分区策略，即距离分区和空间配置分区，我们再次使用此实现。但是现在请注意，邻接矩阵可分解为几个矩阵${\mathbf{A}}_j$，其中$\mathbf{A}+\mathbf{I}={\sum }_j{\mathbf{A}}_j$，例如，在距离划分策略中，${\mathbf{A}}_0=\mathbf{I}和{\mathbf{A}}_1=\mathbf{A}$，等式9就变成：
  $${\mathbf{f}}_{out}=\sum _j{\Lambda }_j^{-\frac{1}{2}}{\mathbf{A}}_j{\Lambda }^{-\frac{1}{2}}{\mathbf{f}}_{in}{\mathbf{W}}_j\text{\hspace{1em}(10)}$$
  近似地我们令${\Lambda }_j^{ii}={\sum }_k(A_j^{ik})+\alpha$，这里我们将$\alpha =0.001$来避免${\mathbf{A}}_j$中出现空行的情况。
• 实施可学习的边的重要性权重很简单。对于每个邻接矩阵，我们将其与一个可学习的权重矩阵$\mathbf{M}$相伴。然后，分别用$(\mathbf{A}+\mathbf{I})\otimes \mathbf{M}$和${\mathbf{A}}_j\otimes \mathbf{M}$替换矩阵等式9中的$\mathbf{A}+\mathbf{I}$和等式10中${\mathbf{A}}_j$的$A_j$。$\otimes$表示两个矩阵之间的逐元素乘积。掩码$\mathbf{M}$初始化为全1矩阵。
• 网络的架构和训练，由于ST-GCN在不同节点上共享权重，因此在不同关节上保持输入数据的大小一致非常重要。在我们的实验中，我们首先将输入骨架输入到批处理规范化层以规范化数据。ST-GCN模型由9层时空图卷积运算符（ST-GCN单元）组成。前三层有64个输出通道。接下来的三层有128个通道用于输出。最后三层有256个通道用于输出。这些层的时间内核大小为9。Resnet机制应用于每个ST-GCN单元之后，我们以0.5的概率随机删除了这些特征，以避免过拟合。将第4和第7时间卷积层的步长设置为2作为池化层。此后，对结果张量进行全局池化，以获得每个序列的256维特征向量。最后，我们将它们提供给Softmax分类器。使用具有0.01的学习率的随机梯度下降学习模型。每隔10个周期，我们会将学习率衰减0.1。为避免过渡拟合，我们在Kinetics数据集上进行训练时执行两种扩充（Kay等人 2017）。首先，为了模拟相机的运动，我们对所有帧的骨架序列执行随机仿射变换。特别是，从第一帧到最后一帧，我们选择一些固定角度，平移和缩放因子作为候选，然后随机采样三个因子的两个组合以生成仿射变换。对中间帧进行插值转换，以产生一种效果，就好像我们在播放过程中平滑移动视点一样，我们称这种增强为随机移动。其次，我们在训练中从原始骨架序列中随机抽取片段，并在测试中使用所有帧。网络顶部的全局池化可以使网络处理长度不确定的输入序列。

4 实验

在本节中，我们评估ST-GCN在基于骨骼的动作识别实验中的性能，我们对两个性质完全不同的大型动作数据集（Kinetics）（Kay等人 2017）是至今为止最大的无约束动作识别数据集，而NTU-RGB+D（Shahroudy等人 2016）是最大的内部捕获动作识别数据集。特别是，我们首先在动力学数据集上进行了详细的消融研究，以检验提出的模型组件对识别性能的贡献。然后我们比较了使用了其他最先进的方法和其他输入方式后的ST-GCN识别结果。为了验证我们在无约束条件下获得的经验是否通用，我们在NTU-RGB+D对约束条件进行了实验，并将ST-GCN与其他最新方法进行了比较。所有实验均在带有8个TITANX GPUs的Pytorch深度学习框架上进行。ST-GCN的代码和模型已公开提供¹。

4.1 数据集和评估指标

• 动力学数据集，Deepmind Kinetics人类动作数据集（Kay等人 2017）包含从Youtube检索到的约300000个视频剪辑。这些视频涵盖了多达400种人类活动课，从日常活动，运动场景到具有交互作用的复杂动作，不一而足。Kinetics中的每个剪辑视频约为10秒，FPS为30，或总共300帧。
• 此Kinetics数据集仅提供原始视频剪辑，而没有骨骼数据。在这项工作中，我们专注于基于骨骼的动作识别，因此我们将像素坐标系中的估计联合位置用作我们的输入，并丢弃原始的RGB帧。为了获得关节的位置，我们首先将所有视频的大小调整为$340\times 256$的分辨率。然后，使用公共可用的$OpenPose$（Cao等人 2017）工具箱来估计每一帧上18个关节的位置。该工具箱在像素坐标系中给出了2D坐标$(X,Y)$并给出了18个人体关节的置信度$C$。因此，我们用$(X,Y,C)$元组表示每个关节，并将骨架框架记录为18个元组的数组。对于多人案例，我们选择每个剪辑视频中平均联合置信度最高的人。这样一个带有$T$帧的剪辑视频被转换为这些元组的骨架序列。实际上，我们用维度为$(18,3,T)$的张量表示剪辑视频。为了简单起见，我们通过从头开始重播序列以$T=300$来填充每个剪辑视频。我们将在Kinetics上发布估计的关节位置以重现结果。
• 我们根据数据集作者的建议按top-1和top-5分类准确性评估识别性能（Kay等人 2017）。数据集提供了240000个剪辑的训练集和20000的验证集。我们在训练集上训练比较的模型，并报告验证集的准确性。
• NTU-RGB+D：NTU-RGB+D（Shahroudy等人 2016）是目前最大的具有3D关节注释的数据集，用于人类动作识别任务。该数据集包含60个动作类别，一共有56000动作剪辑视频。这些视频都是由在受限实验室环境中由40名志愿者执行所捕获的，同时记录了三个摄像机视图。所给的注释提供了由Kinect深度传感器检测到的在相机坐标系中的3D关节位置$(X,Y,Z)$。骨骼序列中每个对象有25个关节。每个剪辑的视频中保证最多只有两个类别。
• 该数据集的作者推荐两个基准：1）交叉类别（X-Sub）基准，其中包含39889个和16390个剪辑视频用于训练和评估。在这里面训练的剪辑视频来自于一个演员子集。且剩下的演员的剪辑视频用来进行评估；2）交叉视角（X-View）基准测试有37462和18817个剪辑视频。这个里面的训练视频来自于摄像机视角2和3，评估视频全部来自于摄像机视角1。我们遵循这些约定，并在两个基准上报告了top-1的识别精度。

表1.动力学数据集的消融研究。ST-GCN+Imp与其他最新方法进行比较。有关每种设置的意义，请查看第4.2节。

4.2 消融研究

• 我们通过在Kinetics数据集上进行动作识别实验来检查ST-GCN中拟议组件的有效性（Kay等人 2017）。
• 空间时间图卷积，首先我们评估使用空间时间图卷积运算的必要性。我们使用基线网络架构（Kim和Reiter 2017），其中所有空间时间卷积仅通过时间卷积代替。也就是说我们将所有输入关节位置连接起来，以在每个帧$t$处形成输入特征。然后，时间卷积将对此输入进行运算，并随时间进行卷积。我们将此模型称为基线TCN。众所周知，这种识别模型可以在约束数据集上（例如NTU-RGB+D）上很好地工作（Kim和Reiter 2017）。从表1可以看出具有空间时间图卷积的模型以及合理的划分策略，始终优于Kinetics的基线模型。实际上，这种时间卷积相当于完全连接的联合图上具有未共享权重的空间时间图卷积。因此，基线模型和ST-GCN之间的主要区别是稀疏的自然连接和卷积运算中的共享权重。另外，我们评估了基线模型和ST-GCN之间的中间模型，称为局部卷积。在此模型中，我们将稀疏联合图用作ST-GCN，但使用权重不共享的卷积过滤器。我们相信基于ST-GCN的模型能够证明基于骨骼的动作识别中时空图卷积的强大能力。
• 分区策略，在这项工作中，我们提出了三种分区策略：1）单标签；2）距离划分；3）空间配置分区。我们使用这些分区策略来评估ST-GCN的性能，并且结果在表1中显示。我们发现具有多个子集的分区通常要比单标签好得多。这符合单标签的明显的问题，即等同于在卷积运算之前对特征进行平均。根据这种观察，我们尝试在距离划分和单标签之间进行一个中间操作，称为距离划分*。在此设置中，我们将距离分区中两个子集的权重绑定为仅因比例因子$-1或{\mathbf{w}}_0=-{\mathbf{w}}_1$而不同，与单标签相比，此设置仍然具有更好的性能，这再次证明了使用多个子集进行分区的重要性。在多个子集分区策略中，空间配置分区可以实现更好的性能。这证实了我们设计该策略的目的，该策略考虑了同心和离心运动模式。基于这些观察，我们在以下实验中使用空间配置分区策略。
• 可学习的边的重要性权重，ST-GCN中的另一个组件是可学习的边的重要性权重。我们尝试通过空间配置分区将该组件添加到ST-GCN模型中。这称为ST-GCN+Imp，在表1中，鉴于高性能的ST-GCN，该组件仍能将识别性能提高1%以上。回想一下这个组件的灵感在于不同部分的关节具有不同的重要性，这证明了ST-GCN模型现在可以学习表达关节的重要性并提高了识别性能。基于这个的发现，我们将在与其他最先进的模型进行比较的时候总是使用这个组件。

表2.Kinetics数据集上基于骨骼的动作识别模型。在表格的顶部，我们列出了基于框架的方法的性能。

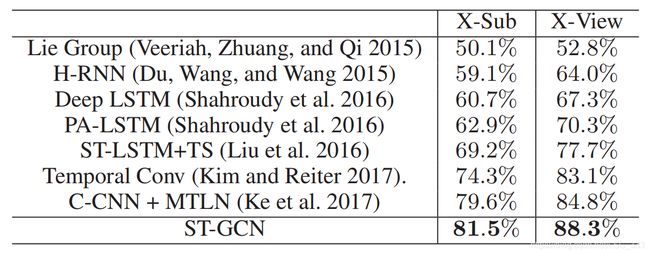
表3.在NTU-RGB+D数据集上基于骨架的动作识别性能。我们报告了交叉类别（X-Sub）和交叉视角（X-View）的准确性。

表4.Kinetics数据集的子集Kinetics Motion的均值分类精度。该子集包含30种与人体运动密切相关的运动类别。

表5.Kinetics数据集上的分类精度。尽管我们基于骨架的模型ST-GCN无法获得在RGB和光流模型上执行的最新模型的准确度，但与基于光流的模型相比，它可以提供更强大的补充信息。

4.3 与现有技术的比较

• 为了验证ST-GCN在非约束和约束环境下的性能，我们分别在Kinetics数据集（Kay等人 2017）和NTU-RGB+D数据集（Shahroudy等人 2016）上进行了实验。
• 动力学数据集，我们比较了三种基于骨骼的动作识别的特征方法。第一种是手工制作特征的特征编码法（Fernando等人 2015），在表2中称为特征编码。我们还基于Kinetics实施了两种基于深度学习的方法，即Deep LSTM（Shahroudy等人 2016）和Temporal ConvNet（Kim和Reiter 2017）。我们根据top-1和top-5的准确性比较了这些方法的识别性能。在表2中，ST-GCN能胜过以前的代表性方法。作为参考，我们列出了使用RGB帧和光流进行识别的性能（Kay等人 2017）。
• NTU-RGB+D，是在约束环境中捕获的，这使得需要稳定且状态良好的骨架序列的方法可以正常工作。我们还将ST-GCN模型与该数据集上的最新方法相比较。由于该数据集的约束性质，我们在训练ST-GCN模型时不使用任何数据扩充。我们遵循文献中的标准做法，报告是交叉分类（X-Sub）和交叉视角（X-View）在top-1分类上的准确性。比较的方法包括Lie Group（Veeriah，Zhuang和Qi 2015），Hierarchical RNN（Du，Wang和Wang 2015），Deep LSTM（Shahroudy等人 2016），Part-Aware LSTM（PA-LSTM）（Shahroudy等人 2016），Spatial Temporal LSTM with Trust Gates（ST-LSTM+TS）（Liu等人 2016），Temporal Convolutional Neural Networks（Temporal Conv）（Kim和Reiter 2017）和Clips CNN+Muti-task learning（C-CNN+MTLN）（Ke等人 2017）。我们的ST-GCN模型具有相当简单的架构，并且不使用（Kim和Reiter 2017；Ke等人 2017）进行的数据扩充，因此能够在该数据集上胜过以往的最新方法。
• 讨论，实验中的两个数据集具有非常不同的性质。在动力学数据集上，输入的是用深度神经网络检测的2D骨架（Cao等人 2017），而在NTU-RGB+D上，摄像机是固定的，而在动力学数据集上，视频通常都是由手持设备拍摄的，这会导致摄像机的运动很大。拟议的ST-GCN在两个数据集上都能很好地工作的事实证明了拟议的时空图卷积运算和所得的ST-GCN模型的有效性。
• 我们还注意到，在动力学数据集上，基于骨架的方法的准确性不如基于视频帧的模型（Kay等人 2017）。我们认为，这是由于Kinetics中的许多活动类别需要识别与演员进行交互的对象和场景。为了验证这一点，我们选择了与身体运动密切相关的30个类别的子集，称为运动学运动，并在表4中列出了基于骨架和视频帧模型的平均分类精度（Kay等人 2017）。我们可以看到，在该子集上，性能差距要小得多。我们还探索了使用ST-GCN在两流式动作识别中捕获运动信息。如表5所示，我们基于骨骼的模型ST-GCN也可以为RGB和光流模型提供补充信息。我们使用RGB和光流模型在Kinetics上训练了标准的TSN（Wang等人 2016）模型。在RGB模型中添加ST-GCN可以增加$0.9\%$，甚至比光流（$0.8\%$）还好。结合RGB，光流和ST-GCN可将性能进一步提高到$71.7\%$。这些结果清楚地表明，当有效利用（例如使用ST-GCN）时，骨骼可以提供补充信息。

5 总结

• 在本文中，我们提出了一种基于骨架的动作识别的新型模型，即时空图卷积网络（ST-GCN）。该模型在骨架序列上构造了一组空间时间图卷积。在两个具有挑战性的大规模数据集上，拟议的ST-GCN优于先前基于骨架的最新模型。另外，ST-GCN可以捕获动态的骨架序列上的运动信息，这是对于RGB模式的补充。基于骨架的模型和基于视频帧的模型的组合进一步提高了动作识别的性能。ST-GCN模型的灵活性也为将来的工作开辟了许多可能的方向。例如，如何将上下文信息（例如场景，对象和交互）整合到ST-GCN中就成为一个自然地问题。
• 致谢：这项工作得到了SenseTime集团的大数据协作研究资助（CUHK Agreement No.TS1610626），和香港的the Early Career Scheme（ECS）（No.24204215）的部分支持。

6 参考文献

• Bruna, J.; Zaremba, W.; Szlam, A.; and Lecun, Y. 2014. Spectral networks and locally connected networks on graphs. In ICLR.
• Cao, Z.; Simon, T.; Wei, S.-E.; and Sheikh, Y. 2017a. Realtime multi-person 2d pose estimation using part affinity fields. In CVPR.
• Cao, Z.; Simon, T.; Wei, S.-E.; and Sheikh, Y. 2017b. Realtime multi-person 2d pose estimation using part affinity fields. In CVPR.
• Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; and Wei, Y. 2017. Deformable convolutional networks. In arXiv:1703.06211.
• Defferrard, M.; Bresson, X.; and Vandergheynst, P. 2016. Convolutional neural networks on graphs with fast localized spectral filtering. In NIPS.
• Du, Y.; Wang, W.; and Wang, L. 2015. Hierarchical recurrent neural network for skeleton based action recognition. In CVPR, 1110–1118.
• Duvenaud, D. K.; Maclaurin, D.; Iparraguirre, J.; Bombarell, R.; Hirzel, T.; Aspuru-Guzik, A.; and Adams, R. P. 2015. Convolutional networks on graphs for learning molecular fingerprints. In NIPS.
• Fernando, B.; Gavves, E.; Oramas, J. M.; Ghodrati, A.; and Tuytelaars, T. 2015. Modeling video evolution for action recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 5378–5387.
• Henaff, M.; Bruna, J.; and LeCun, Y. 2015. Deep convolutional networks on graph-structured data. In arXiv:1506.05163.
• Hussein, M. E.; Torki, M.; Gowayyed, M. A.; and El-Saban, M. 2013. Human action recognition using a temporal hierarchy of covariance descriptors on 3d joint locations. In IJCAI.
• Kay, W.; Carreira, J.; Simonyan, K.; Zhang, B.; Hillier, C.; Vijayanarasimhan, S.; Viola, F.; Green, T.; Back, T.; Natsev, P.; et al. 2017. The kinetics human action video dataset. In arXiv:1705.06950.
• Ke, Q.; Bennamoun, M.; An, S.; Sohel, F.; and Boussaid, F. 2017. A new representation of skeleton sequences for 3d action recognition. In CVPR.
• Kim, T. S., and Reiter, A. 2017. Interpretable 3d human action analysis with temporal convolutional networks. In BNMW CVPRW.
• Kipf, T. N., and Welling, M. 2017. Semi-supervised classification with graph convolutional networks. In ICLR 2017.
• Krizhevsky, A.; Sutskever, I.; and Hinton, G. E. 2012.Imagenet classification with deep convolutional neural networks. In NIPS.
• Li, Y.; Zemel, R.; Brockschmidt, M.; and Tarlow, D. 2016. Gated graph sequence neural networks. In ICLR.
• Li, C.; Zhong, Q.; Xie, D.; and Pu, S. 2017. Skeleton-based action recognition with convolutional neural networks. In arXiv:1704.07595.
• Liu, J.; Shahroudy, A.; Xu, D.; and Wang, G. 2016. Spatiotemporal lstm with trust gates for 3d human action recognition. In ECCV, 816–833. Springer.
• Niepert, M.; Ahmed, M.; and Kutzkov, K. 2016. Learning convolutional neural networks for graphs. In International Conference on Machine Learning.
• Shahroudy, A.; Liu, J.; Ng, T.-T.; and Wang, G. 2016. Ntu rgb+ d: A large scale dataset for 3d human activity analysis. In CVPR, 1010–1019.
• Shotton, J.; Sharp, T.; Kipman, A.; Fitzgibbon, A.; Finocchio, M.; Blake, A.; Cook, M.; and Moore, R. 2011. Realtime human pose recognition in parts from single depth images. In CVPR.
• Simonyan, K., and Zisserman, A. 2014. Two-stream convolutional networks for action recognition in videos. In Advances in neural information processing systems, 568–576.
• Tai, K. S.; Socher, R.; and Manning, C. D. 2015. Improved semantic representations from tree-structured long short-term memory networks. In ACL.
• Tran, D.; Bourdev, L.; Fergus, R.; Torresani, L.; and Paluri, M. 2015. Learning spatiotemporal features with 3d convolutional networks. In Proceedings of the IEEE international conference on computer vision, 4489–4497.
• Van Oord, A.; Kalchbrenner, N.; and Kavukcuoglu, K. 2016. Pixel recurrent neural networks. In ICML.
• Veeriah, V.; Zhuang, N.; and Qi, G.-J. 2015. Differential recurrent neural networks for action recognition. In CVPR, 4041–4049.
• Vemulapalli, R.; Arrate, F.; and Chellappa, R. 2014. Human action recognition by representing 3d skeletons as points in a lie group. In CVPR, 588–595.
• Wang, J.; Liu, Z.; Wu, Y.; and Yuan, J. 2012. Mining actionlet ensemble for action recognition with depth cameras. In CVPR. IEEE.
• Wang, L.; Xiong, Y.; Wang, Z.; Qiao, Y.; Lin, D.; Tang, X.; and Val Gool, L. 2016. Temporal segment networks: Towards good practices for deep action recognition. In ECCV.
• Wang, L.; Qiao, Y.; and Tang, X. 2015. Action recognition with trajectory-pooled deep-convolutional descriptors. In Proceedings of the IEEE conference on computer vision and pattern recognition, 4305–4314.
• Zhang, S.; Liu, X.; and Xiao, J. 2017. On geometric features for skeleton-based action recognition using multilayer lstm networks. In WACV. IEEE.
• Zhao, Y.; Xiong, Y.; Wang, L.; Wu, Z.; Tang, X.; and Lin, D. 2017. Temporal action detection with structured segment networks. In ICCV.
• Zhu, W.; Lan, C.; Xing, J.; Zeng, W.; Li, Y.; Shen, L.; Xie, X.; et al. 2016. Co-occurrence feature learning for skeleton based action recognition using regularized deep lstm networks. In AAAI.

---

1. https://github.com/yysijie/st-gcn ↩︎