点云关键点、对应关系、热力图可视化总结

点云可视化常用的库是open3d，其中关于关键点、对应关系、热力图的可视化却几乎没有博客讲解，本文填补这一空缺，为点云配准的研究工作提供便利

关键点可视化

关键点可以在显著图上采样得到，使用keypoints_to_spheres函数可以可以绘制出球状的关键点，其中radius参数控制球的半径

import torch
import open3d as o3d
import numpy as np


def sample_interest_points(method, scores, N):
    """
    We can do random sampling, probabilistic sampling, or top-k sampling
    """
    assert method in ['prob', 'topk', 'random']
    n = scores.size
    if n < N:
        choice = np.random.choice(n, N)
    else:
        if method == 'random':
            choice = np.random.permutation(n)[:N]
        elif method == 'topk':
            choice = torch.topk(torch.from_numpy(scores), N, dim=0)[1].numpy()
        elif method == 'prob':
            idx = np.arange(n)
            probs = (scores / scores.sum()).flatten()
            choice = np.random.choice(idx, size=N, replace=False, p=probs)

    return choice


def keypoints_to_spheres(keypoints, color):
    spheres = o3d.geometry.TriangleMesh()
    for keypoint in keypoints.points:
        sphere = o3d.geometry.TriangleMesh.create_sphere(radius=0.015)
        sphere.translate(keypoint)
        spheres += sphere
    if color == 1:
        spheres.paint_uniform_color([1, 0, 0])
    else:
        spheres.paint_uniform_color([0, 0, 1])
    return spheres


if __name__ == '__main__':
    src_raw = np.load('../src_raw_19.npy')
    # scores = np.load('../scores.npy')
    M, _ = src_raw.shape
    scores = np.random.uniform(0,1,M)
    src_idx = sample_interest_points('prob', scores, 500)
    src_keypts = src_raw[src_idx]

    raw1 = o3d.geometry.PointCloud()
    raw1.points = o3d.utility.Vector3dVector(src_raw)
    raw1.estimate_normals()
    radii = [0.005, 0.01, 0.02, 0.04]
    rec_mesh1 = o3d.geometry.TriangleMesh.create_from_point_cloud_ball_pivoting(
        raw1, o3d.utility.DoubleVector(radii))
    raw1.paint_uniform_color([107/255, 175/255, 214/255])


    keypts1 = o3d.geometry.PointCloud()
    keypts1.points = o3d.utility.Vector3dVector(src_keypts)
    mesh_box1 = keypoints_to_spheres(keypts1, 1)

    o3d.visualization.draw_geometries([raw1, rec_mesh1, mesh_box1])

对应关系可视化

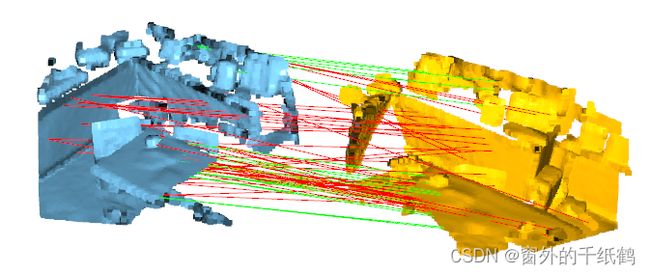
建立对应关系（correspondences）是点云配准的重要步骤，可以通过匹配算法（如最近邻匹配，ransac, sinkhorn）等方法得到对应关系。我们通常希望直观看到我们预测的对应关系有哪些是正确的，哪些是错误的。真值可以根据变换矩阵变换点云之后判断对应点，下图中绿色线代表正确对应关系，红色线代表错误对应关系。

import glob,os
import open3d as o3d
import numpy as np
import torch
from matplotlib import cm

def sample_interest_points(method, scores, N):
    """
    We can do random sampling, probabilistic sampling, or top-k sampling
    """
    assert method in ['prob', 'topk', 'random']
    n = scores.size
    if n < N:
        choice = np.random.choice(n, N)
    else:
        if method == 'random':
            choice = np.random.permutation(n)[:N]
        elif method == 'topk':
            choice = torch.topk(torch.from_numpy(scores), N, dim=0)[1].numpy()
        elif method == 'prob':
            idx = np.arange(n)
            probs = (scores / scores.sum()).flatten()
            choice = np.random.choice(idx, size=N, replace=False, p=probs)

    return choice

def keypoints_to_spheres(keypoints, color):
    spheres = o3d.geometry.TriangleMesh()
    for keypoint in keypoints.points:
        sphere = o3d.geometry.TriangleMesh.create_sphere(radius=0.050)
        sphere.translate(keypoint)
        # sphere.paint_uniform_color(color[i])
        spheres += sphere
    # spheres.vertex_colors = o3d.utility.Vector3dVector(color)
    spheres.paint_uniform_color(color)

    return spheres

src_raw = np.load('../src_raw.npy')
tgt_raw = np.load('../tgt_raw.npy')
src_pcd = np.load('../src_pcd.npy')[:70]
tgt_pcd = np.load('../tgt_pcd.npy')[:70]
gt = np.load('../gt.npy')

src_raw = src_raw.dot(gt[:3,:3].T) + gt[:3,3]
src_pcd = src_pcd.dot(gt[:3,:3].T) + gt[:3,3]
# 拉大点云距离，方便可视化
delta = [3,0.2,0.5]
src_raw += delta
src_pcd += delta
# 可视化关键点和源点云
pcd1 = o3d.geometry.PointCloud()
pcd1.points = o3d.utility.Vector3dVector(src_raw)
pcd1.estimate_normals()
radii = [0.005, 0.01, 0.02, 0.04]
rec_mesh1 = o3d.geometry.TriangleMesh.create_from_point_cloud_ball_pivoting(
    pcd1, o3d.utility.DoubleVector(radii))
pcd1.paint_uniform_color([249/255, 180/255, 2/255])

pcd2 = o3d.geometry.PointCloud()
pcd2.points = o3d.utility.Vector3dVector(tgt_raw)
pcd2.estimate_normals()
radii = [0.005, 0.01, 0.02, 0.04]
rec_mesh2 = o3d.geometry.TriangleMesh.create_from_point_cloud_ball_pivoting(
    pcd1, o3d.utility.DoubleVector(radii))
pcd2.paint_uniform_color([107 / 255, 175 / 255, 214 / 255])

# 画线
frag = np.concatenate([src_pcd, tgt_pcd], 0)
n = src_pcd.shape[0]
lines = np.zeros([n, 2])
lines[:, 0] = np.linspace(0, n - 1, n)
lines[:, 1] = np.linspace(0, n - 1, n) + n
line_set = o3d.geometry.LineSet(
    points=o3d.utility.Vector3dVector(frag),
    lines=o3d.utility.Vector2iVector(lines),
)
# 判断哪些是正确的线
src_points_T = src_pcd - delta
mask = np.sum((src_points_T - tgt_pcd)**2,axis=1) < 0.1
colors = np.zeros((n,3))
colors[mask] = [0,255,0]
colors[~mask] = [255,0,0]
line_set.colors = o3d.utility.Vector3dVector(colors)

# 可视化对应关系
o3d.visualization.draw_geometries([pcd1,pcd2,line_set])

热力图可视化

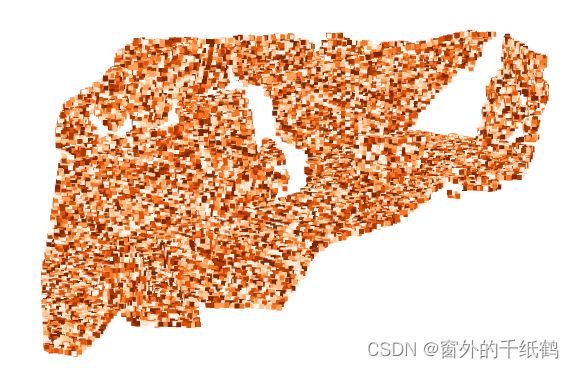
点云热力图即根据每个点的取值赋予其相应的颜色，整体上形成一个颜色分布图。比如当我求得了显著性的分布图(M $\times$ 1维)，则可以使用cm.get_cmap函数计算其颜色，又或者当求得特征图时(M $\times$ 32维)，需要先用tsne降维到(M $\times$ 1)，再用同样流程可视化。

import open3d as o3d
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from sklearn.manifold import TSNE


def make_open3d_point_cloud(xyz, color=None):
    pcd = o3d.geometry.PointCloud()
    pcd.points = o3d.utility.Vector3dVector(xyz)
    if color is not None:
        pcd.colors = o3d.utility.Vector3dVector(color)
    return pcd

def get_color_map(x):
    # colours = plt.cm.Spectral(x)
    viridis = cm.get_cmap('Oranges', 8)
    colours = viridis(x).squeeze()
    return colours[:, :3]

def embed_tsne(data):
    """
    N x D np.array data
    """
    tsne = TSNE(n_components=1, verbose=1, perplexity=40, n_iter=300, random_state=1)
    tsne_results = tsne.fit_transform(data)
    tsne_results = np.squeeze(tsne_results)
    tsne_min = np.min(tsne_results)
    tsne_max = np.max(tsne_results)
    return (tsne_results - tsne_min) / (tsne_max - tsne_min)


if __name__ == '__main__':
    show_saliency = True
    show_feature = False
    xyzr0 = np.load('../src_raw_19.npy')
    M, _ = xyzr0.shape

    if show_saliency:
        # 每个点有一个显著性得分，可视化显著性热力图
        # scores = np.load('../data/scores.npy')
        scores = np.random.uniform(0,1,M)
    elif show_feature:
        # 每个点有一个特征向量，则先用tsne降维，再可视化
        # feature = np.load('../data/feature.npy')
        feature = np.random.rand(M, 32)
        scores = embed_tsne(feature)
    else:
        scores = None
        exit()

    scores = (scores - np.min(scores)) / (np.max(scores) - np.min(scores))
    color = get_color_map(scores)

    pcd = make_open3d_point_cloud(xyzr0, color)
    o3d.visualization.draw_geometries([pcd])

以下展示随机生成一个显著性图的热力图可视化结果：