数据集:波士顿地区房价预测
数据集:波士顿地区房价预测
数据集下载地址
本文以线性回归模型预测为主
1. 数据集说明
| 变量名 | 变量描述 |
|---|---|
| CRIM | 城镇人均犯罪率 |
| ZN | 住宅地超过25000平方英尺的比例 |
| INDUS | 城镇非零售商用土地的比例 |
| CHAS | 查理斯河空变量(如果边界是河流,则为1,否则为0) |
| NOX | 一氧化碳浓度 |
| RM | 住宅平均房间数 |
| AGE | 1940年之前建成的自用房屋比例 |
| DIS | 到波士顿五个中心区区域的加权距离 |
| RAD | 辐射性公路的接近指数 |
| TAX | 每10000美元的全值财产产税率 |
| PTRATIO | 城镇师生比例 |
| B | 城镇中黑人的比例 |
| LSTAT | 人口中地位低下者的比例 |
| target | 自住房的平均房价,以千美元计 |
2. 获取数据集
# 导包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 导入数据
Boston = pd.read_csv('波士顿房价数据集.csv')
head = Boston.head()
3. 数据探索
# 采用info查看数据集信息
Boston.info()
结果:
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 506 entries, 0 to 505
Data columns (total 14 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 CRIM 506 non-null float64
1 ZN 506 non-null float64
2 INDUS 506 non-null float64
3 CHAS 506 non-null int64
4 NOX 506 non-null float64
5 RM 506 non-null float64
6 AGE 506 non-null float64
7 DIS 506 non-null float64
8 RAD 506 non-null int64
9 TAX 506 non-null int64
10 PTRATIO 506 non-null float64
11 B 506 non-null float64
12 LSTAT 506 non-null float64
13 target 506 non-null float64
dtypes: float64(11), int64(3)
memory usage: 55.5 KB
结论:
数据总共有506行,14个变量,而且这14个变量都有506个非空的float64类型的数值,即所有变量没有空值。
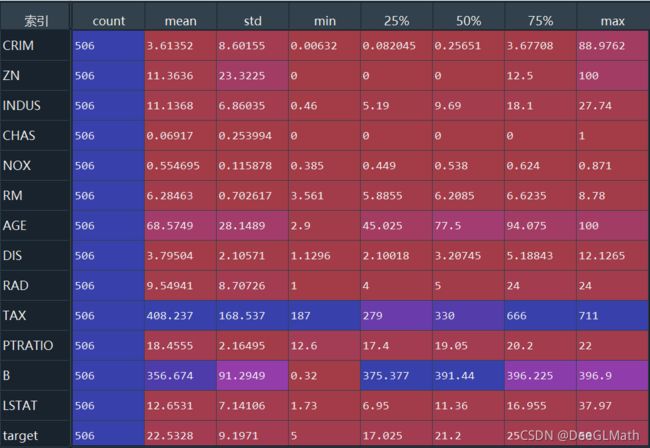
3.1 描述性统计分析
# 描述性统计分析
describe = Boston.describe().T
print(describe)
结论:
没有发现异常情况,但是可能有变量存在极端值的情况,会直接影响后续模型的开发,所以需要通过散点图直接看各个自变量与因变量的关系。
3.2 散点图分析
3.2.1 绘制犯罪率与房价散点图
# 散点图分析
def drawing(x,y,xlabel):
plt.scatter(x,y)
plt.title('%s - House Prices'% xlabel)
plt.xlabel(xlabel)
plt.ylabel('House Prices')
plt.yticks(range(0,60,5))
plt.grid()
plt.show()
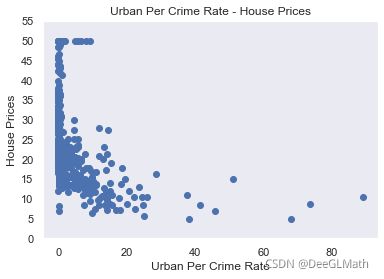
# 绘制变量CRIM和因变量的散点图
drawing(Boston['CRIM'],Boston['target'],'Urban Per Crime Rate')
结论:
从散点图的数据分布可以看出,房价基本和犯罪率呈负相关的关系,高房价的房屋都集中在低犯罪率地区,如果城镇人均犯罪率超过20%的情况,房价最高不高于20。
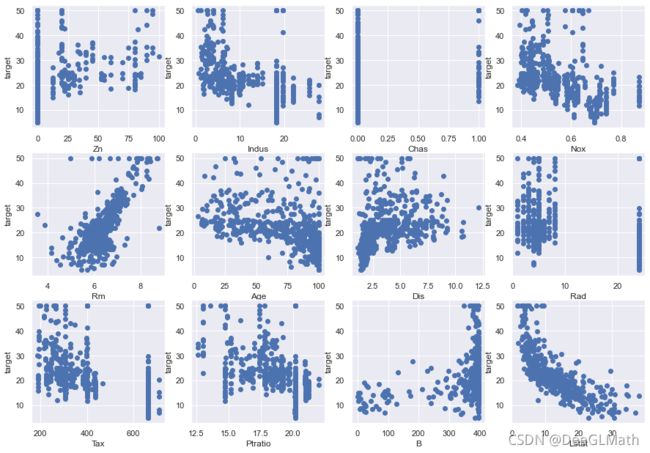
3.2.2 绘制其他所有自变量与因变量target的散点图
plt.figure(figsize=(15,10.5))
plot_count = 1
for feature in list(Boston.columns)[1:13]:
plt.subplot(3,4,plot_count)
plt.scatter(Boston[feature],Boston['target'])
plt.xlabel(feature.replace('_',' ').title())
plt.ylabel('target')
plot_count += 1
plt.show()
结论:
- ZN表示住宅用地所占比例,从散点图可以看出,其与因变量target并没有明显的线性关系
- INDUS表示城镇中非商业用地所占比例,当城镇中非商业用地所占比例处于(0,5)区间的情况下,房价不低于15
- CHAS表示地产是否处于查尔斯河边,1表示在河边,0表示不在河边,地产不在查尔斯河边的情况下,房价处于(5,55)区间,地产在查尔斯河边的情况下,房价最低不低于10
- NOX表示一氧化碳的浓度,整体看NOX与因变量target具有负的相关关系
- RM表示每栋住宅的房间数,很明显两者之间存在较强的线性关系。
- AGE表示1940年之前建成的业主自住单位的占比,自住单位的占比处于(0,60)的情况下,房价最底不会低于15.
- DIS表示距离5个波士顿就业中心的平均距离,一般来说距离就业中心近则上下班距离近,人更愿意住在上下班距离近的地方,根据市场规律,需求高则房价会高,从散点图的数据分布来看,整体与因变量target呈负的相关关系。
- RAD表示距离高速公路的接近指数,绝大多数房价高于30的房产,都集中在距离高速公路的接近指数低的地区。
- TAX表示每一万美元的不动产产税率,在税率大于600的情况下,房价会低于10。
- PTRATIO表示城镇中学生教师比例,学生教师比例小于14的情况下,房价最低不低于20,绝大部分高于30,只有在学生教师比例大于20的情况下,房价会低于10,绝大部分不高于30.
- B表示城镇中黑人比例,在黑人比例高于350的地区,房价会高于30.
- LSTAT表示低收入阶层占比,从散点图看,很明显与因变量target具有负的相关关系。
3.3 相关性分析
由于数据集中有很多个变量,我们不希望用所有变量来训练我们的模型,从散点图的数据分布上可以了解它们并不都是相关的,相反,我们希望选择那些直接影响因变量的变量来训练模型,为此,可以使用corr函数来计算变量之间的相关系数,以便判断变量之间的相关程度。
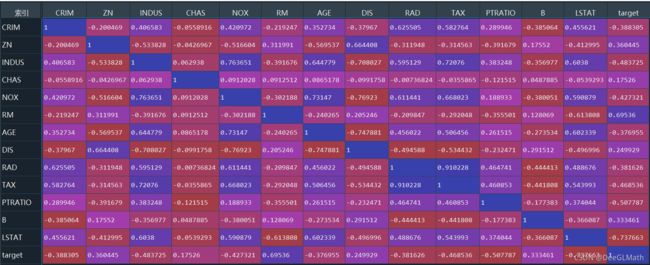
# 相关系数计算
corr = Boston.corr()
print(corr)
# 绘制相关矩阵图形
import seaborn as sn
varcorr = Boston[Boston.columns].corr()
mask = np.array(varcorr)
mask[np.tril_indices_from(mask)] = False
sn.heatmap(varcorr,mask=mask,vmax=0.8,square=True,annot=False)
图示:
热力图:
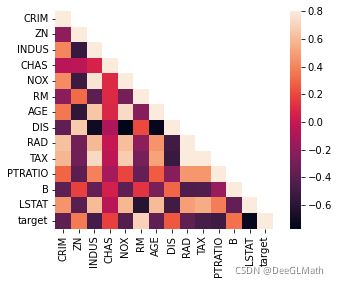
结论:
与因变量target相关程度最高的三个变量是LSTAT、RM、PTRATIO,通过如下程序获取相关程度最大的变量列表:
# 获取相关程度最大的三个变量
print(Boston.corr().abs().nlargest(4,'target').index)
结果:
Index(['target', 'LSTAT', 'RM', 'PTRATIO'], dtype='object')
根据变量之间相关程度的结果,我们可以选取上述三个自变量进入模型训练之中。
4. 建立模型
首先我们创建两个数据帧X和Y,其中数据帧X将包含LSTAT、RM、PTRATIO变量,而数据帧将包含因变量target:
# 创建两个数据帧X和Y
X = pd.DataFrame(np.c_[Boston['LSTAT'],Boston['RM'],Boston['PTRATIO']],columns=['LSTAT','RM','PTRATIO'])
Y = Boston['target']
对数据集进行分割,其中的80%用于训练模型,其他20%用于测试模型效果:
# 对数据集进行分割
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size = 0.2,random_state=5)
直接调用sklearn中的线性回归包进行模型拟合:
# 调用线性回归库进行模型拟合
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train,y_train)
打印模型的截距:
# 打印模型的截距
print(model.intercept_)
结果:
23.68107026871482
打印参数的估计系数:
# 打印出参数的估计系数
coeffcients = pd.DataFrame([X_train.columns,model.coef_]).T
coeffcients = coeffcients.rename(columns={0:'Attribute',1:'Coeffcients'})
结果:
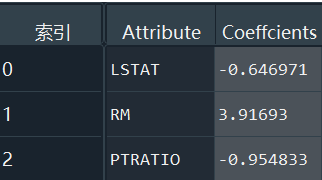
得到线性回归方程如下:
t a r g e t = 23.68107026871482 − 0.646971 × L S T A T + 3.91693 × R M − 0.954833 × P T R A T I O target=23.68107026871482-0.646971 \times LSTAT+3.91693 \times RM-0.954833 \times PTRATIO target=23.68107026871482−0.646971×LSTAT+3.91693×RM−0.954833×PTRATIO
5. 模型评估
5.1 R方检验
模型拟合完成之后,可以对模型进行测试评估,为了了解拟合的模型的效果,可以使用R方进行衡量,R方主要用来评估数据与回归数据的拟合程度,R方的值越接近1,则表示该模型拟合得越好:
# 评估模型
print('R-Squared: %.4f'% model.score(X_test, y_test))
结果:
R-Squared: 0.6916
从结果可以知道,本次模型训练得到的结果良好。
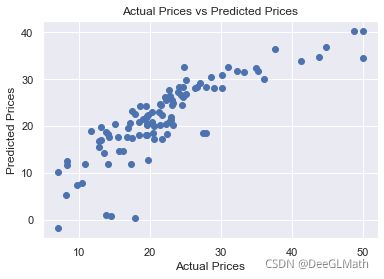
5.2 散点图检验
# 绘制预测值与实际值的散点图
plt.figure()
price_pred = model.predict(X_test)
plt.scatter(y_test,price_pred)
plt.xlabel('Actual Prices')
plt.ylabel('Predicted Prices')
plt.title('Actual Prices vs Predicted Prices')
plt.show()
虽然R方的值为0.6916,但是拟合效果不是很好,再仔细观察图的数据分布情况,在实际值为50时有离群点,因此我们需要进一步查看因变量target的直方图,诊断数据分布是否异常:
from scipy import stats
sn.distplot(Boston['target'],hist=True);
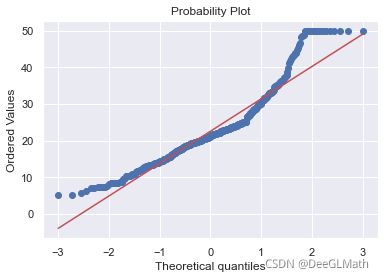
fig = plt.figure()
res = stats.probplot(Boston['target'],plot=plt)
从上述两图可以看出,因变量取值为50时为离散值,较为异常,对拟合模型的效果有重大的影响,所以必须删除取值为50的观测样本,之后在进行模型拟合:
# 删除因变量值为50的点
Boston_new = Boston[Boston['target']<50]
Boston_new.info()
X_new = pd.DataFrame(np.c_[Boston_new['LSTAT'],Boston_new['RM'],Boston_new['PTRATIO']],columns=['LSTAT','RM','PTRATIO'])
y_new = Boston_new['target']
X_new_train,X_new_test,y_new_train,y_new_test = train_test_split(X_new,y_new,test_size = 0.2,random_state=5)
model = LinearRegression()
model.fit(X_new_train,y_new_train)
print('R-Squared: %.4f'% model.score(X_new_test, y_new_test))
结果:
R-Squared: 0.7571
数据质量的好坏直接决定模型的最终拟合效果
6. 完整代码
# 导包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sn
sn.set()
# 从sklearn中导入波士顿房价数据集
# from sklearn.datasets import load_boston
# dataset = load_boston()
# # 查看数据集的信息
# print(dataset.data)
# # 查看数据集各个变量的名称
# print(dataset.feature_names)
Boston = pd.read_csv('波士顿房价数据集.csv')
head = Boston.head()
# 构建表格
# Boston = pd.DataFrame(dataset.data,columns=dataset.feature_names)
# 采用info查看数据集信息
Boston.info()
# 描述性统计分析
describe = Boston.describe().T
print(describe)
# 散点图分析
def drawing(x,y,xlabel):
plt.scatter(x,y)
plt.title('%s - House Prices'% xlabel)
plt.xlabel(xlabel)
plt.ylabel('House Prices')
plt.yticks(range(0,60,5))
plt.grid()
plt.show()
# 绘制变量CRIM和因变量的散点图
drawing(Boston['CRIM'],Boston['target'],'Urban Per Crime Rate')
plt.figure(figsize=(15,10.5))
plot_count = 1
for feature in list(Boston.columns)[1:13]:
plt.subplot(3,4,plot_count)
plt.scatter(Boston[feature],Boston['target'])
plt.xlabel(feature.replace('_',' ').title())
plt.ylabel('target')
plot_count += 1
plt.show()
# 相关系数计算
corr = Boston.corr()
print(corr)
# 绘制相关矩阵图形
varcorr = Boston[Boston.columns].corr()
mask = np.array(varcorr)
mask[np.tril_indices_from(mask)] = False
sn.heatmap(varcorr,mask=mask,vmax=0.8,square=True,annot=False)
# 获取相关程度最大的三个变量
print(Boston.corr().abs().nlargest(4,'target').index)
# 创建两个数据帧X和Y
X = pd.DataFrame(np.c_[Boston['LSTAT'],Boston['RM'],Boston['PTRATIO']],columns=['LSTAT','RM','PTRATIO'])
y = Boston['target']
# 对数据集进行分割
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size = 0.2,random_state=5)
# 调用线性回归库进行模型拟合
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train,y_train)
# 打印模型的截距
print(model.intercept_)
# 打印出参数的估计系数
coeffcients = pd.DataFrame([X_train.columns,model.coef_]).T
coeffcients = coeffcients.rename(columns={0:'Attribute',1:'Coeffcients'})
# 评估模型
print('R-Squared: %.4f'% model.score(X_test, y_test))
# 绘制预测值与实际值的散点图
plt.figure()
price_pred = model.predict(X_test)
plt.scatter(y_test,price_pred)
plt.xlabel('Actual Prices')
plt.ylabel('Predicted Prices')
plt.title('Actual Prices vs Predicted Prices')
plt.show()
# 绘制数据分布直方图及正态概率图
from scipy import stats
sn.distplot(Boston['target'],hist=True);
fig = plt.figure()
res = stats.probplot(Boston['target'],plot=plt)
# 删除因变量值为50的点
Boston_new = Boston[Boston['target']<50]
Boston_new.info()
X_new = pd.DataFrame(np.c_[Boston_new['LSTAT'],Boston_new['RM'],Boston_new['PTRATIO']],columns=['LSTAT','RM','PTRATIO'])
y_new = Boston_new['target']
X_new_train,X_new_test,y_new_train,y_new_test = train_test_split(X_new,y_new,test_size = 0.2,random_state=5)
model = LinearRegression()
model.fit(X_new_train,y_new_train)
print('R-Squared: %.4f'% model.score(X_new_test, y_new_test))