论文复现:Seam Carving for Content-Aware Image Resizing
一、论文介绍
Seam Carving for Content-Aware Image Resizing这篇论文中介绍了一种内容感知的图像调整大小的方法,通过删除或插入图像中不重要的像素点来达到图像调整大小的目的,同时使图像中的重要信息未经改变的保留下来。
如上图所示,要将左图的长宽调整到右边两张图像的大小,即宽度减小、长度增加。右下图是使用标准缩放来对图像大小进行调整,很明显图像效果非常奇怪。右上图使用的是论文中的算法,可以看到初始图像中的重要信息(建筑物、石头以及水中倒影)都被未经改变的保留了下来,使得右上图非常自然,没有什么违和感。
二、算法原理
1.定义图像中的重要信息
直观来看,与图像融合得较好的部分是图像的不重要信息,与周围像素点融合得不好即变化比较大的部分是图像的重要信息。也就是说,可以用某个位置与周边位置像素的变化率来描述该位置信息的重要性。
梯度向量的幅度值用来表示灰度的变化率,可以应用在这里。梯度向量的幅度值可以用下式近似:
▽ f = ∣ ∂ f ∂ x ∣ + ∣ ∂ f ∂ y ∣ \bigtriangledown f=\left | \frac{\partial f }{\partial x} \right | +\left | \frac{\partial f }{\partial y} \right | ▽f=∣∣∣∣∂x∂f∣∣∣∣+∣∣∣∣∂y∂f∣∣∣∣
即论文所述的能量函数:
e ( I ) = ∣ ∂ ∂ x I ∣ + ∣ ∂ ∂ y I ∣ e(I)=\left | \frac{\partial }{\partial x } I \right | +\left | \frac{\partial }{\partial y } I \right | e(I)=∣∣∣∣∂x∂I∣∣∣∣+∣∣∣∣∂y∂I∣∣∣∣
S o b e l Sobel Sobel算子可以用来近似计算图像函数在某一个像素点处对 x x x和 y y y的偏导数,因此可以在这里用来近似计算能量函数。
S o b e l Sobel Sobel模板如下图所示:
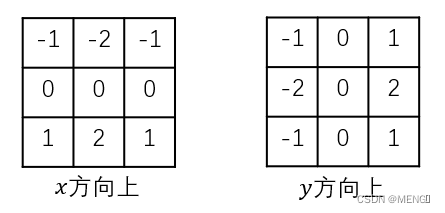
I x ( i , j ) = ( + 1 , − 1 ) + 2 ( + 1 , ) + ( + 1 , + 1 ) − ( − 1 , − 1 ) − 2 ( − 1 , ) − ( − 1 , + 1 ) I ( i + 1 , j − 1 ) + 2 I ( i + 1 , j ) + I ( i + 1 , j + 1 ) − I ( i − 1 , j − 1 ) − 2 I ( i − 1 , j ) − I ( i − 1 , j + 1 ) I_{x}(i,j)=(+1,−1)+2(+1,)+(+1,+1)−(−1,−1)−2(−1,)−(−1,+1)I(i+1, j-1)+2 I(i+1, j)+I(i+1, j+1)-I(i-1, j-1)-2 I(i-1, j)-I(i-1, j+1) Ix(i,j)=I(i+1,j−1)+2I(i+1,j)+I(i+1,j+1)−I(i−1,j−1)−2I(i−1,j)−I(i−1,j+1)I(i+1,j−1)+2I(i+1,j)+I(i+1,j+1)−I(i−1,j−1)−2I(i−1,j)−I(i−1,j+1)
I y ( i , j ) = ( − 1 , − 1 ) + 2 ( , − 1 ) + ( + 1 , − 1 ) − ( − 1 , + 1 ) − 2 ( − 1 , + 1 ) − ( + 1 , + 1 ) I ( i − 1 , j − 1 ) + 2 I ( i , j − 1 ) + I ( i + 1 , j − 1 ) − I ( i − 1 , j + 1 ) − 2 I ( i − 1 , j + 1 ) − I ( i + 1 , j + 1 ) I_{y}(i,j)=(−1,−1)+2(,−1)+(+1,−1)−(−1,+1)−2(−1,+1)−(+1,+1)I(i-1, j-1)+2 I(i, j-1)+I(i+1, j-1)-I(i-1, j+1)-2 I(i-1, j+1)-I(i+1, j+1) Iy(i,j)=I(i−1,j−1)+2I(i,j−1)+I(i+1,j−1)−I(i−1,j+1)−2I(i−1,j+1)−I(i+1,j+1)I(i−1,j−1)+2I(i,j−1)+I(i+1,j−1)−I(i−1,j+1)−2I(i−1,j+1)−I(i+1,j+1)
要求像素点 ( i , j ) (i,j) (i,j)处的能量函数:
e ( i , j ) = ∣ I x ( i , j ) ∣ + ∣ I y ( i , j ) ∣ e(i,j)=\left | I_{x}(i,j) \right | +\left | I_{y}(i,j) \right | e(i,j)=∣Ix(i,j)∣+∣Iy(i,j)∣
vector<vector<double>> GetEnergy(Image image) {
vector<vector<double>> grayvalues;
vector<double> grayvalue;
vector<vector<double>> energy;
for (int i = 0; i < image.h; i++) {
grayvalue.clear();
for (int j = 0; j < image.w; j++) {
double gray_value = image.colors[i][j][0] * 0.299 + image.colors[i][j][1] * 0.587 + image.colors[i][j][2] * 0.114;
grayvalue.push_back(gray_value);
}
grayvalues.push_back(grayvalue);
}
vector<double> raw_energy;
int x[] = { -1,-2,-1,0,0,0,1,2,1 };
vector<int> x_sobel(x, x + 9);
int y[] = { -1,0,1,-2,0,2,-1,0,1 };
vector<int> y_sobel(y, y + 9);
for (int i = 0; i < image.h; i++) {
raw_energy.clear();
for (int j = 0; j < image.w; j++) {
vector<Vec2i> ij_neighborpos = image.GetNeighborsOf(i, j);
vector<double> ij_neighborgrayvalue;
for (int k = 0; k < ij_neighborpos.size(); k++) {
if (ij_neighborpos[k][0] < 0 || ij_neighborpos[k][0] >= image.h || ij_neighborpos[k][1] < 0 || ij_neighborpos[k][1] >= image.w)
ij_neighborgrayvalue.push_back(0);
else {
double neighborgray = grayvalues[ij_neighborpos[k][0]][ij_neighborpos[k][1]];
ij_neighborgrayvalue.push_back(neighborgray);
}
}
double ex = 0;
double ey = 0;
for (int k = 0; k < 9; k++) {
double e_x = x_sobel[k] * ij_neighborgrayvalue[k];
double e_y = y_sobel[k] * ij_neighborgrayvalue[k];
ex += e_x;
ey += e_y;
}
double e = abs(ex) + abs(ey);
raw_energy.push_back(e);
}
energy.push_back(raw_energy);
}
return energy;
}
2.找到最佳接缝路径
(1).路径成本
定义接缝路径 s s s的成本是该路径上所有的像素点能量函数之和:
M ( s ) = ∑ i = 1 n e ( i , j ) M(s)=\sum_{i=1}^{n} e(i,j) M(s)=i=1∑ne(i,j)
而寻找最优接缝路径就是最小化 M ( s ) M(s) M(s),这里使用动态规划的思想来求最优接缝路径。从图像的第二行开始,遍历每一个像素点到最后一行,计算每一个像素点可能连接的路径的最小累积能量 M M M, M ( i , j ) M(i,j) M(i,j)表示从第一行到第 i i i行第 j j j列的像素点的最优路径的累积能量值:
M ( i , j ) = e ( i , j ) + m i n { M ( i − 1 , j − 1 ) , M ( i − 1 , j ) , M ( i − 1 , j + 1 ) } M(i,j)=e(i,j)+min\left \{ M(i-1,j-1),M(i-1,j),M(i-1,j+1) \right \} M(i,j)=e(i,j)+min{M(i−1,j−1),M(i−1,j),M(i−1,j+1)}
这样我们就能得到一个与图像等尺寸的路径成本 M M M集合。
vector<vector<double>> GetCost(Image image, vector<vector<double>> energy) {
vector<vector<double>> M;
M.resize(image.h);
for (int i = 0; i < image.h; i++)
M[i].resize(image.w);
for (int i = 0; i < image.w; i++)
M[0][i] = energy[0][i];
for (int i = 1; i < image.h; i++) {
for (int j = 0; j < image.w; j++) {
if (j == 0) {
if (M[i - 1][j] < M[i - 1][j + 1])
M[i][j] = energy[i][j] + M[i - 1][j];
else
M[i][j] = energy[i][j] + M[i - 1][j + 1];
}
else if (j == image.w - 1) {
if (M[i - 1][j - 1] < M[i - 1][j])
M[i][j] = energy[i][j] + M[i - 1][j - 1];
else
M[i][j] = energy[i][j] + M[i - 1][j];
}
else {
if (M[i - 1][j - 1] <= M[i - 1][j] && M[i - 1][j - 1] <= M[i - 1][j + 1])
M[i][j] = energy[i][j] + M[i - 1][j - 1];
else if (M[i - 1][j] <= M[i - 1][j - 1] && M[i - 1][j] <= M[i - 1][j + 1])
M[i][j] = energy[i][j] + M[i - 1][j];
else if (M[i - 1][j + 1] <= M[i - 1][j - 1] && M[i - 1][j + 1] <= M[i - 1][j])
M[i][j] = energy[i][j] + M[i - 1][j + 1];
}
}
}
return M;
}
(2)记录路径上的像素点
我们计算了路径成本,得到了以每一个像素点为顶点的最优路径的累积能量值,那么我们从最后一行开始,层层向上回溯,就可以得到这条最优路径所经过的所有像素点。为了便于回溯,我们可以记录得到每一个最小累积能量值 M M M的上一像素点坐标。
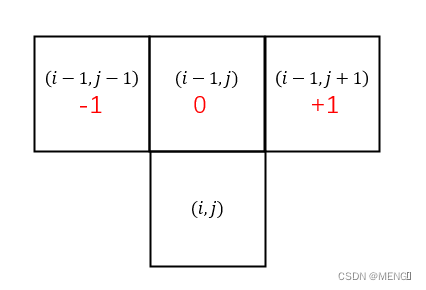
如上图所示, − 1 -1 −1表示像素点 ( i , j ) (i,j) (i,j)的上一路径坐标是 ( i − 1 , j − 1 ) (i-1,j-1) (i−1,j−1), 0 0 0表示像素点 ( i , j ) (i,j) (i,j)的上一路径坐标是 ( i − 1 , j ) (i-1,j) (i−1,j), + 1 +1 +1表示像素点 ( i , j ) (i,j) (i,j)的上一路径坐标是 ( i − 1 , j + 1 ) (i-1,j+1) (i−1,j+1)。
vector<vector<int>> FindPath(Image image, vector<vector<double>> M) {
vector<vector<int>> path;
vector<int> xpath;
for (int i = 0; i < image.w; i++)
xpath.push_back(1999);
path.push_back(xpath);
for (int i = 1; i < image.h; i++) {
xpath.clear();
for (int j = 0; j < image.w; j++) {
if (j == 0) {
if (M[i - 1][j] < M[i - 1][j + 1])
xpath.push_back(0);
else
xpath.push_back(1);
}
else if (j == image.w - 1) {
if (M[i - 1][j - 1] < M[i - 1][j])
xpath.push_back(-1);
else
xpath.push_back(0);
}
else {
if (M[i - 1][j - 1] <= M[i - 1][j] && M[i - 1][j - 1] <= M[i - 1][j + 1])
xpath.push_back(-1);
else if (M[i - 1][j] <= M[i - 1][j - 1] && M[i - 1][j] <= M[i - 1][j + 1])
xpath.push_back(0);
else if (M[i - 1][j + 1] <= M[i - 1][j - 1] && M[i - 1][j + 1] <= M[i - 1][j])
xpath.push_back(1);
}
}
path.push_back(xpath);
}
return path;
}
M M M中最后一行中的最小值,指示了最佳接缝路径的入口坐标。
Vec2i FindEntry(Image image, vector<vector<double>> M) {
vector<double> lastM;
for (int i = 0; i < image.w; i++) {
double m = M[image.h - 1][i];
lastM.push_back(m);
}
int minPosition = min_element(lastM.begin(), lastM.end()) - lastM.begin();
int x = image.h - 1;
int y = minPosition;
Vec2i p(x, y);
return p;
}
为了便于回溯,我们需要记录这条最佳接缝路径所经过的像素点坐标。
vector<Vec2i> FindTrackPath(vector<vector<int>> path, Vec2i p) {
vector<Vec2i> TrackPath;
TrackPath.push_back(p);
int x = p[0], y = p[1];
for (int i = x; i > 0; i--) {
if (path[i][y] == -1)
y -= 1;
else if (path[i][y] == 0)
;
else if (path[i][y] == 1)
y += 1;
Vec2i p(i - 1, y);
TrackPath.push_back(p);
}
return TrackPath;
}
3.删除接缝路径
对于图像缩小,我们可以直接在图像中删除这一条最佳接缝路径。
Image DeletePath(Image image, vector<Vec2i>BestTrackPath) {
for (int k = 0; k < BestTrackPath.size(); k++) {
int x = BestTrackPath[k][0];
int y = BestTrackPath[k][1];
image.colors[x].erase(image.colors[x].begin() + y);
}
image.w--;
return image;
}
4.复制接缝路径集合
对于图像增大,我们需要考虑更多。直接复制最佳接缝路径然后重复此过程是不可行的,这样会导致如下图所示的拉影效果,因为计算得到的最佳接缝路径每次都是最初的那条最佳接缝路径。

这里可以将图像增大中求最佳接缝路径问题转化为图像减小中求最佳接缝路径的问题。将初始图像复制到一个临时图像中,当求得一条最佳接缝路径时,在临时图像中删除这一条接缝而在初始图像中复制这一条接缝。
在具体的实现中,并不是每一次删除一条路径,而是将路径存储到集合中,路径上坐标所对应的像素值也存储到集合中,最后根据路径坐标集合中 y y y坐标递减的顺序在初始图像中插入像素点。
vector<Vec2i> GetCopyOrder(Image image, vector<vector<Vec2i>> yBestTrackPaths, int c) {
vector<int> yOfPath;
vector<Vec2i> copyorder;
for (int i = 0; i < c; i++)
for (int j = 0; j < image.h; j++) {
int y = yBestTrackPaths[i][j][1];
yOfPath.push_back(y);
}
for (int i = 0; i < yOfPath.size(); i++) {
int maxPosition = max_element(yOfPath.begin(), yOfPath.end()) - yOfPath.begin();
int x = maxPosition / image.h;
int y = maxPosition % image.h;
Vec2i b(x, y);
copyorder.push_back(b);
yOfPath[maxPosition] = -1;
}
return copyorder;
}
Image CopyPath(Image image, vector<Vec2i> copyorder, vector<vector<Vec2i>> BestTrackPaths) {
for (int i = 0; i < copyorder.size(); i++) {
int c_x = copyorder[i][0];
int c_y = copyorder[i][1];
int x = BestTrackPaths[c_x][c_y][0];
int y = BestTrackPaths[c_x][c_y][1];
image.colors[x].insert(image.colors[x].begin() + y + 1,image.colors[x][y]);
}
image.w = w;
return image;
}
三、具体功能
1.图像横向缩小
int r = abs(original_img.h - h);
int c = abs(original_img.w - w);
for (int i = 0; i < c; i++) {
vector<vector<double>>energy;
vector <vector<double>> M;
Vec2i entry;
vector<vector<int>> path;
vector<Vec2i> yBestPath;
energy = GetEnergy(original_img);
M = GetCost(original_img, energy);
entry = FindEntry(original_img, M);
path = FindPath(original_img, M);
yBestPath = FindTrackPath(path, entry);
DeletePath(original_img, yBestPath);
}
2.图像横向放大
int r = abs(original_img.h - h);
int c = abs(original_img.w - w);
Image tmp_img(original_img.h, original_img.w, 3);
for (int i = 0; i < original_img.h; i++)
for (int j = 0; j < original_img.w; j++)
tmp_img.colors[i][j] = original_img.colors[i][j];
vector<vector<Vec2i>> original_pos;
for (int i = 0; i < original_img.h; i++) {
vector<Vec2i> pos;
for (int j = 0; j < original_img.w; j++) {
Vec2i a(i, j);
pos.push_back(a);
}
original_pos.push_back(pos);
pos.clear();
}
vector<vector<double>>energy;
vector <vector<double>> M;
Vec2i entry;
vector<vector<int>> path;
vector<Vec2i> yBestPath;
vector<Vec2i> trackpath_pos;
vector<vector<Vec2i>> yBestTrackPaths;
vector<Vec2i> copyorder;
for (int i = 0; i < c; i++) {
energy = GetEnergy(tmp_img);
M = GetCost(tmp_img, energy);
entry = FindEntry(tmp_img, M);
path = FindPath(tmp_img, M);
yBestPath = FindTrackPath(path, entry);
for (int k = 0; k < yBestPath.size(); k++) {
int x = yBestPath[k][0];
int y = yBestPath[k][1];
trackpath_pos.push_back(original_pos[x][y]);
}
yBestTrackPaths.push_back(trackpath_pos);
for (int k = 0; k < yBestPath.size(); k++) {
int x = yBestPath[k][0];
int y = yBestPath[k][1];
original_pos[x].erase(original_pos[x].begin() + y);
}
trackpath_pos.clear();
tmp_img = DeletePath(tmp_img, yBestPath);
}
copyorder = GetCopyOrder(original_img, yBestTrackPaths, c);
CopyPath(original_img, copyorder, yBestTrackPaths);
3.图像纵向缩小
图像纵向变化可以通过将图像转置转化为图像的横向变化。
int r = abs(original_img.h - h);
int c = abs(original_img.w - w);
//转置图像
Image trans_img(original_img.w, original_img.h, 3);
for (int k = 0; k < original_img.w; k++)
for (int j = 0; j < original_img.h; j++)
trans_img.colors[k][j] = original_img.colors[j][k];
for (int i = 0; i < r; i++) {
vector<vector<double>>energy;
vector <vector<double>> M;
Vec2i entry;
vector<vector<int>> path;
vector<Vec2i> xBestPath;
energy = GetEnergy(trans_img);
M = GetCost(trans_img, energy);
entry = FindEntry(trans_img, M);
path = FindPath(trans_img, M);
xBestPath = FindTrackPath(path, entry);
trans_img = DeletePath(trans_img, xBestPath);
}
//将图像转置回来
original_img.colors.resize(trans_img.w);
for (int i = 0; i < trans_img.w; i++) {
original_img.colors[i].resize(trans_img.h);
for (int j = 0; j < trans_img.h; j++)
original_img.colors[i][j] = trans_img.colors[j][i];
4.图像纵向放大
int r = abs(original_img.h - h);
int c = abs(original_img.w - w);
//转置图像
Image trans_img(original_img.w, original_img.h, 3);
for (int k = 0; k < original_img.w; k++)
for (int j = 0; j < original_img.h; j++)
trans_img.colors[k][j] = original_img.colors[j][k];
Image tmp_img(trans_img.h, trans_img.w, 3);
vector<vector<Vec2i>> trans_pos;
vector<vector<double>>energy;
vector <vector<double>> M;
Vec2i entry;
vector<vector<int>> path;
vector<Vec2i> xBestPath;
vector<Vec2i> trackpath_pos;
vector<vector<Vec2i>> xBestTrackPaths;
vector<Vec2i> copyorder;
for (int i = 0; i < trans_img.h; i++)
for (int j = 0; j < trans_img.w; j++)
tmp_img.colors[i][j] = trans_img.colors[i][j];
for (int i = 0; i < trans_img.h; i++) {
vector<Vec2i> pos;
for (int j = 0; j < trans_img.w; j++) {
Vec2i a(i, j);
pos.push_back(a);
}
trans_pos.push_back(pos);
pos.clear();
}
for (int i = 0; i < r; i++) {
energy = GetEnergy(tmp_img);
M = GetCost(tmp_img, energy);
entry = FindEntry(tmp_img, M);
path = FindPath(tmp_img, M);
xBestPath = FindTrackPath(path, entry);
for (int k = 0; k < xBestPath.size(); k++) {
int x = xBestPath[k][0];
int y = xBestPath[k][1];
trackpath_pos.push_back(trans_pos[x][y]);
}
xBestTrackPaths.push_back(trackpath_pos);
for (int k = 0; k < xBestPath.size(); k++) {
int x = xBestPath[k][0];
int y = xBestPath[k][1];
trans_pos[x].erase(trans_pos[x].begin() + y);
}
trackpath_pos.clear();
tmp_img = DeletePath(tmp_img, xBestPath);
}
copyorder = GetCopyOrder(trans_img, xBestTrackPaths, r);
trans_img=CopyPath(trans_img, copyorder, xBestTrackPaths);
//将图像转置回来
original_img.colors.resize(trans_img.w);
for (int i = 0; i < trans_img.w; i++) {
original_img.colors[i].resize(trans_img.h);
for (int j = 0; j < trans_img.h; j++)
original_img.colors[i][j] = trans_img.colors[j][i];
}
original_img.h = h;
三、最终效果
1.图像横向放大
2.图像横向缩小
3.图像纵向缩小
4.图像纵向放大
5.图像横向放大、纵向缩小
四、总结
- 插入接缝路径时,要考虑坐标转换问题,因为像素点插入后其他像素点的坐标会改变。




