机器学习-随机森林算法

前言

在机器学习中，随机森林是一个包含多个决策树的分类器， 并且其输出的类别是由个别树输出的类别的众数而定。其实从直观角度来解释，每棵决策树都是一个分类器（假设现在针对的是分类问题），那么对于一个输入样本，N棵树会有N个分类结果。而随机森林集成了所有的分类投票结果，将投票次数最多的类别指定为最终的输出，这就是一种最简单的 Bagging 思想。

集成算法（Ensemble learning）：顾名思义就是集合了多种算法的结果从而使模型的预测效果表现地更好（以量取胜，基本上都是使用树模型）

集成学习的核心

如何产生“好而不同”的个体学习器，并准确性和多样性上做出最好的选择，正是集成学习的核心

假设现在用5个个体学习器做集成，最终结果用投票法产生，即少数服从多数。当个体学习器差异性不足的话，考虑一个极端例子，5个个体学习器都是由同一个学习器，复制而来，那么，5个学习器的预测结果和一个学习器预测结果完全相同，就达不到集成学习的目的了。因此，个体学习器应该“好而不同”，既要保证个体学习器的“准确性”，还要保证不同学习器之间的“多样性”。然而，准确性和多样性是冲突，在准确性和多样性上如何选择，才是集成学习需要解决的问题。

那么涉及到多棵树（多种算法），自然也就有了多种不同的使用方式，结合初中物理的电路知识，对比电阻的放置情况，就有了串联和并联和串并联等。集成算法模型目前常用的三种分别是Bagging、Boosting、Stacking，将其和电路进行类比方便我们理解，如下表

一、随机森林算法原理

首先是Bagging模型，其全称为：bootstrap aggregation，说大白话就是并行（并行：就是各玩各的，互不影响）训练了一堆分类器，其中最典型的代表就是随机森林。

关于随机森林的认识，单从字面上的意思进行理解即可，分为两块。

一个是随机，即是数据采样随机，特征选择随机；
一个是森林，即是把很多很多的决策树并行放在一起；

最后进行计算，如果是 分类 任务就是实行 众数取值 ，如果是 回归 就是进行 平均取值 ，以三棵树为例，对应如下


关于随机森林的理解，首先理解一下森林，就是将多个决策树进行组合放在一起，这个是没有太大的问题，那么为啥要随机呢？不随机会有什么现象呢，这里就假设用了100个树创建模型，输入的都是同一个数据，特征也选择的一样，那么经过训练后自然对应每一棵树中的节点都是相同的，最后分类或者回归的结果都是一致的，那么在计算最后的结果时候还是和一棵树的结果是一样的，也就没有必要再进行100棵树的组合了。

所以就有了随机的要求，为了尽可能的保证模型的效果好，采用的是随机数据样本和随机特征，这里假设有100条数据，每次创建一棵树都随机取80%的数据，然后在每个数据中取60%的特征，这样进行训练模型，必然最后的结果会有所不同，也就可以实现数据的分类与回归，图解如下：（为了绘图方便，这里以创建2个树为例），由于存在着两重随机性，基本上可以使得每棵树都不会一样，最终的结果也就会不一样

决策树的数量问题：是不是给的树越多，最后的模型效果越好呢？下图是创建模型后使用不同树的数量进行绘制的图形

理论上越多的树效果会越好，由上图中可以看出，实际上基本超过一定数量就差不多上下浮动了，树越多模型运行的时间越长，然而模型的效果也不是一定会很好，因此为了合理的选择决策树的数量，只能说差不多就行了。

二、随机森林的优势与特征重要性指标

2.1随机森林的优势

• 能够处理很高维度(feature很多)的数据，并且不用做特征选择
• 在训练完后，能够给出那些feature比较重要
• 容易做成并行化方法，速度比较快
• 可以进行可视化展示，便于分析

2.2特征重要性指标

首先举个例子，一组数据中有ABCD，其中A代表age年龄特征，模型训练完之后就想知道A特征有多重要。那么怎么评估 A的重要性？

首先是假设A中有五条数据分别为：21，23，25，37，46，51，那么第一次建立模型运行，计算错误率假设为err1 ,要看一个特征重要的程度。之后破坏(改变数据顺序或者加入噪音)A中的特征(比如开除一个员工，是否给公司带来的损失变大了，如果变大了，就说明A的重要性。如果没有太大变化，该员工可有可无，则该员工不重要，A的特征也不重要)。

然后就是随机森林采用的是树模型，其中节点的选择就是按照特征分类的重要性来设置的，因此通过每次分裂的节点就可以知道哪些特征比较重要，在训练模型完成之后也可以绘制特征重要性的条状图，方便可视化展示，这里给出的图示，后面会有代码实现。

三、提升算法概述

还是以一个例子开始入手，假设预测用户花费label：1000，那么使用随机森林模型，假定给出三棵树，分别得到的结果为1110,900,1200，最后随机森林预测的结果就为（1100+1200+900）/3 = 1100，对比电路模型，就是属于并联，取多个树的结果然后再计算均值（这个例子是回归任务）

那么使用提升算法Boosting该如何实现呢？，还是对比电路模型，它是首先有第一棵树，如果不行的话再加第二棵树，依次往后。比如首先创建第一棵树，预测的值为950，那么创建的第二棵树就要将之前的预测结果进行加强，也就是提升，所以针对的是第一棵树还有多少没有完成的量（弥补残差）进行预测，这里就是预测剩余的50，假使第二棵树预测值为30，然后就是将第一棵树和第二棵树看做一个整体，那么第三棵树的预测就是50-30=20，弥补前面所有的残差，假使第三棵树预测值为18，故最终的预测结果就是998


结合Boosting算法的公式理解：前面红色框的就是前一轮的预测结果，后面蓝色的是当前这一轮的，但是这一轮预测值往里加是有一个前提的，要求加进来的树是要让模型比原来的强为准，体现在损失上就是加入这棵树后损失是下降的。

典型代表有：AdaBoost， Xgboost

其中的 Xgboost 就可以通过上面那个998的案例进行理解，而 AdaBoost 会根据前一次的分类效果调整数据权重，如果某一个数据在这次分错了，那么在下一次我就会给它更大的权重，最终每个分类器根据自身的准确性来确定各自的权重，再合体，完成结果，如下，后面也会详细的通过代码进行介绍

四、Stacking堆叠模型

Stacking模型，就是进行堆叠，很暴力，拿来一堆直接上（各种分类器都来了），对比串并联电路，可以有不止一个串联电阻和并联电阻，反正套上就行（叠各种各样的分类器KNN,SVM,RF等等），为了刷结果，不择手段，多用于比赛刷分中，堆叠在一起确实能使得准确率提升，但是速度是个问题

特征：分阶段进行，举个例子（使用线性回归LR,决策树DT,随机森林RF进行堆叠），使用三个分类器进行三分类任务，进入第一阶段分别使用三个分类器进行预测，结果为[1,0,0]，[1,0,0]，[0,1,0]，那么接下来不是直接取这个预测结果的众数或者均值，而是将第一阶段的预测结果作为输入，然后选择分类器进入第二阶段（假设选择的是LR），图示如下

五、硬投票和软投票

1.1概念介绍

硬投票：就是只拿最后的结果就事论事，如下，一组数据经过各个预测器后给出的结果分别是1,1,2,1，那么最后的预测结果就是1（少数服从多数）

软投票：就是考虑到各个分类器中的概率值进行加权平均。最终看的是概率值

1.2硬投票展示

import warnings
warnings.filterwarnings('ignore')
import numpy as np
import os 
import matplotlib.pyplot as plt

from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split

#集成学习，这里可以把数据量调大一下，比如选择500个数据量，设定一些噪声
X,y = make_moons(n_samples = 500, noise = 0.30, random_state = 42)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 42)

#然后分别选取标签为0和1的数据进行绘图展示
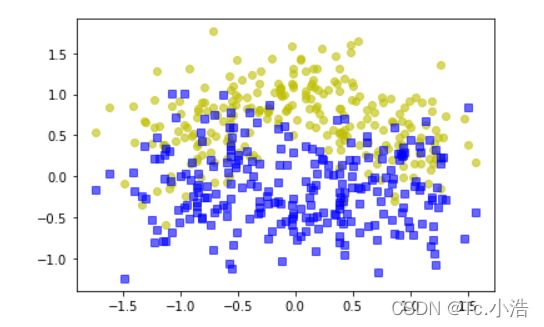
plt.plot(X[:,0][y==0],X[:,1][y==0],'yo')
plt.plot(X[:,0][y==0],X[:,1][y==1],'bs')

1.3硬投票和软投票效果对比

投票策略：软投票与硬投票

• 硬投票：直接用类别值，少数服从多数
• 软投票：各自分类器的概率值进行加权平均

硬投票：

数据的获取参考上面的代码

from sklearn.ensemble import RandomForestClassifier,VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC

#创建多个分类器的实例
log_clf = LogisticRegression()
rnd_clf = RandomForestClassifier()
svm_clf = SVC() #支持向量机在之后的博客中会更新，这里拿来用一下

#构建投票分类器
voting_clf = VotingClassifier(estimators = [('lr',log_clf),('rf',rnd_clf),('svc',svm_clf)],voting = 'hard')

#训练模型，可以只是看投票分类器的结果
#voting_clf.fit(X_train,y_train)

#也可以查看所有分类器的结果，进行遍历循环然后进行输出结果即可
from sklearn.metrics import accuracy_score
for clf in (log_clf,rnd_clf,svm_clf,voting_clf):
    clf.fit(X_train,y_train)
    y_pred = clf.predict(X_test)
    print(clf.__class__.__name__,accuracy_score(y_test,y_pred))
#结果
LogisticRegression 0.864
RandomForestClassifier 0.904
SVC 0.896
VotingClassifier 0.904

软投票

接下来就是进行软投票的代码实现，需要该改动的就是voting=‘soft’,另外由于软投票针对的是概率值，SVC分类器中的参数probability默认是False，因此需要设置为True

from sklearn.ensemble import RandomForestClassifier,VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC

#创建多个分类器的实例,
log_clf = LogisticRegression(random_state = 42)
rnd_clf = RandomForestClassifier(random_state = 42)
svm_clf = SVC(probability=True,random_state = 42) #支持向量机，使用概率

#构建投票分类器,传入三个分类器
voting_clf = VotingClassifier(estimators = [('lr',log_clf),('rf',rnd_clf),('svc',svm_clf)],voting = 'soft')
from sklearn.metrics import accuracy_score
for clf in (log_clf,rnd_clf,svm_clf,voting_clf):
    clf.fit(X_train,y_train)
    y_pred = clf.predict(X_test)
    print(clf.__class__.__name__,accuracy_score(y_test,y_pred))

#结果
LogisticRegression 0.864
RandomForestClassifier 0.896
SVC 0.896
VotingClassifier 0.92

软投票会比硬投票好一点

六、Bagging策略

Bagging策略

• 首先对训练数据集进行多次采样，保证每次得到的采样数据都是不同的
• 分别训练多个模型，例如树模型
• 预测时需得到所有模型结果再进行集成
  
  实验代码

from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier

bag_clf=BaggingClassifier(
    #使用树模型
    DecisionTreeClassifier(),
    #使用500个树
    n_estimators=500,
    #样本数
    max_samples=100,
    #又放回的
    bootstrap=True,
    random_state=42
)
#传入数据进行训练
bag_clf.fit(X_train,y_train)
#使用测试集进行测试
y_pred=bag_clf.predict(X_test)
#得到测试结果
accuracy_score(y_test,y_pred)
0.904

单独使用树模型

tree_clf=DecisionTreeClassifier(random_state=42)
tree_clf.fit(X_train,y_train)
y_pred_tree=tree_clf.predict(X_test)
accuracy_score(y_test,y_pred_tree)
 0.856

可以得出使用Bagging策略比单独使用树模型得到是结果要好

决策边界展示

比如查看一下集成与传统方法的对比，关于绘制决策边界的代码，封装成函数，这里就不再详述了，可以网上找到很多，直接修改里面一些参数即可出图

from matplotlib.colors import ListedColormap #这里导入颜色包

#axes参数的取值根据上面绘制的图像的x,y轴的取值范围确定，然后默认绘制等高线
def plot_decision_boundary(clf,X,y,axes=[-2,2,-1.5,2],alpha=0.5,contour=True):  
    x1s = np.linspace(axes[0],axes[1],100)
    x2s = np.linspace(axes[2],axes[3],100)
    x1,x2 = np.meshgrid(x1s,x2s)
    X_new = np.c_[x1.ravel(),x2.ravel()]
    y_pred = clf.predict(X_new).reshape(x1.shape)
    custom_cmp = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
    plt.contourf(x1,x2,y_pred,cmap = custom_cmp,alpha = 0.8)
    if contour:
        custom_cmp2 = ListedColormap(['#7d7d58','#4c4c7f','#507d50'])
        plt.contour(x1,x2,y_pred,cmap = custom_cmp2,alpha = 0.8)
    plt.plot(X[:,0][y==0],X[:,1][y==0],'yo',alpha=0.6)
    plt.plot(X[:,0][y==0],X[:,1][y==1],'bs',alpha=0.6)
    plt.axis(axes)
    plt.xlabel('x1')
    plt.ylabel('x2')

#创建画布，分别创建两个子图进行展示
plt.figure(figsize=(12,5))
plt.subplot(121)
plot_decision_boundary(tree_clf,X,y)
plt.title('decide tree')
plt.subplot(122)
plot_decision_boundary(bag_clf,X,y)
plt.title('decide tree with bagging')

输出的结果为：（可以看出经过bagging策略后决策的边界要比普通的决策树要平滑的多，也可以看到在左侧的一些数据边界是直接垂下来了，这部分数据分开的难度太大了，都几乎融合在一块了，所以最后模型只能是尽量的进行划分多的数据）

八、OOB袋外数据的作用

OOB策略：Out Of Bug，这个外是针对于bagging这个袋子而言的，bagging采取的随机抽样的方式去建立树模型（可以参考一下随机森林算法原理的图示），那么那些未被抽取到的样本集，也就是未参与建立树模型的数据集就是袋外数据集，我们就可以用这部分数据集去验证模型效果，默认值为False，如果改变为True，就可以直接使用这部分数据进行检测模型的可靠性，就不用再额外的做一些交叉验证的操作了

from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
bag_clf_OOB = BaggingClassifier(
    DecisionTreeClassifier(), 
    n_estimators=500, 
    max_samples=100,
    bootstrap=True,
    random_state = 42,
    oob_score=True #其余的都不变，添加该参数
)
bag_clf_OOB.fit(X_train,y_train)
bag_clf_OOB.oob_score_ 
#模型训练后，有oob_score_ 方法用来评估模型的得分

输出的结果为：0.9253333333333333

而如果采用sklearn中封装好的accuracy_score方法进行评估，代码如下：

y_pred = bag_clf.predict(X_test)
accuracy_score(y_test,y_pred)
#输出结果为：0.904  比采用oob的数据评价的要低

九、特征重要性可视化展示

关于特征重要性前面已经提及到，可以通过打乱或者破坏某个特征从而查看某个特征的重要性，在集成学习中使用的几乎都是树模型，本身节点就代表着重要程度的大小，那么具体要量化判断的话，在sklearn中是看每个特征的平均深度，也就是节点越往上，那么这个特征就越重要，反之就越不重要。这里的数据首先使用鸢尾花数据集（数据较少，特征也简单），看一下输出的特征重要性是什么样的，代码如下

from sklearn.datasets import load_iris
iris = load_iris()
rf_clf = RandomForestClassifier(n_estimators=500,n_jobs=-1)
rf_clf.fit(iris['data'],iris['target'])
for name,score in zip(iris['feature_names'],rf_clf.feature_importances_):
    print (name,score)
    plt.barh(name,score)

输出的结果为：（后面的数值就代表这平均深度的取值，说明花瓣的长度和宽度对模型的分类很重要）

十、AdaBoost算法决策边界展示

前面简单的提到了AdaBoost算法，类别于串联电路，功能是一步步进行累加的。举个例子进行理解，就是初高中时候做题或者考试的时候，会有一个错题本，每次将里面的难题或者易错的题收集起来，多看多练习，下次在遇到的时候就不会做错了。Adaboost算法就是一样的道理，在创建每一个模型的时候就会想一想上一次训练的时候哪一些样本没有做好，那么这次就得额外重视一下还没有做好的样本数据。

在AdaBoost中有一个 样本的权重项 ，因此之后在往模型中输入数据的时候就不会都是同样的权重了，如下图示，最初的时候是相同的权重，模型训练后出现问题后，进行权重的调整，如果还出现问题，继续进行权重的调整（没有问题的数据权重调的小一些，有问题的数据权重调的大一些），这样每次调整之后就会有一个准确率，最后的结果就是加权平均，假如下图的上面三个结果（ABC）分别有90%、80%、50%的准确度，那么最终的结果就是0.9A+0.8B+0.5C。

以SVM分类器为例来演示AdaBoost的基本策略（这里就是展示AdaBoost是怎么一步步实现的）

from sklearn.svm import SVC #重新导入一下，这里先用一下，后面更新的博文会详细介绍

m = len(X_train) #计算数据的长度

plt.figure(figsize=(14,5))
#创建两个子图， 不同的学习率
for subplot,learning_rate in ((121,1),(122,0.5)):
    sample_weights = np.ones(m)#设置的初始权重都为1
    plt.subplot(subplot) 
    #进行五次结果权重的调整
    for i in range(5):
        svm_clf = SVC(kernel='rbf',C=0.05,random_state=42) #创建模型
        svm_clf.fit(X_train,y_train,sample_weight = sample_weights) #训练模型
        y_pred = svm_clf.predict(X_train)#然后计算预测值
        sample_weights[y_pred != y_train] *= (1+learning_rate) #根据预测值和真实值的差值进行权重的调整
        plot_decision_boundary(svm_clf,X,y,alpha=0.2)#显示每次调整的边界
    plt.title('learning_rate = {}'.format(learning_rate))#打印标题
    #这里就是对决策边界标一下号
    if subplot == 121:
        plt.text(-0.7, -0.65, "1", fontsize=14)
        plt.text(-0.6, -0.10, "2", fontsize=14)
        plt.text(-0.5,  0.10, "3", fontsize=14)
        plt.text(-0.4,  0.55, "4", fontsize=14)
        plt.text(-0.3,  0.90, "5", fontsize=14)
plt.show()

输出结果为：（最后的标记数值，就可以显示AdaBoost每次调整的结果，以上代码是属于手写代码进行AdaBoost的基本策略的演示，实际上可以直接使用sklearn封装好的模块进行模型创建）

from sklearn.ensemble import AdaBoostClassifier
ada_clf = AdaBoostClassifier(DecisionTreeClassifier(max_depth=1), #为了更好的展示最后的分界，这里设置树的深度为1
                   n_estimators = 200,
                   learning_rate = 0.5,
                   random_state = 42
)

ada_clf.fit(X_train,y_train)
plot_decision_boundary(ada_clf,X,y)

输出的结果为：（直接将最终的结果展示出来）

十一、Gradient Boosting梯度提升算法

也就是之前举得998示例，基于此算法共有三个版本，最初的GBDT,后来发展到了XGBoost和最新的LightGBM,这里就介绍一下最初的GBDT提升算法的基本流程，后面两个算法也是基于同一原理，会 在之后的实际案例中会进行展示。

首先指定一下数据，然后就是依次传入数据，创建模型并训练模型，最后是进行整体模型的预测

np.random.seed(42)
X = np.random.rand(100,1) - 0.5 #X变量是列表嵌套的
y = 3*X[:,0]**2 + 0.05*np.random.randn(100)

#创建回归树模型
from sklearn.tree import DecisionTreeRegressor
#开始创建第一个树并进行训练
tree_reg1 = DecisionTreeRegressor(max_depth = 2)
tree_reg1.fit(X,y)

#然后使用残差进行第二棵树的创建和训练
y2 = y - tree_reg1.predict(X)
tree_reg2 = DecisionTreeRegressor(max_depth = 2)
tree_reg2.fit(X,y2)

#同理进行第三棵树的创建和训练
y3 = y2 - tree_reg2.predict(X)
tree_reg3 = DecisionTreeRegressor(max_depth = 2)
tree_reg3.fit(X,y3)

#最后计算预测的结果，即为所有模型结果之和
X_new = np.array([[0.8]]) #假使预测数据x为0.8
y_pred = sum(tree.predict(X_new) for tree in (tree_reg1,tree_reg2,tree_reg3))
y_pred

输出结果为：array([0.75026781])