《PyTorch深度学习实践》学习笔记(1)

一 线性回归模型（有监督学习）

回归问题：如果我们预测的结果是以连续数字进行表示，即我们将在连续函数中对多个输入变量建立映射关系时，则这样的问题称之为回归问题

1 线性模型

$$y=\omega x+b$$

2 损失函数

误差函数

$$loss=(y-y{)}^2=(x\ast \omega -y{)}^2$$

平均平方误差(MSE)

$$cost=\frac{1}{N}\sum _{n=1}^N(y_n-y_n{)}^2$$

3 代码详解

import numpy as np
import matplotlib.pyplot as plt;

x_data = [1.0, 2.0, 3.0]        //测试集数据
y_data = [2.0, 4.0, 6.0]

#线性模型
def forward(x):                 //前馈计算y值
   return x * w
                               
#损失函数                       、
def loss(x, y):                 // 损失函数
   y_pred = forward(x)
   return (y_pred - y) * (y_pred - y)  

#迭代取值，计算每个w取值下的x，y，y_pred,loss_val
w_list = []
mse_list = []
for w in np.arange(0.0, 4.1, 0.1):
   print('w=', w)
   l_sum = 0
   for x_val, y_val in zip(x_data, y_data):
       y_pred_val = forward(x_val)
       loss_val = loss(x_val, y_val)
       l_sum += loss_val
       print('\t', x_val, y_val, y_pred_val, loss_val)
   print('MSE=', l_sum / 3)
   w_list.append(w)
   mse_list.append(l_sum / 3)

##画图
plt.plot(w_list, mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()

训练结果

4 用Pytorch实现线性回归

(1) 准备数据

import torch
//注意x,y必须为矩阵
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[2.0], [4.0], [6.0]])

(2) 使用Class设计模型，类继承于 nn.Module

实例化模型

import torch
class LinearModel(torch.nn.Module):
//必须包含__init__()和forward()两个函数，Module自动生成Backward()    
    def __init__(self):          
         super(LinearModel, self).__init__()
         self.linear = torch.nn.Linear(1, 1)
// 这里的nn.Linear类包含了两类Tensors:Weight和bias
    def forward(self, x):
         y_pred = self.linear(x)
         return y_pred        
model = LinearModel()

(3) 构建损失函数和优化器 using Pytorch API

criterion = torch.nn.MSELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)   
//parameters为模型内全部参数(w,b),lr为学习率

其中这里采用的优化器是SGD(随机梯度下降)，损失函数为MSELoss
常见的优化器还有：
• torch.optim.Adagrad
• torch.optim.Adam
• torch.optim.Adamax
• torch.optim.ASGD
• torch.optim.LBFGS
• torch.optim.RMSprop
• torch.optim.Rprop
• torch.optim.SGD

(4) 训练 forward, backward, update

for epoch in range(1000):
     y_pred = model(x_data)
     loss = criterion(y_pred, y_data)
     print(epoch, loss.item())
     optimizer.zero_grad()   #清零，因为grad会累加
     loss.backward()         #Auto Grad
     optimizer.step()        #update    

(5) 最终完整代码

import torch
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[2.0], [4.0], [6.0]])
#实例化模型
class LinearModel(torch.nn.Module):
		def __init__(self):
			super(LinearModel, self).__init__()
			self.linear = torch.nn.Linear(1, 1)
		def forward(self, x):
			y_pred = self.linear(x)
			return y_pred
model = LinearModel()

criterion = torch.nn.MSELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

for epoch in range(1000):
		y_pred = model(x_data)
		loss = criterion(y_pred, y_data)
		print(epoch, loss.item())
		optimizer.zero_grad()      #清零，因为grad会累加
		loss.backward()            #Auto Grad
		optimizer.step()           #update
		
#Output weight and bias
print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())
# Test Model
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ', y_test.data)

训练结果如下：

二 分类问题模型（Logistic）（有监督学习）

分类问题：如果我们预测的结果是以离散形式表示的，即我们将多个输入变量与多个不同类别建立映射关系时，则这样的问题称之为分类问题。

1 二分类问题

2.1.1 sigmod函数层

sigmod函数表达式
$$\sigma (z)=\frac{1}{1+e^{-z}}$$
线性模型表达式：$$y=\omega \ast x+b$$
线性模型示意图

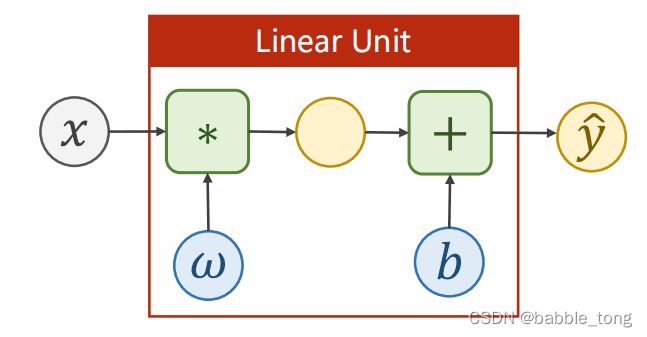
线性模型代码：
class LinearModel(torch.nn.Module):
	def __init__(self):
		super(LinearModel, self).__init__()
		self.linear = torch.nn.Linear(1, 1)
	def forward(self, x):
		y_pred = self.linear(x)
		return y_pred

回归模型表达式：$$y=\sigma (\omega \ast x+b)$$
$$y=\sigma (y)=\frac{1}{1+e^{-y}}$$
回归模型示意图

回归模型代码：
import torch.nn.functional as F
class LogisticRegressionModel(torch.nn.Module):
	def __init__(self):
		super(LogisticRegressionModel, self).__init__()
		self.linear = torch.nn.Linear(1, 1)
	def forward(self, x):
		y_pred = F.sigmoid(self.linear(x))  //仅这里不同
		return y_pred

2.1.2 损失函数

回归模型中常见损失函数

          KL散度    交叉熵（BCELoss）

交叉熵公式

$$loss=-\frac{1}{N}\sum _{n=1}^N{y}_{n}log{y}_n+(1-y_n)log(1-y_n)$$

交叉熵代码

criterion = torch.nn.BCELoss(size_average=False)

2.1.3 用Pytorch实现二分类回归完整代码

import torch
import torch.nn.functional as F
#数据集准备
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])
#实例化模型
#-------------------------------------------------------#
class LogisticRegressionModel(torch.nn.Module):
	def __init__(self):
		super(LogisticRegressionModel, self).__init__()
		self.linear = torch.nn.Linear(1, 1)
	def forward(self, x):
		y_pred = F.sigmoid(self.linear(x))
		return y_pred
model = LogisticRegressionModel()
#选择损失函数和优化器
criterion = torch.nn.BCELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
#训练
for epoch in range(1000):
	y_pred = model(x_data)
	loss = criterion(y_pred, y_data)
	print(epoch, loss.item())
	optimizer.zero_grad()
	loss.backward()  
	optimizer.step()    #for x,y in zip(x_data,y_data)
		                # w.data=w.data-0.01*w.grad.data
#可视化
'''
numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)
在指定的间隔内返回均匀间隔的数字。
返回num均匀分布的样本，在[start, stop]。
这个区间的端点可以任意的被排除在外。
'''	
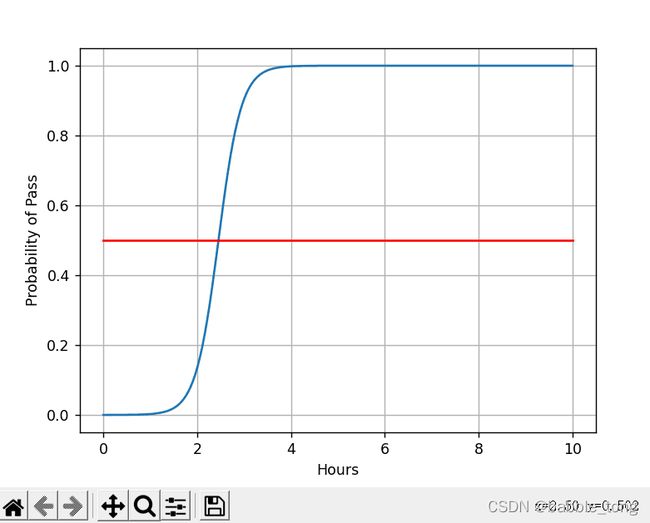
x = np.linspace(0, 10, 200)            #在0~10中，均匀取出200个点
x_t = torch.Tensor(x).view((200, 1))   #将200个点变成（200,1）的张量
y_t = model(x_t)                       #得到y_pred_t是个张量
y = y_t.data.numpy()                   #将y_pred_t张量转化为矩阵形式
# 绘图
plt.plot(x, y)
plt.plot([0, 10], [0.5, 0.5], c='r')
plt.xlabel('Hours')
plt.ylabel('Probability of Pass')
plt.grid()
plt.show()

训练结果

2 多分类问题

2.2.1 Softmax函数

需要在线性层后加一个Softmax层 （如下图所示，输出为10个类别）

Softmax计算过程
$$P(y=i)=\frac{e^{z_i}}{{\sum }_{j=0}^{K-1}{e}^{Z_j}},iϵ[0,...,K-1]$$
用输出三个类别来说明Softmax函数运算的过程图

注：
1）将每一个输出值Zi都采用指数幂的运算，保证结果都是正数；
2）分母是每个指数幂结果的求和，保证最后输出的K个结果的总和为1（本质就是归一化操作）

2.2.2 损失函数

NLLLoss() （Negative Log Likelihood Loss最大似然损失函数）

numpy实现代码

import numpy as np
y = np.array([1, 0, 0])
z = np.array([0.2, 0.1, -0.1])
y_pred = np.exp(z) / np.exp(z).sum()
loss = (- y * np.log(y_pred)).sum()
print(loss)

Pytorch实现代码

torch.nn.NLLLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')

模型图

EntropyLoss() (交叉熵损失函数)

Pytorch实现代码

import torch
criterion = torch.nn.CrossEntropyLoss()
y = torch.LongTensor([0])              #y是真实的标签值
z1 = torch.Tensor([[0.4, 0.1, 0.1]])   #z是交叉熵函数的输入
z2 = torch.Tensor([[0.1, 2.7, -0.1]])
loss1 = criterion(z1, y)
loss2 = criterion(z2, y)
print("Batch Loss1=",loss1.data,"Batch Loss2=",loss2.data)
#在pytorch中直接调用类函数实现，函数具体参数说明如下：
torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')

输出结果

可以看出交叉熵的基本性质
模型图

计算公式：
$$loss(x,class)=-log(\frac{exp(x[class])}{{\sum }_{j}exp(x[j])})=-x[class]+log(\sum _{j}exp(x[j]))$$
易错：在使用交叉熵损失函数时，在线性层最后不能做激活，因为其已经包含在交叉熵函数中

小结： CrossEntropy↔LogSoftMax+NLLLoss （交叉熵损失函数与NLL损失函数的关系如式所示）

2.2.3 多分类问题案例——MNIST手写数字分类

部分代码功能介绍

batch_size = 64                         #方便进行dataset和dataloader，进行批量化操作
transform = transforms.Compose([        #主要是图像方面的读入处理，Convert the PIL Image to Tensor
    transforms.ToTensor(),
    transforms.Normalize((0.1307),(0.3081))  #均值和标准差，对于该数据集来说是定值
])

     代码功能：神经网络在进行处理的时希望输入数值比较小，在-1到1之间同时遵从正态分布。所以要将输入图像的像素值0-255转变为图像张量，像素值为0-1之间

完整可运行代码

import torch
from torchvision import transforms          #主要针对图像进行处理  
from torchvision import  datasets
from torch.utils.data import DataLoader     #前三个包主要是构建DataLoader 
import torch.nn.functional as F             #For using function relu()/不用之前的sigmoid
import matplotlib.pyplot as plt             #For constructing Optimizer

#准备数据,转换成张量类型的数据，并进行归一化操作
batch_size = 64                         #方便进行dataset和dataloader，进行批量化操作
transform = transforms.Compose([        #主要是图像方面的读入处理，Convert the PIL Image to Tensor
    transforms.ToTensor(),              #convert a PIL(Python Image Library就是普通图片) image to tensor (H*W*C) in range [0,255] to a torch.Tensor(C*H*W) in the range [0.0,1.0]
    transforms.Normalize((0.1307),(0.3081)) #	用均值和标准差归一化张量图像
])                                          #   image=(image-mean)/std
train_dataset = datasets.MNIST(root = "../dataset/mnist",  
                               train = True,download=True,transform = transform)
                                            #一般大型数据都需要用dataset和dataload来进行操作
train_loader = DataLoader(train_dataset,shuffle = True,batch_size = batch_size)

test_dataset = datasets.MNIST(root = "../dataset/mnist",train = False,
                              download=True,transform = transform)
test_loader = DataLoader(test_dataset,shuffle = True,batch_size = batch_size)

#自定义多层模型
class Net(torch.nn.Module):
    def __init__(self):
        super(Net,self).__init__()                #总共需要5个线性层
        self.linear1 = torch.nn.Linear(784,512)   #因为输入图像 是N*1*28*28的经过Tonsor变成N*784
        self.linear2 = torch.nn.Linear(512,256)
        self.linear3 = torch.nn.Linear(256,128)
        self.linear4 = torch.nn.Linear(128,64)
        self.linear5 = torch.nn.Linear(64,10)

    def forward(self,x):            #使用ReuLU激活单元
        x = x.view(-1,784)          #view作用：改变张量的形状，变成二阶的张量(一个矩阵)，-1的的作用是输入图片后自动的求解有多少个像素，本次为784
        x = F.relu(self.linear1(x))
        x = F.relu(self.linear2(x))
        x = F.relu(self.linear3(x))
        x = F.relu(self.linear4(x))
        return self.linear5(x)      #最后一层线性层的结果直接输出，不再激活，后面要接Softmax
model = Net()

#构建损失函数的计算和优化器
criterion = torch.nn.CrossEntropyLoss()#多分类交叉熵损失函数
op = torch.optim.SGD(model.parameters(),lr = 0.01,mouentum=0.5)#采用SGD

#训练过程，包括前向计算和反向传播，封装成一个函数
def train(epoch):
    running_loss = 0.0
    for batch_idx,data in enumerate(train_loader,0):
        inputs,target = data   #inputw为x,traget为y
        op.zero_grad()         #优化器清零
        #前馈+反馈+更新
        #前向计算
        outputs = model(inputs)
        loss = criterion(outputs,target)
        #反向传播与权值更新
        loss.backward()
        op.step()

        running_loss += loss.item()  #取loss值时要用.item()
        if batch_idx % 300 == 299:#每训练300代就输出一次
            print('[%d,%5d] loss: %3f' % (epoch+1,batch_idx+1,running_loss / 300))
            running_loss = 0.0

#测试过程，封装成函数
def test():
    correct = 0
    total = 0
    with torch.no_grad():#因为test的过程无需反向传播，也就不需要计算梯度
        for data in test_loader:    #从test里取数据
            images,labels = data    
            outputs = model(images) #预测
            _,predicted = torch.max(outputs.data,dim = 1)#因为是按批给的数据所以得到的数据标签也是一个矩阵   #返回值：最大值，最大值的坐标值
            total += labels.size(0) #同样labels也是一个Nx1的张量
            correct += (predicted == labels).sum().item()  #张量之间的比较运算
        print('Accuracy on test set: %d %%'%(100 * correct / total))

#主函数逻辑
if __name__ == '__main__':
    for epoch in range(10): #Training cycle （因为针对大型数据来讲需要分批导入进行训练，及Mini-Batch）
        train(epoch)
        test()

训练结果