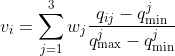数字孪生论文阅读笔记【1.2】
[1]刘劲松. 高档数控机床数字孪生关键技术研究与应用[D].中国科学院大学(中国科学院沈阳计算技术研究所),2022.DOI:10.27587/d.cnki.gksjs.2022.000005.
实验验证
故障诊断卷积神经网络
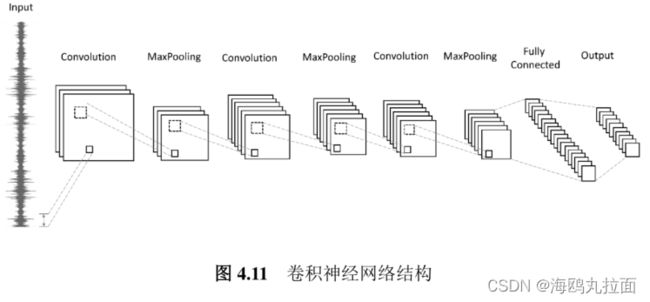
实验使用卷积神经网络结构如下图,包含三个卷积层,三个池化层,一个全连接隐含层,一个Softmax层。故障数据通过第一个卷积层以及ReLU激活函数,输出一组特征图(Feature Maps)再经过最大值池化进行降采样。重复两次以上操作,将最后一个池化层输出的特征图与全连接隐含层相连,经过ReLU函数激活后,传递到最后的Softmax层。
第一个卷积层卷积核数量为16,卷积核大小为62×1,步长为16×1;第二和第三个卷积层的卷积核数量为64,卷积核大小为3×1,步长为1×1。第一个池化层滑动窗口大小为2×1,步长为1×1 ;第二个和第三个池化层滑动窗口大小为2×1,步长为2×1。全连接层的神经元个数为64,经过Softmax层输出的类别个数为10。
故障知识图谱构建与验证
没接触过,没看懂......就看个意思吧┗( ▔, ▔ )┛
高档数控机床数字孪生生产重调度决策方法研究
Motivation
当检测到数控机床故障信息时,根据故障知识图谱检索推理得到该故障的维护知识,并以这些知识为约束条件,采用重调度决策算法辅助更新生产计划,为生产计划方案的动态调整与执行提供决策支持。针对高档数控机床数字孪生生产重调度决策问题,提出一种故障诊断和生产重调度集成决策体系结构,旨在实现智能的故障维护和生产重调度决策。
故障诊断和生产重调度集成决策体系结构
(1)故障诊断层。本层基于之前提出的数据感知方法构建高档数控机床全要素感知数据采集网络,实现对数控机床全要素感知数据的实时获取,映射数控机床实时运行状态数据到信息空间中,保持物理实体与数字孪生模型的一致,为数控机床的故障诊断提供丰富的信息。之前提出的故障诊断技术实现对数控机床故障的智能诊断。
(2)知识应用层。 基于构建的数控机床故障知识图谱,应用知识图谱检索和推理技术,实现故障的多层次分析,快速高效进行故障维护,知识传递与共享,同时也为智能决策层提供知识支撑。
(3)智能决策层。 在故障诊断层对故障做出诊断结果时,通过知识应用层提供的维护知识(如维护原因、维护措施、预计维护时间等),在智能决策层可以对数控机床故障维护提供指导,同时针对新的故障维护策略对原有维护知识进行更新。
重调度决策算法模型
采用以下符号建立重调度决策模型:
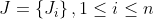 ,J表示n个已完成初始调度的作业。
,J表示n个已完成初始调度的作业。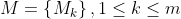 ,M表示m台机床。
,M表示m台机床。- 每个作业
 都有一组有序的任务序列,即
都有一组有序的任务序列,即 ,
,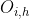 表示作业
表示作业 的第h个任务,
的第h个任务, 表示作业
表示作业 的任务总数。
的任务总数。 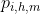 表示作业
表示作业 中的任务
中的任务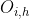 在机床
在机床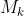 上加工所用的时间。
上加工所用的时间。
数字孪生驱动的生产重调度决策问题可以看做是一个约束调度问题,其主要目标是实现调度方案的高效以及原始调度方案的偏差最小化。因此考虑效率性能和稳定性两类重要性能指标,并采用能体现重调度决策方案效率的最大完工时间(表示为![]() )以及从不同方面表现重调度决策方案稳定性的起始时间偏差(表示为SI)与序列偏差(表示为F)三个指标进行重调度决策方案的性能评价,计算方式分别如下:
)以及从不同方面表现重调度决策方案稳定性的起始时间偏差(表示为SI)与序列偏差(表示为F)三个指标进行重调度决策方案的性能评价,计算方式分别如下:
算法框架
蒙特卡洛树搜索方法介绍参考:https://www.bilibili.com/video/BV1JD4y1Q7mV/?spm_id_from=333.337.search-card.all.click&vd_source=0ef0e3dcc699e4536466b007ec6c95cf
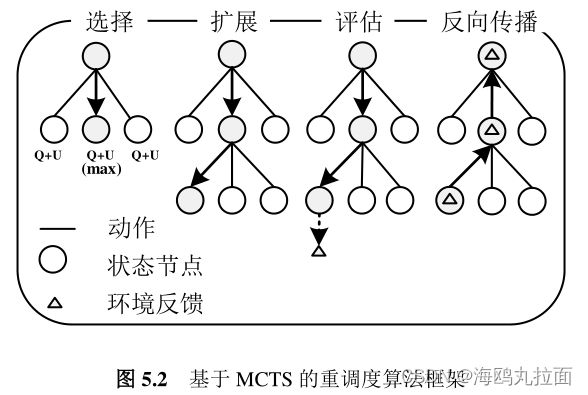
采用蒙特卡洛树搜索方法构造重调度决策算法,整体算法框架如下所示:
蒙特卡洛搜索树中的每一个状态节点表示当前调度的一个状态,状态节点分为终止节点与非终止节点两类,终止节点为全部任务调度完成状态,之后不再有行为,因此不包含任何边。非终止节点与终止节点相反,当前调度状态下还有未安排的任务,包含一组边(s,a)每条边对应当前状态s下的合法行为空间A(s)中的一个行为a,行为空间中的行为根据当前调度状态由调度规则组成,并且每条边中存储着统计数据:
![]()
其中N(s,a)是该边的访问次数,Q(s,a)为该边的全局行为价值,P(s,a)为该边的选择概率。在进行每个状态的搜索中,若节点不为终止状态节点,则算法构建一个以当前状态节点为根节点的搜索树,该树包含该状态下合法动作空间中的所有动作,并选择其中一个动作进行扩展,最终通过多次扩展构建一个完整的重调度序列,并对该重调度序列进行评估与反向传播,用于优化下一回合的搜索。因此该算法分为选择、扩展、评估和反向传播四个阶段,以下对四个阶段进行详细介绍。
选择阶段
当访问到的状态节点st为已探索的非终止节点时,对当前状态下合法行为空间中的行为进行选择。采用上限置信区间算法选择当前状态St的行为at:
其中![]() 为决定探索程度的常数。当访问到的状态节点st为未探索的非终止节点时,算法进入扩展阶段,对节点状态进行行为探索。
为决定探索程度的常数。当访问到的状态节点st为未探索的非终止节点时,算法进入扩展阶段,对节点状态进行行为探索。
扩展阶段
当st为未探索非终止节点时,进行拓展:
![]()
其中,Paj为当前状态节点下的合法行为空间为A(s)={a1,a2,...,an}时,行为ai的选择概率,Paj计算公式如下:
其中vi表示当前状态下执行行为ai得到状态节点的局部行为价值。综上,联合指标值(Unit Index Value,UIV)的计算方式如下:
其中w={w1,w2,w3}分别表示调度策略中Cmax、SI与F所占的用户偏好权重,且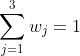 ,qi1、qi2与qi3分别表示执行行为ai后得到状态节点的Cmax、SI与F的值,
,qi1、qi2与qi3分别表示执行行为ai后得到状态节点的Cmax、SI与F的值,![]() 和
和![]() 分别表示所有行为得到的状态节点中指标j的最大值与最小值。
分别表示所有行为得到的状态节点中指标j的最大值与最小值。
评估阶段
若在本回合中当前访问的状态节点为终止状态节点,则进入评估阶段,评估阶段根据本回合得到调度序列的指标值,计算本回合的反馈值,用于在反向传播过程中更新路径上每个行为中的Q值。
反向传播阶段
反向传播用于实现评估价值的回溯,从而更新Q值。首先对所有搜索路径中经过的边的计数加1,即![]() ,并采用下式更新该边Q值:
,并采用下式更新该边Q值: