小瓜讲机器学习——聚类算法(三)DBSCAN算法原理及Python代码实现
文章目录
-
-
-
-
- 3. DBSCAN算法
-
- 3.1 样本点类别
- 3.2 直接密度可达、密度可达、密度连接
- 3.3 DBSCAN算法过程
- 3.4 DBSCAN算法Python代码实现
- 附录:Python源代码
-
- 文章导引列表:
- 机器学习
- 数据分析
- 数据可视化
-
-
-
3. DBSCAN算法
K-Means和Mean Shift聚类算法都是基于距离的聚类算法,均存在共同的局限性就是只能在凸集(见图1)上进行,在非凸集上面会导致错误的结果,比如图2中所示。

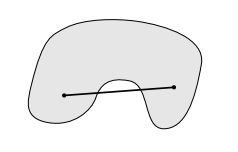
凸集合 非凸集合
图1 凸集和非凸集
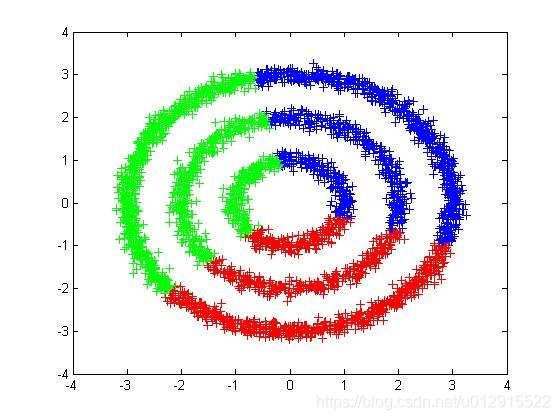
图2 K-Means在非凸集上聚类出现错误
基于密度的聚类算法很好的解决了这个问题,能够在非凸集合上获得很好的聚类结果。DBSCAN(Density-Based Spatial Clustering of Application with Noise)算法就是一种典型基于密度的聚类算法。
3.1 样本点类别
定义样本点 X ( i ) X^{(i)} X(i)的 ϵ \epsilon ϵ邻域如下:
d i s t ( X , X ( i ) ) ≤ ϵ dist(X,X^{(i)})\le\epsilon dist(X,X(i))≤ϵ
那么定义样本点 X ( i ) X^{(i)} X(i)的密度为样本点 X ( i ) X^{(i)} X(i)的 ϵ \epsilon ϵ邻域内样本个数,如下所示
N ξ ( X ( i ) ) = { X ( j ) ∣ d i s t ( X ( j ) , X ( i ) ) ≤ ϵ } N_\xi(X^{(i)})=\{X^{(j)}|dist(X^{(j)}, X^{(i)})\le\epsilon\} Nξ(X(i))={X(j)∣dist(X(j),X(i))≤ϵ}
通过与设定密度下限 m i n P t s minPts minPts对比,将样本点分为三类:
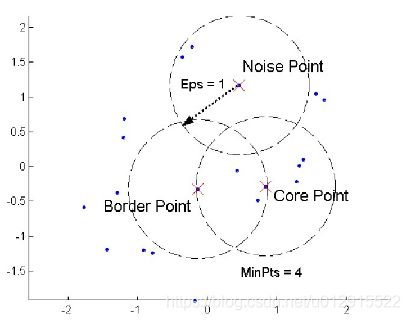
- 核心点(core points):样本点 X ( i ) X^{(i)} X(i)处的密度大于密度下限;
- 边界点(border points):样本点 X ( i ) X^{(i)} X(i)处的密度小于密度下限,但是样本点 X ( i ) X^{(i)} X(i)在某一核心点的邻域内;
- 噪声点(Noise):既不是核心点也不是样本点。
3.2 直接密度可达、密度可达、密度连接
观察实际的问题,如下图
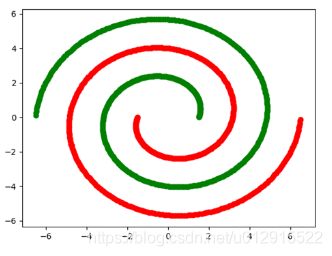
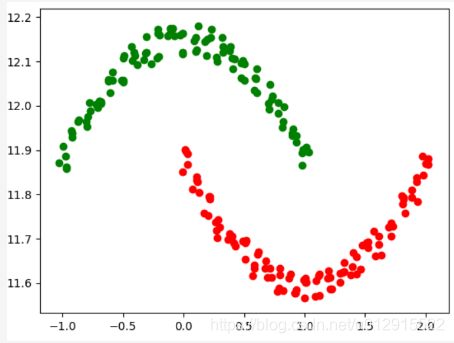
图3 典型非凸集聚类问题
图片摘自DBSCAN密度聚类(https://www.cnblogs.com/king-lps/p/7816686.html)
那么不难发现一个规律,就是在聚类问题中,样本点之间存在密度很低区域(图3中白色区域),那么基于密度的聚类算法,本质上时寻找被低密度区域分割的高密度区域,并将高密度区域聚类成簇。
结合样本点的类别,可以将上述原理再重新表述:DBSCAN聚类算法本质上就是通过寻找一系列的紧紧挨着的高密度核心点(core points),以及这批核心点外层的边界点,将其聚类成簇。
那么紧紧挨着该如何定义呢?
以下图为例(minPts=5),与核心点 A A A的挨得最近的肯定是 A A A的 ϵ \epsilon ϵ邻域内的点(灰色点),其次像类似 B 、 E B、E B、E这样的点,与 A A A共同属于一个高密度区域,是紧紧相挨着的核心点, F F F和 A A A共同属于一个高密度区域,但是 F F F不是核心点,而是边界点,所以 F F F就是紧紧挨着 A A A的边界点。 Z Z Z和 A A A属于不同高密度区域,所以非挨着 A A A得核心点。
(这段话是不是很绕口,没关系,我们先由此定义一些概念)
直接密度可达:
所有在核心点 A A A的 ϵ \epsilon ϵ邻域内的点,称为从 A A A直接密度可达的点。(A必须是核心点)
密度可达:
从 X i , 1 X_{i,1} Xi,1到 X i , n X_{i,n} Xi,n中间存在一系列点 X i , 2 , . . . , X i , n − 1 X_{i,2},...,X_{i,n-1} Xi,2,...,Xi,n−1,且这一系列点满足 ( X i , j , X i , j + 1 ) , j = 1 , . . . , n − 1 (X_{i,j},X_{i,j+1}),j=1,...,n-1 (Xi,j,Xi,j+1),j=1,...,n−1是直接密度可达,那么称 X i , 1 X_{i,1} Xi,1与 X i , n X_{i,n} Xi,n是密度可达的。(一系列 X i , 1 , . . . , X i , n − 1 X_{i,1},...,X_{i,n-1} Xi,1,...,Xi,n−1都是核心点)
密度连接: 从 X i X_i Xi点到 X j X_j Xj中间存在 X k X_k Xk点, X i 、 X j X_i、X_j Xi、Xj分别与 X k X_k Xk是密度可达的,称 X i X_i Xi点到 X j X_j Xj点是密度相连的。
那么在图中 C C C和 E E E等在 A A A的 ϵ \epsilon ϵ邻域内,是从 A A A直接密度可达的点。 A 、 B 、 C 、 E A、B、C、E A、B、C、E点是相互密度可达的,而 F F F点是从 A A A点密度可达的。 G G G与 F F F点是密度相连的。
DBSCAN算法的本质就是从核心点 A A A出发寻找密度可达的所有点,将其聚类簇。

3.3 DBSCAN算法过程
输入:
训练样本为 T = { X ( 1 ) , X ( 2 ) , . . . , X ( m ) } T=\{X^{(1)},X^{(2)},...,X^{(m)}\} T={X(1),X(2),...,X(m)},其中 X ( i ) = ( x 1 ( i ) , x 2 ( i ) , . . . , x l ( i ) ) X^{(i)}=(x_1^{(i)},x_2^{(i)},...,x_l^{(i)}) X(i)=(x1(i),x2(i),...,xl(i)),邻域半径 ϵ \epsilon ϵ,密度下限MinPts。
过程:
1.计算所有样本点互相的距离矩阵 D D D:
D = [ ( X ( 1 ) − X ( 1 ) ) 2 ( X ( 2 ) − X ( 1 ) ) 2 ⋯ ( X ( m ) − X ( 1 ) ) 2 ( X ( 1 ) − X ( 2 ) ) 2 ( X ( 2 ) − X ( 2 ) ) 2 ⋯ ( X ( m ) − X ( 2 ) ) 2 ⋮ ⋮ ⋮ ( X ( 1 ) − X ( m ) ) 2 ( X ( 2 ) − X ( m ) ) 2 ⋯ ( X ( m ) − X ( m ) ) 2 ] D=\begin{bmatrix} (X^{(1)}-X^{(1)})^2 & (X^{(2)}-X^{(1)})^2 &\cdots&(X^{(m)}-X^{(1)})^2 \\(X^{(1)}-X^{(2)})^2 & (X^{(2)}-X^{(2)})^2 &\cdots &(X^{(m)}-X^{(2)})^2 \\ \vdots & \vdots & &\vdots \\(X^{(1)}-X^{(m)})^2 & (X^{(2)}-X^{(m)})^2&\cdots &(X^{(m)}-X^{(m)})^2 \end{bmatrix} D=⎣⎢⎢⎢⎡(X(1)−X(1))2(X(1)−X(2))2⋮(X(1)−X(m))2(X(2)−X(1))2(X(2)−X(2))2⋮(X(2)−X(m))2⋯⋯⋯(X(m)−X(1))2(X(m)−X(2))2⋮(X(m)−X(m))2⎦⎥⎥⎥⎤
2.计算样本点 X ( i ) X^{(i)} X(i)的 ϵ \epsilon ϵ邻域,并计算密度;
3.若为样本点 X ( i ) X^{(i)} X(i)为非核心点,则标记,为核心点,则做以下步骤:
① 将所有直接密度可达的样本点标记为同一类别;
② 从这些点中计算是不是另一个核心点,如果是,则将该核心点内的所有点标记为同一类别,如果不是,则跳过;
③ 直到 X ( i ) X^{(i)} X(i)的 ϵ \epsilon ϵ邻域内所有样本点都被搜索完;
4.重复上述过程,直到核心点均被处理,将未处理的样本点标记为噪声点。
输出:
聚类完的标签向量Label
3.4 DBSCAN算法Python代码实现
输入样本集如下:
1.658985 4.285136
-3.453687 3.424321
4.838138 -1.151539
-5.379713 -3.362104
...
-2.793241 -2.149706
2.884105 3.043438
-2.967647 2.848696
4.479332 -1.764772
-4.905566 -2.911070
首先需要实现 ϵ \epsilon ϵ邻域计算,包括距离矩阵计算和邻域内样本点的获取。
def distance(data):
m = data.shape[0]
dis = np.zeros((m,m))
for loopi in range(int(data.shape[0])):
for loopj in range(loopi+1,int(data.shape[0])):
# vector = X(i)-X(j)
vector = data.iloc[loopi] - data.iloc[loopj]
dis[loopi, loopj] = np.dot(vector, vector)
dis = np.sqrt(dis + dis.T)
return dis
def find(dis,epsilon):
index = []
for loop in range(len(dis)):
if d[loop]<epsilon:
index.append(loop)
return index
DBSCAN算法主程序如下,依次从核心点出发找到所有密度可达的点,直到所有的核心点都被处理
def dbscan(data,epsilon,minpts):
m = data.shape[0]
dealed = np.zeros((m, 1))
label = np.zeros((m,1))
nodetype = np.zeros((m,1))
dis = distance(data)
number = 1
for index in range(int(data.shape[0])):
#node is not dealed
if(dealed[index]==0):
d = dis[index,:]
#index2 is a list node ID of X(index)'s e-domain
index2 = find(d, epsilon)
if len(index2)<2:
# noise
dealed[index] = 1
nodetype[index] = -1
elif len(index2)<minpts:
# not core point, maybe noise or bonder
dealed[index] = 1
nodetype[index] = 0
elif(len(index2)>minpts-1):
# core point
dealed[index] = 1
nodetype[index, 0] = 1
for loopi in index2:
label[loopi, 0] = number
while len(index2):
# figure out the undealed node in e-domain
if(dealed[index2[0], 0]==0):
dealed[index2[0]] = 1
d = dis[index2[0], :]
index_temp = find(d, epsilon)
if (len(index_temp)>minpts):
# core point
for loopj in index_temp:
label[loopj, 0] = number
if(dealed[loopj]==0 and (loopj not in index2)):
index2.append(loopj)
elif(len(index_temp)>1):
# not core point
for loopj in index_temp:
label[loopj, 0] = number
dealed[loopj] = 1
del index2[0]
number += 1
return label
结果如下,结果显示随 ϵ \epsilon ϵ值减小,聚类相对集中,噪声点变多,而随 m i n P t s minPts minPts值增大,聚类相对集中,噪声点变多,最终好的结果取决于怎么取到合适的参数。
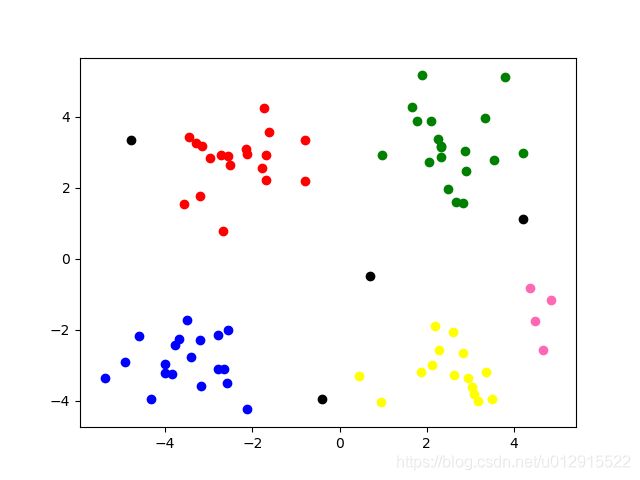

ϵ = 1.3 , m i n P t s = 4 \epsilon=1.3,minPts=4 ϵ=1.3,minPts=4 ϵ = 0.8 , m i n P t s = 4 \epsilon=0.8,minPts=4 ϵ=0.8,minPts=4
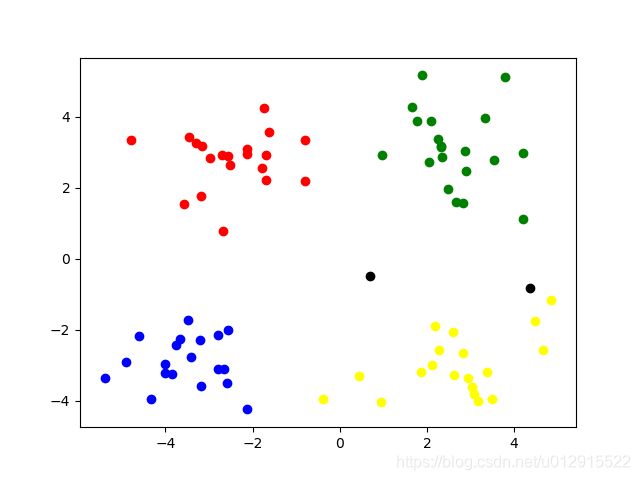

ϵ = 1.5 , m i n P t s = 5 \epsilon=1.5,minPts=5 ϵ=1.5,minPts=5 ϵ = 0.8 , m i n P t s = 5 \epsilon=0.8,minPts=5 ϵ=0.8,minPts=5
附录:Python源代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
def distance(data):
m = data.shape[0]
dis = np.zeros((m,m))
for loopi in range(int(data.shape[0])):
for loopj in range(loopi+1,int(data.shape[0])):
vector = data.iloc[loopi] - data.iloc[loopj]
dis[loopi, loopj] = np.dot(vector, vector)
dis = np.sqrt(dis + dis.T)
return dis
def find(d,epsilon):
index = []
for loop in range(len(d)):
if d[loop]<epsilon:
index.append(loop)
return index
def dbscan(data,epsilon,minpts):
m = data.shape[0]
dealed = np.zeros((m, 1))
label = np.zeros((m,1))
nodetype = np.zeros((m,1))
dis = distance(data)
number = 1
for index in range(int(data.shape[0])):
if(dealed[index]==0):
d = dis[index,:]
index2 = find(d, epsilon)
if len(index2)<2:
dealed[index] = 1
nodetype[index] = -1
elif len(index2)<minpts:
dealed[index] = 1
nodetype[index] = 0
elif(len(index2)>minpts-1):
dealed[index] = 1
nodetype[index, 0] = 1
for loopi in index2:
label[loopi, 0] = number
while len(index2):
if(dealed[index2[0], 0]==0):
dealed[index2[0]] = 1
d = dis[index2[0], :]
index_temp = find(d, epsilon)
print(index_temp)
if (len(index_temp)>minpts):
for loopj in index_temp:
label[loopj, 0] = number
if(dealed[loopj]==0 and (loopj not in index2)):
index2.append(loopj)
elif(len(index_temp)>1):
for loopj in index_temp:
label[loopj, 0] = number
dealed[loopj] = 1
del index2[0]
number += 1
return label
if __name__=='__main__':
data = []
with open(r'x\data.txt') as f:
for line in f.readlines():
line = line.strip().split('\t')
temp = [float(line[0]),float(line[1])]
data.append(temp)
data = pd.DataFrame(data, columns=['x', 'y'])
label = dbscan(data, 0.8, 5)
label = pd.DataFrame(label, columns=['label'])
data = pd.concat([data, label], axis=1)
labelnum = max(data.label)
colors = ['black','green', 'red', 'blue','yellow', 'hotpink']
for loopi in range(1,int(labelnum)+1):
plt.scatter(data[data.label==loopi].x, data[data.label==loopi].y, color=colors[loopi])
plt.scatter(data[data.label == 0].x, data[data.label == 0].y, color=colors[0])
plt.scatter(data[data.label == -1].x, data[data.label == -1].y,color=colors[0])
plt.show()
# data set
1.658985 4.285136
-3.453687 3.424321
4.838138 -1.151539
-5.379713 -3.362104
0.972564 2.924086
-3.567919 1.531611
0.450614 -3.302219
-3.487105 -1.724432
2.668759 1.594842
-3.156485 3.191137
3.165506 -3.999838
-2.786837 -3.099354
4.208187 2.984927
-2.123337 2.943366
0.704199 -0.479481
-0.392370 -3.963704
2.831667 1.574018
-0.790153 3.343144
2.943496 -3.357075
-3.195883 -2.283926
2.336445 2.875106
-1.786345 2.554248
2.190101 -1.906020
-3.403367 -2.778288
1.778124 3.880832
-1.688346 2.230267
2.592976 -2.054368
-4.007257 -3.207066
2.257734 3.387564
-2.679011 0.785119
0.939512 -4.023563
-3.674424 -2.261084
2.046259 2.735279
-3.189470 1.780269
4.372646 -0.822248
-2.579316 -3.497576
1.889034 5.190400
-0.798747 2.185588
2.836520 -2.658556
-3.837877 -3.253815
2.096701 3.886007
-2.709034 2.923887
3.367037 -3.184789
-2.121479 -4.232586
2.329546 3.179764
-3.284816 3.273099
3.091414 -3.815232
-3.762093 -2.432191
3.542056 2.778832
-1.736822 4.241041
2.127073 -2.983680
-4.323818 -3.938116
3.792121 5.135768
-4.786473 3.358547
2.624081 -3.260715
-4.009299 -2.978115
2.493525 1.963710
-2.513661 2.642162
1.864375 -3.176309
-3.171184 -3.572452
2.894220 2.489128
-2.562539 2.884438
3.491078 -3.947487
-2.565729 -2.012114
3.332948 3.983102
-1.616805 3.573188
2.280615 -2.559444
-2.651229 -3.103198
2.321395 3.154987
-1.685703 2.939697
3.031012 -3.620252
-4.599622 -2.185829
4.196223 1.126677
-2.133863 3.093686
4.668892 -2.562705
-2.793241 -2.149706
2.884105 3.043438
-2.967647 2.848696
4.479332 -1.764772
-4.905566 -2.911070
文章导引列表:
机器学习
- 小瓜讲机器学习——分类算法(一)logistic regression(逻辑回归)算法原理详解
- 小瓜讲机器学习——分类算法(二)支持向量机(SVM)算法原理详解
- 小瓜讲机器学习——分类算法(三)朴素贝叶斯法(naive Bayes)
- 小瓜讲机器学习——分类算法(四)K近邻法算法原理及Python代码实现
- 小瓜讲机器学习——分类算法(五)决策树算法原理及Python代码实现
- 小瓜讲机器学习——聚类算法(一)K-Means算法原理Python代码实现
- 小瓜讲机器学习——聚类算法(二)Mean Shift算法原理及Python代码实现
- 小瓜讲机器学习——聚类算法(三)DBSCAN算法原理及Python代码实现
数据分析
- 小呆学数据分析——使用pandas中的merge函数进行数据集合并
- 小呆学数据分析——使用pandas中的concat函数进行数据集堆叠
- 小呆学数据分析——pandas中的层次化索引
- 小呆学数据分析——使用pandas的pivot进行数据重塑
- 小呆学数据分析——用duplicated/drop_duplicates方法进行重复项处理
- 小呆学数据分析——缺失值处理(一)
- 小呆学数据分析——异常值判定与处理(一)
- 小瓜讲数据分析——数据清洗
数据可视化
- 小瓜讲数据分析——数据可视化工程(matplotlib库使用基础篇)
- 小瓜讲matplotlib高级篇——坐标轴设置(坐标轴居中、坐标轴箭头、刻度设置、标识设置)