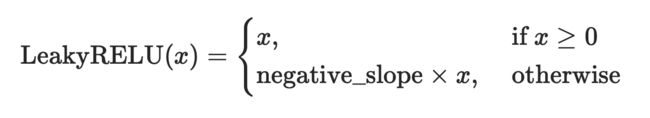Pytorch学习笔记——kaiming_uniform初始化
文章目录
- 前言
- kaiming_uniform
-
- 模型定义
- 参数说明
- 官方文档
- 1. leaky_relu
-
- 函数图像
- 计算公式
- LeakyReLU模型定义
- 参数说明
- Pytorch代码示例
- 2. a参数
前言
在Pytorch的Linear层实现代码中,使用了kaiming均匀初始化,调用代码如下。
init.kaiming_uniform_(
self.weight,
a=math.sqrt(5))
本文是学习这个初始化方法的笔记。
kaiming_uniform
模型定义
torch.nn.init.kaiming_uniform_(
tensor,
a=0,
mode='fan_in',
nonlinearity='leaky_relu'
)
参数说明
tensor:输入张量
a:该层之后使用的整流器的负斜率(仅与"leaky_relu"一起使用)
mode:“fan_in”(默认)或"fan_out"。选择"fan_in"可以保留前向计算中权重方差的大小。选择"fan_out"将保留后向传播的方差大小。
nonlinearity:非线性函数,建议仅与"relu"或"leaky_relu"(默认)一起使用。
官方文档
下面,逐个参数进行学习,首先是leaky_relu。
1. leaky_relu
Leaky Rectized Linear Unit或Leaky ReLU是一种基于ReLU的激活函数,但它具有较小的负值斜率,而不是平坦的斜率。斜率系数在训练前确定,即在训练期间不学习。这种类型的激活函数在我们可能遭受稀疏梯度的任务中很受欢迎。
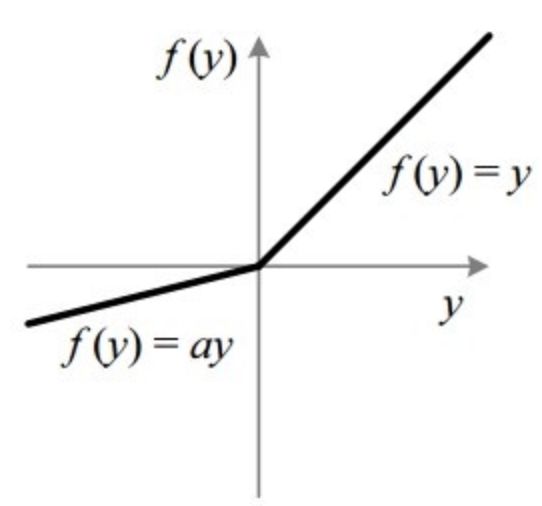
函数图像
计算公式
LeakyReLU模型定义
torch.nn.LeakyReLU (
negative_slope=0.01,
inplace=False
)
参数说明
negative_slope:负值斜率,指定后不改变
inplace:是否原地操作数据,默认值:False
Pytorch代码示例
>>> m = nn.LeakyReLU(0.1)
>
>>> input = torch.tensor([1.2, -0.5])
>>> input
tensor([ 1.2000, -0.5000])
>>> output = m(input)
>>> output
tensor([ 1.2000, -0.0500])
# 注意 -0.5 变为 -0.05
从上面的代码中可以看到,正数保持不变,但是负数变为原来的0.1倍。
2. a参数
a代表LeakyReLU的负值斜率。
重新审视一下Linear模型中kaiming_uniform的参数,a传入了sqrt(5)。
init.kaiming_uniform_(
self.weight,
a=math.sqrt(5)
)
那么,最终我们得到的均匀分布是怎么样的呢?
根据上面的公式可以计算一下kaiming均匀分布的上下界。
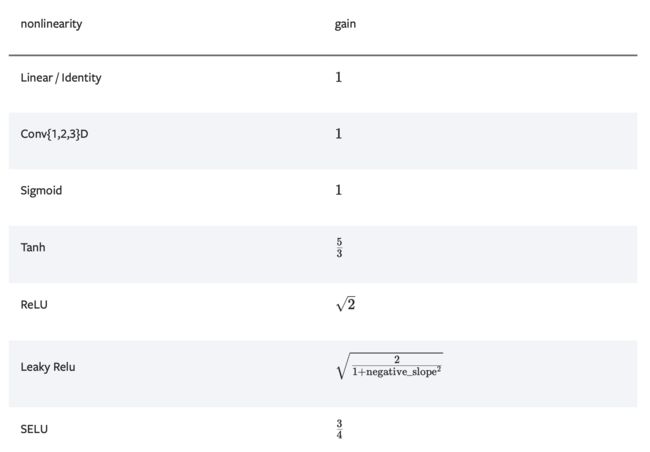
因为: b o u n d = g a i n × 3 f a n _ m o d e {\text bound} =gain \times \sqrt{ \cfrac 3 {\text fan\_mode}} bound=gain×fan_mode3
对于leaky_rule, gain = 2 1 + n e g a t i v e _ s l o p e 2 \text{gain}=\sqrt{\cfrac {2} {1+negative\_slope^2}} gain=1+negative_slope22
这里代码里指定了 n e g a t i v e _ s l o p 2 = 5 negative\_slop^2 = 5 negative_slop2=5,所以gain= 1 3 \sqrt{\cfrac 1 3} 31
所以,bound= 1 f a n _ m o d e \sqrt{ \cfrac 1 {fan\_mode}} fan_mode1