Count Primes

https://leetcode.com/problems/count-primes/

Description:

Count the number of prime numbers less than a non-negative number, n.

解题思路：

如何判定一个数为质数？1. 质数最小的是2。2.质数的定义是，除了1和他自己，没有其他数能整除它。

很容易想到最朴素的解法，从2到n-1，每个数字i都用2到i-1的数字去除，有一个可以整除它，就不是质数。

这个解法时间复杂度为O(n^2)。想想会有不少能改进的地方。

1. 不用2到i-1的除。从2到sqrt(i)即可，很容易理解吧。

2. 如果2不能整除，也不用尝试4、6、8……所有的偶数了。

3. 那么除了2以外，只要看质数。但是如果3不能整除，好像6、9、12……也肯定不能整除。5同理。

事实上，这是一个定理。将该数N用小于等于sqrt{N}的所有素数去试除，若均无法整除，则N为素数。原理就是，一个合数的因数，肯定能分解成n个质数的乘积。

也就是，只要用质数去整除他就可以了，当然这里包含了2。 https://zh.wikipedia.org/wiki/%E7%B4%A0%E6%95%B0

解法如下：

这里将前面已经得出的prime都记录下来了，用来继续判断后面的prime。

 

public class Solution {

    public int countPrimes(int n) {

        int count = 0;

        List<Integer> primes = new ArrayList<Integer>();

        for(int i = 2; i < n; i++) {

            boolean isPrime = true;

            // 将该数N用小于等于sqrt{N}的所有素数去试除，若均无法整除，则N为素数

            for(Integer prime : primes) {

                if(prime > Math.sqrt(i)) {

                    break;

                }

                if(i % prime == 0) {

                    isPrime = false;

                    break;

                }

            }

            if(isPrime) {

                count++;

                primes.add(i);

            }

        }

        return count;

    }

}

 

但是，上面的解法还会重复判断。对后面的每个数字，还是要从前面已经得出的所有prime里面，循环再判断一遍。

下面是一个远古希腊大神，埃拉托斯特尼，提出的筛选法。啥叫筛选法，直接表述吧，理解了写代码是很简单。

给出要筛数值的范围n，找出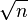以内的素数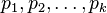。先用2去筛，即把2留下，把2的倍数剔除掉；再用下一个素数，也就是3筛，把3留下，把3的倍数剔除掉；接下去用下一个素数5筛，把5留下，把5的倍数剔除掉；不断重复下去......。

https://zh.wikipedia.org/wiki/%E5%9F%83%E6%8B%89%E6%89%98%E6%96%AF%E7%89%B9%E5%B0%BC%E7%AD%9B%E6%B3%95

 

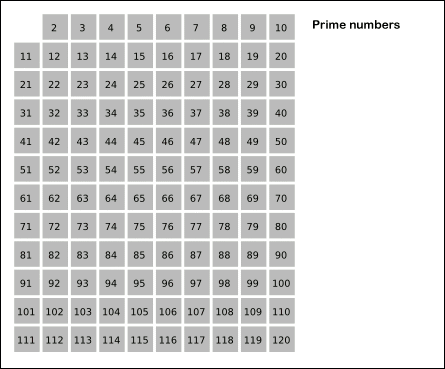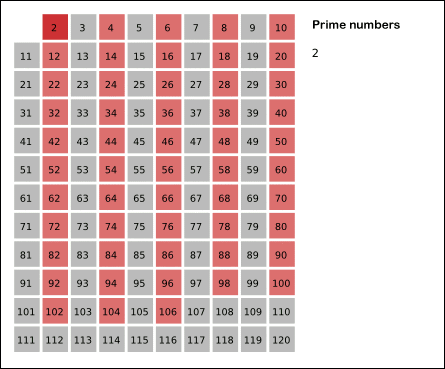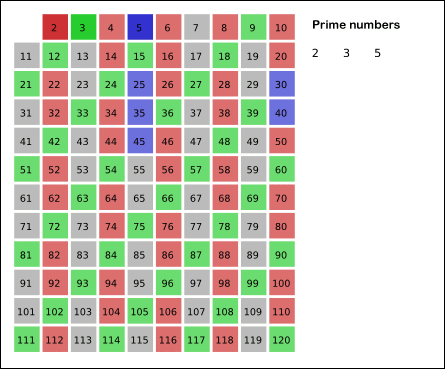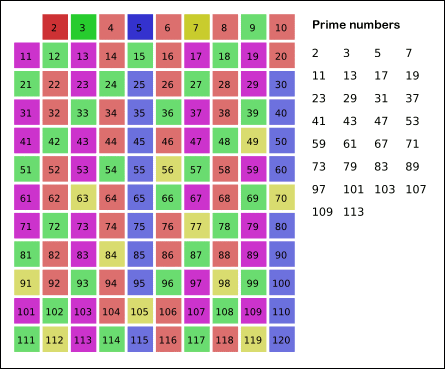
public class Solution {

    public int countPrimes(int n) {

        int count = 0;

        int[] filter = new int[n];//0是质数，1不是

        for(int i = 2; i < n; i++) {

            if(filter[i] == 1) {

                continue;

            }

            count++;

            for(int j = i * 2; j < n; j = j + i) {

                filter[j] = 1;

            }

        }

        return count;

    }

}

 http://program-think.blogspot.com/2011/12/prime-algorithm-1.html