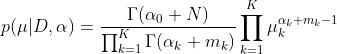【Basis】狄利克雷分布
初次看狄利克雷分布,比较懵,主要是它有很多先行知识,所以我先介绍狄利克雷分布用到的多项式分布、gamma 函数、beta分布,然后再介绍狄利克雷分布。参考文献见文章末。
目录
一、多项式分布 multinomial distribution
1.1 假设 Assumption
1.2 推导 infer
二、伽马函数 Gamma Function
2.1 任务
2.2 证明过程
三、贝塔分布 Beta Distribution
3.1 beta公式推导
3.2 Beta和gamma function之间的关系
四、狄利克雷分布 Dirichlet Distribution
4.1 假设 Assumption
4.2 推导 infer
参考文献
一、多项式分布 multinomial distribution
1.1 假设 Assumption
假设随机变量![]() 的状态(state)有
的状态(state)有![]() 种,每种状态记作
种,每种状态记作![]() ,比如当
,比如当![]() 处于第三种状态时,
处于第三种状态时,![]() =1,其余都等于0,即:
=1,其余都等于0,即:![]() ,即
,即![]() (1.1)。每种状态的概率是
(1.1)。每种状态的概率是![]() ,则
,则![]() (1.2)。设
(1.2)。设![]() 。
。
1.2 推导 infer
那么,在给定![]() 的情况下,
的情况下,![]() 的分布服从:
的分布服从:
这是一个随机变量,假设我们有数据集D,D中观测了N次随机变量x,那么
令![]() (1.5),我们可以把
(1.5),我们可以把![]() 理解为N次观测(observation)中,
理解为N次观测(observation)中,![]() 状态为
状态为![]() 的数量!写出似然率
的数量!写出似然率![]() ,我们开始计算极大似然率,以求出唯一不知道的
,我们开始计算极大似然率,以求出唯一不知道的![]() 。值得注意的是
。值得注意的是![]() 本身具有约束条件5.2,所以带有约束条件的极大值问题,我们引入拉格朗日乘子
本身具有约束条件5.2,所以带有约束条件的极大值问题,我们引入拉格朗日乘子![]() (lagrange multiplier)。得到:
(lagrange multiplier)。得到:
![]() (1.6)
(1.6)
求极值的主要方法简单来说就是求导等于0。上式对![]() 求偏导,得到:
求偏导,得到:
易得,![]() (1.8)。将该结果
(1.8)。将该结果![]() 的约束条件,得到
的约束条件,得到![]() ,
,![]() 。由于等式5.1,我们得到
。由于等式5.1,我们得到![]() (1.9)。最终:
(1.9)。最终:
我们可以理解为,每种状态的概率等于N次观测中出现的占比(大数定理简化)。将最终的多项式分布公式写出来:
二、伽马函数 Gamma Function
emmm,其实我也不知道伽马函数是干嘛的,但是狄利克雷分布中出现了,找PRML的书看了一下,长得奇奇怪怪的,但是貌似是两个性质比较重要,需要推导一下。先给出伽马公式:
2.1 任务
利用分部积分法(integration by parts)证明出
①![]()
②![]() (阶乘的推广)
(阶乘的推广)
③![]()
2.2 证明过程
①首先回忆一下分部积分法:
②![]() (2.4)
(2.4)
④![]() (2.6),怎么能跟
(2.6),怎么能跟![]() 联系在一起呢?我们会想到高斯分布中有
联系在一起呢?我们会想到高斯分布中有![]() ,取
,取![]() ,有
,有![]() ,且
,且![]() 。我们令
。我们令![]() ,则
,则
![]() (2.7),
(2.7),![]() 。所以:
。所以:
三、贝塔分布 Beta Distribution
设![]() 为连续随机变量,取值范围(interval)为
为连续随机变量,取值范围(interval)为![]() ,其概率密度函数(pdf)为:
,其概率密度函数(pdf)为:
其中![]() 。而
。而![]() 又被定义为
又被定义为
这个公式怎么来的呢?
3.1 beta公式推导
如果随机变量x服从(falls into)参数为n和p的分布,则有:
根据上面的式子,我们构造函数:
![]() (3.4)
(3.4)
为了让这个函数满足分布的基本性质,我们引入一个归一化因子(normalization coefficient)让它从0到1的积分为1。假设为k
3.2 Beta和gamma function之间的关系
首先,观察公式(3.3),我们知道![]() ,因为概率
,因为概率![]() 不确定,其服从
不确定,其服从![]() ,所以为了求
,所以为了求![]() 的分布,需要对
的分布,需要对![]() 进行积分:
进行积分:
那p(x)等于多少呢?我们引用一个例子,假设我们在一个[0,1]的区间内放一个点,然后在这个点的两边随机取n个点,左边的点数记为x。那么这个案例是符合上式的,我们把这个案例反过来。假设我们先放了n+1个点,那么选择每一个点的概率为![]() 。所以我们可以得到
。所以我们可以得到![]() (3.8)。
(3.8)。
那么![]() (3.9)
(3.9)
令![]() ,则
,则![]() 。有
。有
回顾第二部分gamma function第二条性质,![]() ,所以
,所以
四、狄利克雷分布 Dirichlet Distribution
首先我们要先了解一下另一个名词,共轭分布 conjugate distribution。在贝叶斯概率理论中,如果后验概率和先验概率满足同一种类型的分布,那么,先验分布和后验分布被叫做共轭分布,同时,先验分布叫做似然函数的共轭先验分布。
Beta分布是二项式分布的共轭先验分布,而狄利克雷(Dirichlet)分布是多项式分布的共轭分布。
有了之前的铺垫,狄利克雷分布就可以理解为多维beta分布。
4.1 假设 Assumption
假设随机变量![]() 的状态有
的状态有![]() 种,每种状态记作
种,每种状态记作![]() ,比如当
,比如当![]() 处于第三种状态时,
处于第三种状态时,![]() =1,其余都等于0,即:
=1,其余都等于0,即:![]() ,即
,即![]() (4.1)。每种状态的概率是
(4.1)。每种状态的概率是![]() ,则
,则![]() (4.2)。设
(4.2)。设![]() 。 令
。 令![]() (4.3),我们可以把
(4.3),我们可以把![]() 理解为N次观测中,
理解为N次观测中,![]() 状态为
状态为![]() 的数量。
的数量。
4.2 推导 infer
令![]() ,有
,有![]() 。则
。则
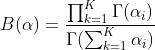 ,则
,则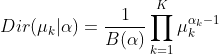 。结合公式1.4,那么最终的后验分布
。结合公式1.4,那么最终的后验分布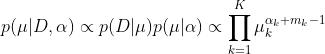 (4.4),依旧服从狄利克雷分布(共轭)。
(4.4),依旧服从狄利克雷分布(共轭)。
最终后验分布为
参考文献
[1]David Bellot. Learning Probabilistic Graphical Models in R. Packt Publishing, 2016
[2] Christopher M. Bishop. Pattern Recognition and Machine Learning.Springer Science+Business Media, LLC,2006
参考博客:(13条消息) 求n的阶乘的算法框图_你不知道的阶乘与gamma函数_weixin_39684967的博客-CSDN博客
https://blog.csdn.net/weixin_39684967/article/details/109980912?utm_source=app&app_version=4.19.0&code=app_1562916241&uLinkId=usr1mkqgl919blen
浅谈狄利克雷分布——Dirichlet Distribution_止于至玄-CSDN博客_狄利克雷分布
https://blog.csdn.net/philthinker/article/details/111999552【统计学进阶知识(一)】深入理解Beta分布:从定义到公式推导 - 知乎 (zhihu.com)
https://zhuanlan.zhihu.com/p/69606875
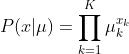
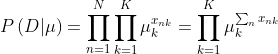
![\Gamma (u+1)=\left [ -x^{u}e^{-x} \right ]_{0}^{+\infty }-\int _{0}^{+\infty }-(u)e^{-x}x^{u}dx=0+u\int _{0}^{+\infty }x^{u}e^{-x}dx=(u)\Gamma (u)](http://img.e-com-net.com/image/info8/bdc1709115584f9b979c31797f4984c2.gif)