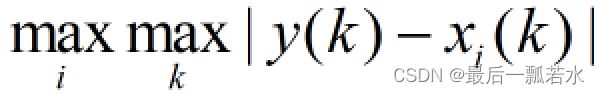灰色关联度

        上一篇写了皮尔逊相关系数、斯皮尔曼相关系数和肯达相关系数的计算代码，本文写一下灰色关联分析的代码。  相关性分析、相关系数矩阵热力图_最后一瓢若水的博客-CSDN博客      

        灰色关联分析是指对一个系统发展变化态势的定量描述和比较的方法，灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密。曲线接近，相应序列之间的关联度就越大，反之就越小

        通常可以运用此方法来分析各个因素对于结果的影响程度（系统分析），也可以运用此方法解决随时间变化的综合评价类问题，其核心是按照一定规则确立随时间变化的母序列，把各个评估对象随时间的变化作为子序列，求各个子序列与母序列的相关程度，依照相关性大小得出结论。（理论部分借鉴其他博客，代码和数据为个人原创，创作目的仅是方便自己日后使用，代码部分如有需要可自取。）

步骤一：清洗数据，数据标准化处理

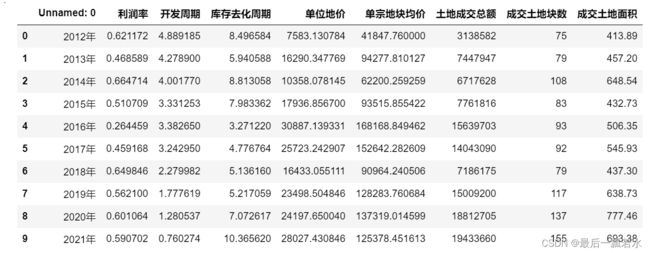
本文所用数据如下图，我们来计算开发周期、库存去化周期、单位低价、单宗地块均价、土地成交总额、成交土地块数、成交土地面积与利润率之间的关联度，故我们需先清除无关数据即时间列数据，然后对数据标准化处理，消除量纲。sklearn库三种标准化与反标准化方法介绍_最后一瓢若水的博客-CSDN博客_sklearn库处理标准化的过程

#读取数据
import pandas as pd
df=pd.read_excel(r"C:\Users\86177\Desktop\datas.xlsx")
df

 清除无关数据后对数据标准化处理，使数据无量纲化。

df=df.iloc[:,1:]#清除第一列无关数据
#数据标准化
import pandas as pd
from sklearn.preprocessing import StandardScaler
columns=df.columns
#Z-score标准化 将某一列数据处理成均值为0，方差为1的数据。优点是受异常值影响较小。公式为：(X-μ)/σ
standard_s1=StandardScaler()#创建StandardScaler()实例
standard_s1_data=standard_s1.fit_transform(df)#将DataFrame格式的数据按照每一个series分别标准化
standard_s1_data_pd=pd.DataFrame(standard_s1_data,columns=columns)#将标准化后的数据改成DataFrame格式
datas=standard_s1_data_pd
datas

步骤二：确定分析数列（参考数列、比较数列）

        确定反映系统行为特征的参考数列和影响系统行为的比较数列。反映系统行为特征的数据序列，称为参考数列。影响系统行为的因素组成的数据序列，称比较数列。

        灰色关联度分析也可以说就是计算比较数列和参数数列之间的关联度，所以本文的例子中参考数列是利润率，比较数列是开发周期、库存去化周期、单位低价、单宗地块均价、土地成交总额、成交土地块数、成交土地面积。

（1）参考数列（又称母数列）：

（2）比较数列（又称子序列）

步骤三：计算关联系数

公式乍一看感觉挺复杂，其实很简单，下面我们把公式分解一下：

（1）

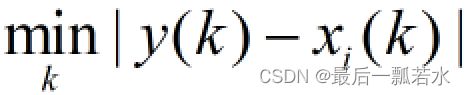是参考数列减去第i个比较数列取绝对值的差数列，然后取差数列的最小值，则是取差数列的最大值。

（2）

是最小差值，就是所有差数列的最小值的最小值，比如我们这里有7个比较数列，就会有7个差数列，每个差数列都会有一个最小值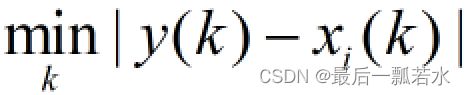，那么这7个最小值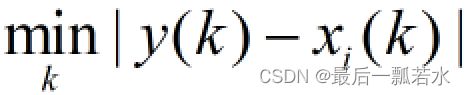里的最小值就是最小差值。

是最大差值，自然就是所有差数列的最大值里的最大值。

（3）

称为分辨系数，ρ越小，分辨力越大，一般ρ的取值区间为(0,1) (0,1)(0,1),具体取值可视情况而定。当ρ≤0.5463时，分辨力最好，通常取ρ=0.5。

总结：当参考数列和比较数列确定后，最小差值和最大差值实际上已经是确定值了，公式中唯一在变的是。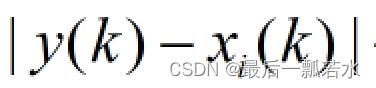

计算最大、最小差值代码：

#计算最小差值和最大差值
rather_columns=columns[1:].tolist()#比较序列
print('比较数列：{}'.format(rather_columns))
min_s=[]#存储参考序列和每一个比较序列的绝对差值的最小值
max_s=[]#存储参考序列和每一个比较序列的绝对差值的最大值
for column in rather_columns:
    min_=(datas['利润率']-datas[column]).abs().min()#比较数列与参考数列矩阵相减后差值的绝对值里的最小值
    max_=(datas['利润率']-datas[column]).abs().max()#比较数列与参考数列矩阵相减后差值的绝对值里的最大值
    min_s.append(min_)
    max_s.append(max_)
print('最小值:{}'.format(min_s))
print('最大值:{}'.format(max_s))
mmin=min(min_s)#最小差值
mmax=max(max_s)#最大差值
print('最小差值:{}'.format(mmin))
print('最大差值:{}'.format(mmax))

 代码结果如下：

计算相关系数矩阵

#计算相关系数矩阵
rho=0.5
for column in rather_columns:
    datas[column]=(mmin+rho*mmax)/(abs(datas['利润率']-datas[column])+rho*mmax)
datas[rather_columns]#相关系数矩阵

结果如下：

 

 步骤四：计算关联度

实际上就是每一列的均值，比如开发周期列的10个数取均值后的平均数，就是开发周期与利润率的关联度。

#计算比较序列与参考序列之间的相关系数
corr=[]
for column in rather_columns:
    corr.append(datas[column].mean())
print('7个比较数列与参考数列的关联度分别为:')
print(corr)

 注：步骤四计算关联度和步骤三计算相关系数矩阵的代码可以合并，分开为了看的更清楚。

完整代码自取:

import pandas as pd
#数据读取与清洗
df=pd.read_excel(r"C:\Users\86177\Desktop\层次分析法所用指标.xlsx")
df=df.iloc[:,1:]
#数据标准化
import pandas as pd
from sklearn.preprocessing import StandardScaler
columns=df.columns
#Z-score标准化 将某一列数据处理成均值为0，方差为1的数据。优点是受异常值影响较小。公式为：(X-μ)/σ
standard_s1=StandardScaler()#创建StandardScaler()实例
standard_s1_data=standard_s1.fit_transform(df)#将DataFrame格式的数据按照每一个series分别标准化
standard_s1_data_pd=pd.DataFrame(standard_s1_data,columns=columns)#将标准化后的数据改成DataFrame格式
datas=standard_s1_data_pd
#计算相关系数
rho=0.5
corr=[]#存储比较序列与参考序列之间的相关系数
for column in rather_columns:
    datas[column]=(mmin+rho*mmax)/(abs(datas['利润率']-datas[column])+rho*mmax)
    corr.append(datas[column].mean())
print(datas[rather_columns])#相关系数矩阵
print('7个比较数列与参考数列的关联度分别为：{}'.format(corr))
#计算比较序列与参考序列之间的相关系数
corr=[]
for column in rather_columns:
    corr.append(datas[column].mean())
print('7个比较数列与参考数列的关联度分别为:')
print(corr)

注：灰色关联读应用在综合评价问题时就是根据比较数列与参考数列的关联度算指标（比较数列）的权重，即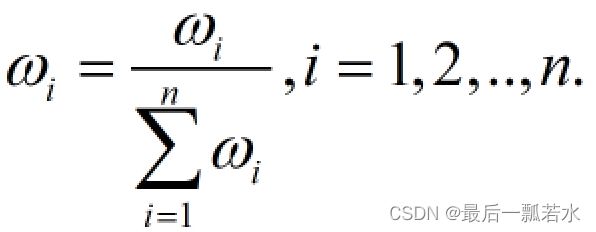，后面有时间总结一下常用的计算权重的方法和代码。