图网络算法——概率图介绍与贝叶斯网络

图网络算法——概率图综述

1 概率论回顾

在介绍概率图之前，我们先来回顾一下概率论中的相关的知识。

样本空间(Ω)： 样本空间描述的是一个随机试验中所有可能输出的集合。比如我们随机抛了一千次硬币，那么我们就可以获得一千次的结果，这一千个结果就构成了样本空间。样本空间中的每一个结果，我们称之为一个样本点。
随机事件： 在样本空间中，某些样本点组成了一个随机事件，即随机事件是样本空间的一个子集。
随机事件之间可能存在的关系：

1. 包含关系：即$A\subset B$，则事件A发生必然会导致事件B发生。
2. 相等关系：即$A<=>B$，事件A和事件B将同时发生。
3. 互不相容：即事件A和事件B不可能同时发生。

随机事件之间的运算：

a. A∪ B，即A与B至少有一个发生。
b. A∩B=AB，即AB同时发生。
c. A-B：即A发生，B不发生。
d. $A^{-}$：对立，即A不发生。

样本空间的分割： 若$A_1,A_2,...A_n$满足以下两个条件：

a. $A_i$之间互不相容
b. $A_1\cup A_2\cup A_3,....\cup A_n=\Omega$
则称$A_1,A_2,...,A_n$是样本空间Ω的一组分割。

概率： 概率指的是某一个事件E的发生满足一个实数值P(E)，这个实数值，我们称之为概率。概率必须要满足下面的三个公理：

a. 对于任意的事件E，其概率$P(E)\ge 0$，即概率用于非负
b. $P(\Omega )=1$，即包含了所有可能的事件的概率为1。
c. 如果多个事件$E_1,E_2,...,$之间相互独立，则有$P({\cup }_{i=1}^{\infty }{E}_i)={\sum }_{i=1}^{\infty }P(E_i)$

**条件概率：**对于事件A，B。如果$P(B)>0$，则称$P(A|B)=\frac{P(AB)}{P(B)}$，为在B出现的条件下，A出现的概率。
进一步，根据条件概率的原始定义，我们可以扩充出三个常见的变换公式：

a. $P(B)>0,P(AB)=P(B)P(A|B)$
b. $P(A)>0,P(AB)=P(A)P(B|A)$
c. $P(A_1,A_2,...,A_{n-1})>0,P(A_1,A_2,...,A_n)=P(A_1)P(A_2|A_1),...,P(A_n|A_1,A_2,...,A_{n-1})$

全概率： 根据条件概率计算公式，我们还可以推导出全概率的计算公式，具体定义如下：
$$P(A)=\sum _{i=1}^{n}P(A{B}_i)=\sum _{i=1}^{n}P(A{B}_i)=\sum _{i=1}^{n}P(B_i)P(A|B_i)$$
即当直接计算P(A)比较困难时，可以将事件A分解成几个小事件，通过小事件的概率，然后进行相加来求最终的概率。小事件$B_i$恰好为样本空间的一组分割，这样可以保证求和公式的成立。

贝叶斯公式： 如果事件$B_1,B_2,...,B_n$对应的是样本空间$\Omega$的一组分割，且$P(A)>0,P(B)>0$，则有：
$$P(B_i|A)=\frac{P(A{B}_i)}{P(A)}=\frac{P(B_i)P(B_i|A)}{P(A)}$$
于此同时，我们可以选择把上面的全概率公式进行带入，从而能够获得下面的公式：
$$P(B_i|A)=\frac{P(B_i)P(A|B_i)}{{\sum }_{i=1}^{n}P(B_i)P(A|B_i)}$$
在上面的公式中，我们称$P(B_i)$为先验概率，而$P(B_i|A)$为后验概率。

事件的独立性： 对于两个事件而言，如果其中的任何一个事件的发生不会影响到另外一个事件的发生，则称两个事件是独立。数学形式的描述如下：
$$P(A|B)=P(A)，P(AB)/P(B)=P(A)，P(AB)=P(A)P(B)$$
即，如果事件满足$P(AB)=P(A)P(B)$，则称两个事件相互独立。

条件独立性： 在给定C的条件下，如果事件A和事件B满足$P(AB|C)=P(A|C)P(B|C)$，则称A,B在给定事件C的条件下相互独立。作为概率图中很重要的一个部分，我们举一个例子来说明一下：

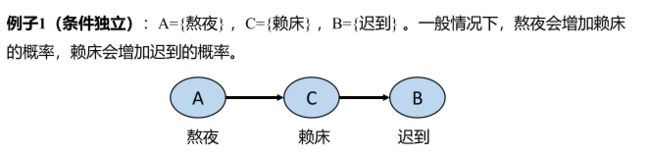
通过上面的例子，我们可以看出，如果给定了赖床的条件C，那么熬夜与迟到之间发生的概率就不会有什么相互的影响了。即在给定C的条件下，事件A与事件B条件独立。

三种常见的概率分布：

1. 联合概率分布：$P(X)=P(X_1,X_2,...X_n)$
   
2. 边缘概率分布：$P(X_a)={\sum }_{X-X_a}P(X)$

3. 最大后验概率(MAP)：$X^{\ast }=argma{x}_{X\in X}P(X)$

2 有向概率图介绍

2.1 有向概率图引入

在正式介绍之前，我们首先来分析一个问题，假设我们现在想要计算随机变量的联合的概率，即P(A,B,C,D)，其中变量A的可能取值有4个，其他三个事件的可能取值有3个。那么对于联合概率P(A,B,C,D)需要考虑到每一个变量的每一个可能的取值情况，那么需要计算的概率结果有$4\ast 3\ast 3\ast 3=108$。这还仅仅包含了四个随机变量，并且每个随机变量的取值范围并不多，随着变量的增加以及事件可能的取值范围的增加，这种计算的复杂度将会呈现指数级的增加。这种复杂度显然我们是无法接受的，那么是否能够简化这种计算呢？ 答案是肯定的，在上面的例子中，我们忽略掉了一个细节，那就不同的变量的独立性与依赖性。举一个极端的例子，假设各个事件都是相互独立的，那么上述的联合概率的计算公式就可以转换为：
$$P(A,B,C,D)=P(A)P(B)P(C)P(D)$$
此时，我们只需要分别计算$P(A),P(B),P(C),P(D)$就可以一次计算出任意的联合概率分布，此时，计算的复杂度也就是4+3+3+3=13，可以看到计算的复杂度有了极大的下降。但是，对于完全独立的多个变量计算联合概率分布还是不常见的。下面我们用一个实际的例子来考虑一下更为常见的情况。

假设当前的随机变量包括季节$(Se)$，鼻子堵塞$(N)$，头痛$(H)$，打喷嚏$(S)$，咳嗽$(C)$，感冒$(Cold)$。假设我们当前需要对这些随机变量进行建模，计算其联合概率分布，计算公式如下：
$$P(Se,N,H,S,C,Cold)$$
假设除了Se有4个取值之外，其他的随机变量的取值均为3个。按照之前的联合概率计算，需要分别计算每一个随机变量的不同取值，则计算的复杂度为42222*2=128。这显然计算规模过大，同时，我们继续考虑这样几种依赖关系，

1. 季节对于打喷嚏和鼻子堵塞是由一定影响的，比如冬天出现这两种症状的人一般会比夏天多。
2. 咳嗽和头痛之间是不存在什么依赖关系的，即这两个随机变量之间是相互独立的。
3. 感冒之后会出现上面的四种症状。
   根据我们的依赖性假设，我们可以把这些随机变量整理成图的结构：
   

上述的这种图结构就被称为是有向的概率图模型。其中每一个节点表示的是一个随机变量，同时每一条边表示的是不同的随机变量之间的相互依赖关系。值得注意的是，这种关系是有向的，即打喷嚏依赖季节，但是季节并不依赖打喷嚏(之后我们会介绍无向的概率图)。

通过概率图的描述，我们可以发现以下几个优势：

1. 图结构相对容易理解，可以直观的发现不同随机变量之间的依赖关系。
2. 通过概率图模型来计算联合概率分布，可以降低计算的复杂度
3. 存在一些图模型的推断和学习算法，有助于我们更好的进行推断和概率计算。

上述的第一个优势很容易理解，第三个优点我们会在后续讲解具体的算法的时候在进行叙述。下面我们重点来关注第二个优势。回到我们之前介绍的例子，我们希望是对这些随机变量进行联合分布建模，即：
$$P(Se,N,H,S,C,Cold)$$
此时，回到我们之前的3个依赖假设和图结构，我们可以看出，对于打喷嚏S的计算，可以转换成条件的形式，即P(S|Se,Cold)，对于鼻子阻塞的计算，也可以转换成条件的形式，即P(N|Se,Cold)，对于咳嗽和头痛的计算则可以分别转换成P(C|Cold)，P(H|Cold)。而Se和Cold不受其他变量的影响，即P(Se),P(Cold)。通过上述的转换，不难发现，转换之后的各个变量是相互独立的，则此时，我们可以将原始的联合概率转换成下面的形式：
$$P(Se,N,H,S,C,Cold)=P(Se)P(S|Se,Cold)P(N|Se,Cold)P(Cold)P(C|Cold)P(H|Cold)$$
我们将右侧各个相乘的元素称为因子，即联合概率转换成了因子乘积的形式。我们从计算量上观察一下，可以发现，因子的计算量为$4+2^3+2^3+2+2^2+2^2=30$。这就极大的降低了参数计算的数量。

2.2 有向概率图总结

一般情况下，有向的概率图模型是对一个联合分布进行建模，同时，根据有向图的中的依赖关系，可以将联合分布转换成多个因子相乘的形式，即：
$$P(X_1,X_2,...,X_n)=\prod _{i=1}^{N}P(X_i|pa(X_i))$$
其中$pa(X_i)$是图中定义的变量$X_i$的父变量子集。所谓的父变量就是在图中，当A指向B的时候，A就是B的父变量。一个节点可能有很多的子节点，也可能有很多父节点。
最后，我们需要注意的一点是：有向图模型中，不能存在环的结构，比如下图所示的形式：

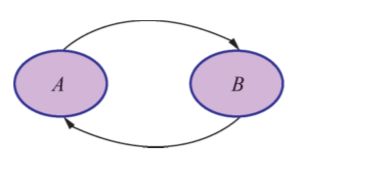
此时，我们在计算因子概率的时候，同时计算的是P(A|B)与P(B|A)，这显然是矛盾的。

3 贝叶斯网络

下面，我们来介绍有向概率图模型中最常见的一个网络结构，即贝叶斯网络。

3.1 贝叶斯网络引入

首先，我们从一个例子开始。对一个学生是否能够拿到老师的推荐信这个问题进行建模。假设当前的随机变量有下面五个，包括“试题难度(Difficulty)，学生智力(Intelligence)，考试成绩(Grade)，高考成绩(SAT)，是否能够得到老师的推荐信(Letter)”。进一步，我们做出下面几个依赖性的假设：

1. 考试成绩依赖于试题的难度，学生的智力。
2. 高考成绩依赖于学生的智力。
3. 是否得到老师的推荐信依赖于开始成绩。

根据上面的描述以及依赖性的假设，我们以上面的随机变量为节点，依赖性作为边，可以构建出一个有向图，如下面所示：

最后，我们给出对于问题的建模为：
$$P(X)=p(D,I,....,L)$$
进一步，我们可以根据依赖关系，将联合概率转换成下面的形式：
$$P(X)=P(D,I,...,L)=P(D)P(I)P(G|D,I)P(S|I)P(L|G)$$

3.2 贝叶斯网络的定义

上述的例子是一个典型的贝叶斯网络，根据上面的例子，我们可以总结出贝叶斯网络的相关定义如下：
贝叶斯网络是一个有向无环图，由代表随机变量的节点和连接这些节点的有向边构成。节点代表随机变量，节点之间的有向边代表了节点之间的相互依赖关系(由父节点指向其子节点)，没有父节点的节点可以采用先验概率进行表示。

进一步，我们令G为定义在$\{X_1,X_2,...,X_N\}$上的一个贝叶斯网络，其联合概率分布可以表示为节点的条件概率或者先验概率的乘积形式，即：
$$P(X)=\prod _i{P}_i(X_i|Pa{r}_G(X_i))$$
其中$Pa{r}_G(X_i)$表示的为节点$X_i$的父节点，$P_i(X_i|Pa{r}_G(X_i)$表示当前节点$X_i$的条件概率。

3.3 贝叶斯网络的例子

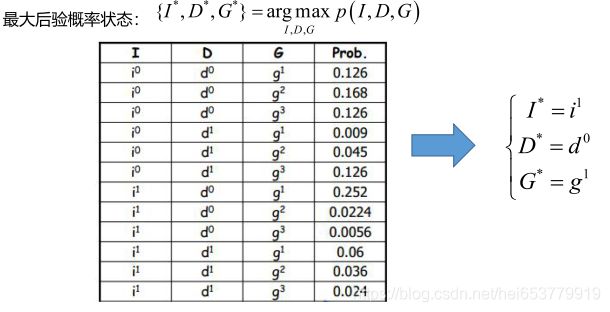
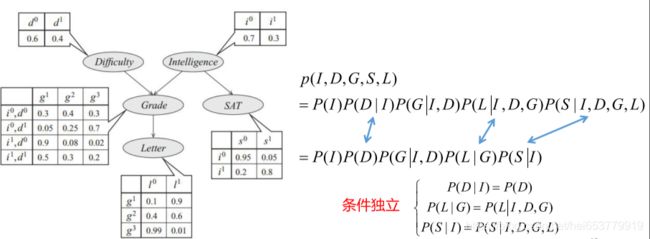
在对贝叶斯网络的概念有了一个基本的了解之后，下面我们回到我们上面所举的例子，此时我们已经利用贝叶斯网络的概念对上面的例子进行了建模，进一步，我们给出一些先验概率和条件概率的结果：

进一步，我们简单的分析一下计算量：

如果采用枚举法，根据每一个随机变量的取值范围，我们的计算量为 $2\ast 2\ast 3\ast 2\ast 3=48$次。
如果采用贝叶斯网络的方法进行计算，对于D和I节点的随机变量的计算都可以通过1次就计算出出来，即P(x)和1-P(x)。对于成绩这个随机变量，根据D和I两个随机变量的4个取值，计算8次就可以计算出$g_1,g_2$，同时可以计算利用$1-g_1-g_2$就可以计算出$g_3$。同样对于随机变量S和随机变量L计算2次即可获取所有结果。即通过贝叶斯的计算，一共的计算次数为$1+1+8+3+2=15$次。可以，计算量得到的大量的减少。

一般地，假设n个二元的随机变量的联合概率分布，表示该分布需要的计算量为$2^n$，如果使用贝叶斯网络进行建模，假设每一个节点最多有k个节点，则所需要的计算量最多为$n\ast 2^k$次，一般每个变量局部依赖于少数变量。

下面，我们举两个联合分布的具体的计算实例，当试题难度较高，学生智力较低，考试成绩高，高考成绩较高，获得推荐信的联合概率结果为：

当试题难度较低，智力较高，高考成绩较高，考试成绩较高，获得老师推荐信的联合概率分布计算为：

3.4 贝叶斯网络概率计算合理性分析

在文章的最后，我们来分析一下，为什么可以将这种联合概率分布转换成局部的条件概率的乘积。这种转换的核心在于条件独立性。我们先来回顾一下条件独立性的例子：

根据上图，我们可以知道，如果给定了随机变量C，我根据条件独立性，我们可以知道：
$$P(B|A,C)=P(B|C)$$
进一步，可以我们给出的联合分布的概率计算公式：
$$P(A_1,A_2,...,A_{n-1})>0,P(A_1,A_2,...,A_n)=P(A_1)P(A_2|A_1),...,P(A_n|A_1,A_2,...,A_{n-1})$$
我们可以将上述例子的联合概率分布转换为：
$$P(A,B.C)=P(A)\ast P(C|A)\ast P(B|C,A)$$
根据条件独立，可以将上述的公式转换为最终的结果：
$$P(A,B.C)=P(A)\ast P(C|A)\ast P(B|C,A)=P(A)P(C|A)P(B|C)$$
根据条件独立，我们可以将全局范围随机变量缩减到局部随机变量，即$P(B|A,C)=P(B|C)$，进一步，我们对不存在父节点的A进行分析，对于A而言，其与随机变量B,C之间并不存在依赖性，用公式表示为：
$$P(A|B,C)=P(A)$$

综上所述，我们证明了贝叶斯网络中联合概率分布转换成多个先验概率和条件概率乘积的合理性。

3.4 贝叶斯网络中的概率流动与独立性

贝叶斯网络中的流动性

首先，我们先来了解两个基本概念：

观测变量： 即在贝叶斯网络中，节点变量的取值可以获取，或者该变量的取值已经确定。
隐变量： 变量的取值未知，通常根据观测变量的取值，对隐变量的取值概率进行推理。

考虑我们之前的条件独立性的例子：

此时，如果C是一个观察变量，那么此时A，B之间的取值不会相互影响。如果C不是观察变量，则A和B的取值是会相互影响的。进一步，我们考虑下面的几种依赖关系：

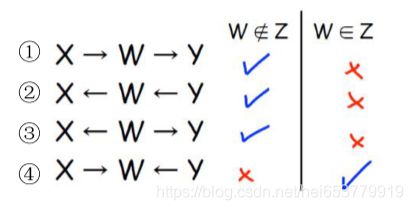
通过判断W是否为观测变量，来分析概率影响的流动性。

1. 在1中，W为观测变量，则此时概率不会相互影响。如果W为非观测变量，此时概率会相互影响。
2. 在2中，W为观测变量，则此时概率不会相互影响，如果W为非观测变量，此时概率会相互影响。
3. 在3中，W为观测变量，则此时概率不会相互影响，如果W为非观测变量，此时概率会相互影响。
4. 在4中，W为观测变量，此时概率会相互影响，如果W为非观测变量，此时概率不会相互影响。
   这里我们来重点分析一下第4项，其实际上可以对应到上面的例子中的成绩变量受到试题难度和学生智商两个方面的影响。如果此时成绩已经确定。即上图中的g已经被确定，此时i，d之间的变化是被互相影响的，比如g取值为$g_2$，此时当i确定时，势必会影响到d的取值。 而当g不确定的时候，i和d的取值不会有什么交集，只是两者的不同的取值会对g产生影响。

贝叶斯网络中的独立性：

有效迹： 对于贝叶斯网络中的一条路径$X_1<=>,...,<=>X_n$和其中的观测变量的子集$Z$，当$X_1$和$X_n$的取值能够相互影响的时候，称路径是有效的。

条件独立与有效迹： 当$X_1<=>,...,<=>X_n$不是有效迹时($X_1$和$X_n$的取值无法相互影响的时候)，$X_1$和$X_n$相互独立。

d-分离： 若图G在给定Z条件下，节点X和Y之间不存在任何有效迹，则称X和Y在给定Z时是d-分离的，记为$d-se{p}_G(X,Y|Z)$

定理： 若概率图G满足$d-se{p}_G(X,Y|Z)$，则X与Y条件独立。

引理： 当父节点已知的时候，该节点与其所有非后代节点满足d-分离。举一个例子来说：

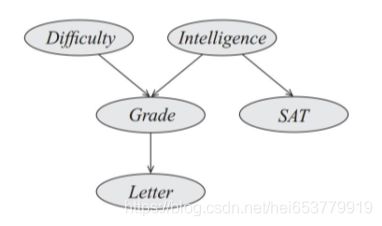
对上上图中，当学生智力随机变量确定的时候，高考成绩SAT与成绩，试题难度，是否获得推荐信等随机变量是满足d-分离的。

定理： 当父节点已知的时候，该节点与其所有的非后代节点条件独立。

根据条件独立，我们可以推论出贝叶斯网络中的链式法则，继续以上面为例，可以得到如下的形式：

3.5 贝叶斯网络总结

通过上面的例子，我们给出的贝叶斯网络的基本概念，并且分类贝叶斯网络中节点的概率的流动性，节点的独立性，并根据条件独立性给出了贝叶斯网络中的链式法则。

4 参考

1. 董建家 概率图模型理论与应用