施密特正交化的几何解释与代码实现
正交化,简单地说,就是指把若干向量转化成互相之间夹角为90度的状态,这样互相之间没有影响。否则,不满足正交性的因子,相互会影响各自的回归系数,从而可能导致回归系数过大等估计误差,从而影响该因子的评价。
这里讨论最常见的施密特正交化。
1、施密特正交化的几何解释
给定一组基α1,α2,…,αn,将其变换成另外一组正交基β1,β2,…,βn,使这两组基等价
施密特正交化方法:
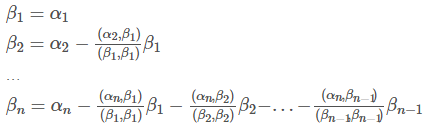
1)在二维的情况下
如图红色部分即为投影部分

则蓝色部分向量为
![]()
对应两个向量的施密特法则

可见蓝色向量 β2 与β1是垂直的。
以上公式也可以推算得到。
先令向量 β1 = α1,只要找到另外一个新的向量 β2,使得 β2 与 β1 内积为0,这两个向量就是正交的了。如何寻找?
根据向量之间的运算关系,因为 β2 由 β1、α2 得到,则我们可以设
β 2 = k 1 β 1 + k 2 β 2 \beta_2=k_1\beta_1+k_2\beta_2 β2=k1β1+k2β2
因为 β2 与 β1 内积为0,因此
( β 1 , β 2 ) = ( β 1 , k 1 β 1 + k 2 β 2 ) = 0 (\beta_1,\beta_2)=(\beta_1,k_1\beta_1+k_2\beta_2)=0 (β1,β2)=(β1,k1β1+k2β2)=0
则有
⇒ k 1 ( β 1 , β 1 ) + k 2 ( β 2 , α 1 ) = 0 \Rightarrow k_1(\beta_1,\beta_1)+k_2(\beta_2,\alpha_1)=0 ⇒k1(β1,β1)+k2(β2,α1)=0
⇒ k 1 = − k 2 ( α 2 , β 1 ) ( β 1 , β 1 ) \Rightarrow k_1=-\frac{k_2(\alpha_2,\beta_1)}{(\beta_1,\beta_1)} ⇒k1=−(β1,β1)k2(α2,β1)
因此
β 2 = k 2 α 2 − k 2 ( α 2 , β 1 ) ( β 1 , β 1 ) α 1 \beta_2=k_2\alpha_2-\frac{k_2(\alpha_2,\beta_1)}{(\beta_1,\beta_1)}\alpha_1 β2=k2α2−(β1,β1)k2(α2,β1)α1
令 k = 1,就得到了新的正交向量 β 1 \beta_1 β1与 β 2 \beta_2 β2。
举个栗子(没看错,是举着栗子。。。),现有矩阵 [a, b]
a = [ 1 1 1 ] a=\left[ \begin{matrix} 1\\ 1 \\ 1\\ \end{matrix} \right] a=⎣⎡111⎦⎤, b = [ 1 0 2 ] b=\left[\begin{matrix} 1\\0\\2\\ \end{matrix} \right] b=⎣⎡102⎦⎤
根据以上公式有:
A = a
B = b − A T b A T A A B=b-\frac{A^Tb}{A^TA}A B=b−ATAATbA
代入具体数值,有
A = [ 1 1 1 ] A=\left[ \begin{matrix} 1\\ 1 \\ 1\\ \end{matrix} \right] A=⎣⎡111⎦⎤
B = [ 1 0 2 ] − [ 111 ] [ 1 0 2 ] [ 111 ] [ 1 1 1 ] [ 1 1 1 ] = [ 0 − 1 1 ] B=\left[\begin{matrix} 1\\0\\2\\ \end{matrix} \right]-\frac{[1 1 1]\left[\begin{matrix} 1\\0\\2\\ \end{matrix} \right]}{[1 1 1]\left[ \begin{matrix} 1\\ 1 \\ 1\\ \end{matrix} \right]}\left[ \begin{matrix} 1\\ 1 \\ 1\\ \end{matrix} \right]=\left[ \begin{matrix} 0\\ -1 \\ 1\\ \end{matrix} \right] B=⎣⎡102⎦⎤−[111][111][111][102]⎣⎡111⎦⎤=⎣⎡0−11⎦⎤
2)在三维的情况下
即向量个数为3时,对应三维空间的几何解释如图 。

其中绿色的为需要正交的原始基αi(α1是红色的因为α1同时也是β1)
将二维得到的β2平移到坐标原点出后则α3在xoy平面的投影即是
![]()
即α3在β1和β2上的投影组成的平行四边形的斜边,则得到的β3就是α3与该投影的向量差,即红色部分的β3,显然可以看出来β1,β2,β3是正交的。
从推算的角度,我们可以令
β 3 = k 1 β 1 + k 2 β 2 + k 3 α 3 \beta_3=k_1\beta_1+k_2\beta_2+k_3\alpha_3 β3=k1β1+k2β2+k3α3
要让 ( β 1 , β 3 ) = 0 (\beta_1,\beta_3)=0 (β1,β3)=0,需要
( β 1 , β 3 ) = k 1 ( β 1 , β 1 ) + k 2 ( β 1 , β 2 ) + k 3 ( β 1 , α 3 ) = 0 (\beta_1,\beta_3)=k_1(\beta_1,\beta_1)+k_2(\beta_1,\beta_2)+k_3(\beta_1,\alpha_3)=0 (β1,β3)=k1(β1,β1)+k2(β1,β2)+k3(β1,α3)=0
⇒ k 1 = − k 3 ( α 3 , β 1 ) ( β 1 , β 1 ) \Rightarrow k_1=-\frac{k_3(\alpha_3,\beta_1)}{(\beta_1,\beta_1)} ⇒k1=−(β1,β1)k3(α3,β1)
要让 ( β 2 , β 3 ) = 0 (\beta_2,\beta_3)=0 (β2,β3)=0,需要
( β 2 , β 3 ) = k 1 ( β 1 , β 2 ) + k 2 ( β 2 , β 2 ) + k 3 ( β 2 , α 3 ) = 0 (\beta_2,\beta_3)=k_1(\beta_1,\beta_2)+k_2(\beta_2,\beta_2)+k_3(\beta_2,\alpha_3)=0 (β2,β3)=k1(β1,β2)+k2(β2,β2)+k3(β2,α3)=0
⇒ k 2 = − k 3 ( α 3 , β 2 ) ( β 2 , β 2 ) \Rightarrow k_2=-\frac{k_3(\alpha_3,\beta_2)}{(\beta_2,\beta_2)} ⇒k2=−(β2,β2)k3(α3,β2)
因此
β 3 = k 3 α 3 − k 3 ( α 3 , β 1 ) ( β 1 , β 1 ) β 1 − k 3 ( α 3 , β 2 ) ( β 2 , β 2 ) β 2 \beta_3=k_3\alpha_3-\frac{k_3(\alpha_3,\beta_1)}{(\beta_1,\beta_1)}\beta_1-\frac{k_3(\alpha_3,\beta_2)}{(\beta_2,\beta_2)}\beta_2 β3=k3α3−(β1,β1)k3(α3,β1)β1−(β2,β2)k3(α3,β2)β2
三维以上空间里的公式以此类推。
2、代码实现
import numpy as np
A = np.array([[1,1,0],[0,1,1],[1,0,1]],dtype=float)
Q = np.zeros_like(A)
m, n = Q.shape
cnt = 0
for a in A.T:
u = np.copy(a)
for i in range(0, cnt):
u -= np.dot(np.dot(Q[:, i].T, a), Q[:, i]) # 减去待求向量在以求向量上的投影
e = u / np.linalg.norm(u) # 归一化
Q[:, cnt] = e
cnt += 1
print(Q)
或者
from scipy import linalg
A = np.array([[1,1,0],[0,1,1],[1,0,1]])
a = linalg.orth(A)
print(np.array(linalg.orth(A),dtype=float))
print(np.dot(A,A.T)-1)
参考:
1、施密特正交化的几何解释
2、自己动手写施密特正交化
3、揭秘施密特正交化