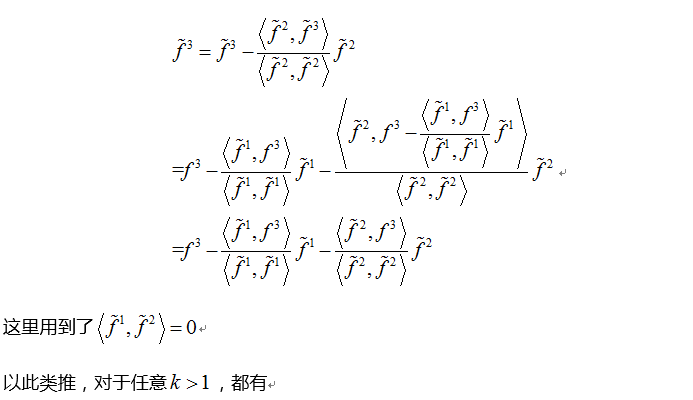施密特正交化_量化投资因子正交化

原创： 量化小白H 量化小白上分记 

本系列的第一篇因子加权方法中提到，对于因子间有相关性的情况，可以通过最大化IR来解决，但也会存在另一个问题：因子协方差矩阵的估计，文中对比了最原始的样本协差阵和Ledoit压缩估计量结果的差异，表明协方差矩阵的估计效果对于结果有很大影响。本文给出另一种更为常用的解决因子间相关性的方法：因子正交化。

01

背景

因子多重共线性

如上一篇所述，传统的多因子模型一般采用IC加权、ICIR加权等方法，这些方法都是以IC为基础确定各因子在模型中的权重。而IC是当期因子暴露与下一期收益间的相关系数。如果因子间存在较强的相关性/相关性，通过上述加权方式，最终会导致因子对于某种风格的因子重复暴露。使得整个组合的表现严重偏向于该因子，削弱其他因子的效果。具体来说，当因子表现好时，组合会获得更高的超额收益，但因子表现不好时，也会出现更大幅的回撤。

举个栗子，在上篇三因子组合市净率、1个月动量、市值的基础上，加入流通市值因子进行四因子组合。采用过去24个月ICIR加权、月度调仓的方式。组合从2012年1月-2018年12月的表现如下

基准采用沪深300指数，显然，四因子组合由于在估摸因子上的重复暴露，导致15年股灾之后，相较于三因子组合出现了超额增长，但在17年规模因子失效后出现了更大回撤。

正交相关定义

首先给出正交相关的一些概念，忘记的可以再翻一翻线性代数/高等代数。

此外，有兴趣可以再去看看正交变换、旋转放缩变换的矩阵表达式，可以加深理解。

因子正交化统一框架

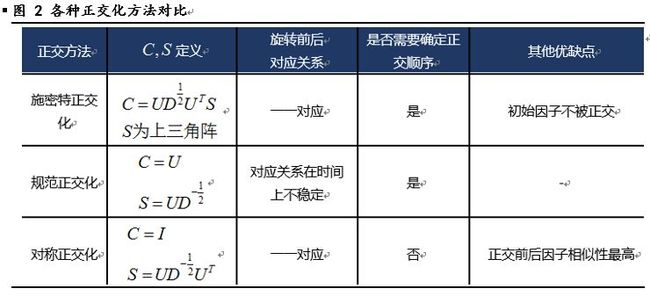
对于因子多重共线性的问题，可以通过因子正交化的方法来解决。因子正交化有多种方式。目前应用最多的有四种：回归取残差、施密特正交化、规范正交化、对称正交化。其中，后三种都是通过因子旋转的方式来消除因子间的相关性，而第一种，后文会给出证明，实质上跟施密特正交化是一致的。因此，首先对后三种正交化方式给出统一说明(这部分参考了报告[1][2]，觉得描述不清楚的可以再去看看报告)：

标准化的意义在于，正交跟不相关的概念本来是不等价的，正交不一定不相关，但加上Z-SCORE标准化之后，正交等价于线性相关系数为0。

以上是因子正交框架，不同的正交化方法具有不同的特性，接下来一一说明，并给出代码。

02

施密特正交化

施密特正交化就是高等代数教科书上的方法，给定一组向量后，分两步操作，第一步按照一定顺序把每个向量与之前所有向量进行正交。第二步对于正交后的向量进行归一化，最终得到的所有向量两两正交且模为1，正交后的因子暴露矩阵为正交阵，用公式表达为

这里给出的代码里正交顺序是直接按照输入因子矩阵的顺序，从左向右依次正交。输入factors为已经标准化后的因子矩阵，返回Q为正交因子矩阵。

# 固定顺序的施密特正交化
   def Schimidt(self,factors):
       class_mkt = factors[['mkt_cap','classname']]
       factors1 = factors.drop(['mkt_cap','classname'],axis = 1)
       col_name = factors1.columns
       factors1 = factors1.values
      
       R = np.zeros((factors1.shape[1], factors1.shape[1]))
       Q = np.zeros(factors1.shape)
       for k in range(0, factors1.shape[1]):
           R[k, k] = np.sqrt(np.dot(factors1[:, k], factors1[:, k]))
           Q[:, k] = factors1[:, k]/R[k, k]
           for j in range(k+1, factors1.shape[1]):
               R[k, j] = np.dot(Q[:, k], factors1[:, j])
               factors1[:, j] = factors1[:, j] - R[k, j]*Q[:, k]

       Q = pd.DataFrame(Q,columns = col_name,index = factors.index)
       Q = pd.concat([Q,class_mkt],axis = 1)
       return Q

注意这里不能用python中的QR分解函数np.linalg.qr计算，施密特正交化是QR分解的一种方法，但numpy的QR分解函数并不是用这种方法做的。

03

回归取残差

回归取残差的方法过程类似施密特正交化，按照一定的顺序将每个向量同之前的所有向量回归取残差代替原值。接下里证明，施密特正交化与最小二乘下的回归取残差是一致的。差别仅在于，施密特正交化多了一步归一化。

04

规范正交化

规范正交化实际上跟主成分分析思路是一样的，但主成分分析在截面上应用可以，用在时间序列上就会出现对应关系不一致的问题，这也是规范正交化的问题。

# 规范正交
   def Canonial(self,factors):
       class_mkt = factors[['mkt_cap','classname']]
       factors1 = factors.drop(['mkt_cap','classname'],axis = 1)
       col_name = factors1.columns     
       D,U=np.linalg.eig(np.dot(factors1.T,factors1))
       S = np.dot(U,np.diag(D**(-0.5)))
       
       Fhat = np.dot(factors1,S)
       Fhat = pd.DataFrame(Fhat,columns = col_name,index = factors.index)
       Fhat = pd.concat([Fhat,class_mkt],axis = 1)        

       return Fhat

05

对称正交化

# 对称正交
   def Symmetry(self,factors):
       class_mkt = factors[['mkt_cap','classname']]
       factors1 = factors.drop(['mkt_cap','classname'],axis = 1)
       col_name = factors1.columns     
       D,U=np.linalg.eig(np.dot(factors1.T,factors1))
       S = np.dot(U,np.diag(D**(-0.5)))
       
       Fhat = np.dot(factors1,S)
       Fhat = np.dot(Fhat,U.T)
       Fhat = pd.DataFrame(Fhat,columns = col_name,index = factors.index)
       Fhat = pd.concat([Fhat,class_mkt],axis = 1)        

       return Fhat

06

方法汇总与对比

对于四因子组合，分别用上述三种因子正交化方法正交之后，组合表现如下

可以看出，对称正交化后的四因子组合表现与三因子表现几乎完全一致，表明对称正交非常完美的剔除了因子相关性的影响，其他三种正交化方法的效果一般，这也与文献【1】【2】中的结论一致。

07

参考文献

【1】20171030-天风证券-天风证券金工专题报告：因子正交全攻略，理论、框架与实践

【2】20180310-光大证券-光大证券多因子系列报告之十：因子正交与择时，基于分类模型的动态权重配置

【3】20170119-海通证券-选股因子系列研究(十七)：选股因子的正交

多因子尝试(一)：因子加权

资产瞎配模型(一)：MVO、风险平价等

资产瞎配模型(二)：对(一)的纠正