RepVGG 核心讲解
论文地址: RepVGG: Making VGG-style ConvNets Great Again (arxiv.org)
主要贡献: 结构重参数化
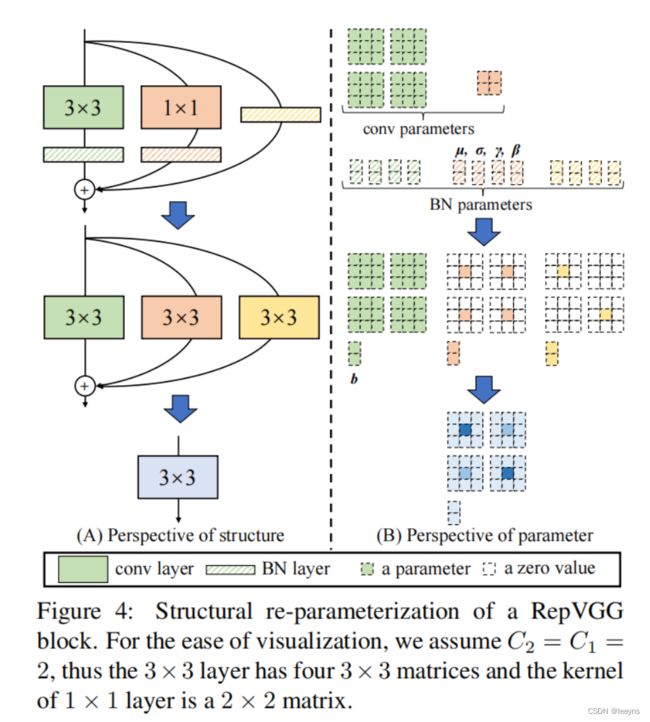
主要结构图
多分支模型的优势
实验证明多分支模型可以更好的增加模型的表征能力,从而提高模型的准确度。文中作者分别试验了baseline, 增加 identity branch和增加 1 × 1 branch的准确度。
单路模型的优势
RepVGG在训练时使用了多分枝模型进行训练,而在推理时使用了结构重参数化,将多分枝模型改为单路模型。
优点:
-
更快
增加并行度。如果模型为多分支模型,不同的分支处理速度是不一样的,所以处理快的模块需要等待其他模块运算完后再进行后续的处理,这个时候就存在算力的浪费。 -
更加灵活
多分支模型,需要各个分支的输出保持一致才能进行特征的相加,因此在对模型的修改上有一定的限制。同时,对于模型的剪枝工作而言,多分支网络普遍会存在性能大幅下降的问题。
结构重参数化
结构重参数化过程如下:
- 模型有三个分支,分别为 3×3 Conv + BN, 1×1 Conv + BN, BN,注意,因为有BN层的存在,所以这里的卷积层都不需要bias。
- 结构重参数化第一步,将三个分支都变为3×3 Conv.
- 将3个 3×3 Conv 合并成1个 3×3 Conv.
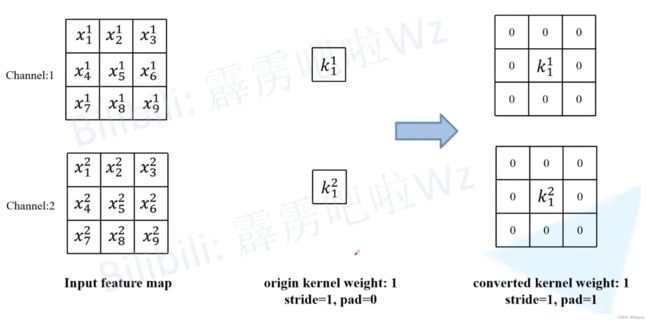
1×1 Conv 转变成 3×3 Conv
对 1×1 Conv 进行值为0的padding。同时,在转变后进行卷积操作就需要对输入特征进行padding,从而使得输入输出的特征图大小保持一致。
Identity 连接转变成 3×3 Conv:
构建的卷积操作,使得输入输出的特征层不仅大小一致并且特征值也保持一致。
Conv2d 和 BN 融合
Batch Normalization的计算公式如下:
y i = x i − μ i σ i 2 + ϵ ⋅ γ i + β i y_{i}=\frac{x_{i}-\mu_{i}}{\sqrt{\sigma_{i}^{2}+\epsilon}} \cdot \gamma_{i}+\beta_{i} yi=σi2+ϵxi−μi⋅γi+βi
RepVGG 给出的 Conv2d 和 BN融合的推导如下, M M M 为输入。
bn ( M , μ , σ , γ , β ) : , i , : , : = ( M : , i , : , : − μ i ) γ i σ i + β i W i , : , : , : ′ = γ i σ i W i , : , : , : , b i ′ = − μ i γ i σ i + β i bn ( M ∗ W , μ , σ , γ , β ) : , i , : , : = ( M ∗ W ′ ) : , i , : , : + b i ′ \begin{aligned} \operatorname{bn}(\mathrm{M}, \boldsymbol{\mu}, \boldsymbol{\sigma}, \boldsymbol{\gamma}, \boldsymbol{\beta})_{:, i, :,:}=\left(\mathrm{M}_{:, i, :,:}-\boldsymbol{\mu}_{i}\right) \frac{\boldsymbol{\gamma}_{i}}{\boldsymbol{\sigma}_{i}}+\boldsymbol{\beta}_{i} \\ \mathrm{W}_{i,:,:,:}^{\prime}=\frac{\boldsymbol{\gamma}_{i}}{\boldsymbol{\sigma}_{i}} \mathrm{~W}_{i,:,:,:}, \quad \mathbf{b}_{i}^{\prime}=-\frac{\boldsymbol{\mu}_{i} \gamma_{i}}{\boldsymbol{\sigma}_{i}}+\boldsymbol{\beta}_{i}\\ \operatorname{bn}(\mathrm{M} * \mathrm{~W}, \boldsymbol{\mu}, \boldsymbol{\sigma}, \boldsymbol{\gamma}, \boldsymbol{\beta})_{:, i, :,:}=\left(\mathrm{M} * \mathrm{~W}^{\prime}\right)_{:, i, :,:}+\mathbf{b}_{i}^{\prime} \end{aligned} bn(M,μ,σ,γ,β):,i,:,:=(M:,i,:,:−μi)σiγi+βiWi,:,:,:′=σiγi Wi,:,:,:,bi′=−σiμiγi+βibn(M∗ W,μ,σ,γ,β):,i,:,:=(M∗ W′):,i,:,:+bi′
Conv2d 和 BN 的融合后,相当于一个Conv2d。
多分支融合
O p t = ( I p t ⨂ W 1 + B 1 ) + ( I p t ⨂ W 2 + B 2 ) + ( I p t ⨂ W 3 + B 3 ) = I p t ⨂ ( W 1 + W 2 + W 3 ) + ( B 1 + B 2 + B 3 ) \begin{aligned} Opt &= (Ipt \bigotimes W_1 + B_1) + (Ipt \bigotimes W_2 + B_2) + (Ipt \bigotimes W_3 + B_3) \\ &= Ipt \bigotimes (W_1 + W_2 + W_3) + (B_1 + B_2+ B_3) \end{aligned} Opt=(Ipt⨂W1+B1)+(Ipt⨂W2+B2)+(Ipt⨂W3+B3)=Ipt⨂(W1+W2+W3)+(B1+B2+B3)