深度学习——学习笔记三

卷积神经网络

1.1计算机视觉           

        识别一张图片时，不一定只要识别出相应的物体，比如无人驾驶技术。在目标检测项目中，首先需要计算出图中有哪些物体，再将它们模拟成一个个盒子，或者用其他的技术，识别出他们在图片中的位置。

        另一个例子，是神经网络实现的图片风格迁移。你有一张图片（左），你想将他转换成右边的风格：

        

你有一张满意的图片和一张风格的图片，你可以用神经网络将他们融合在一起：

最后生成的图片是左边的轮廓和右边的风格。

应用风格迁移时，需要注意的一点是数据的输入可能会非常大。之前64*64的图片，其实是64*64*3=12288的维度，如果你要操作1000*1000的图片，维度是3M，你也许会有1000个隐藏单元 ，而所有的权值，组成了矩阵W^[1],这个矩阵的大小，将会是3M*1000，这意味着矩阵w^[1]会有30亿个参数！

1.2边缘检测示例

        卷积运算是卷积神经网络的重要组成部分，使用边缘检测作为入门样例。

        前面提到深层需要做的是检测物体的一个部分，或检测整个物体。那么怎么检测一个边缘呢？

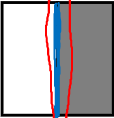
        以这个图片为例，我们首先检测的是他的垂直边缘，人的身体和直栏便被检测出来；然后检测水平边缘，横槛就被检测到了。如何检测的呢？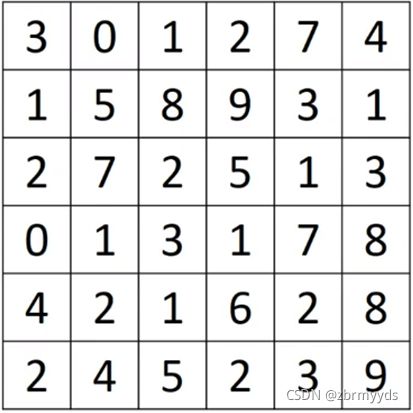 

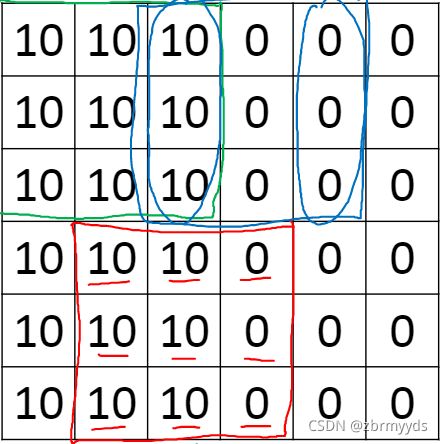
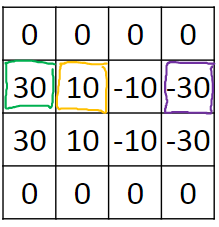
        这是一个6*6的灰度图像，也就是6*6*1的矩阵A，为了检测边缘，我们可以创建一个3*3的过滤器filter，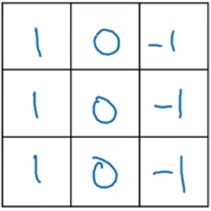 

 在论文中，有时会叫他kernel（核），对他们做卷积运算，用A*filter表示，*是卷积运算的标准符号，得到的结果是4*4*1的矩阵，可以看成是一个4*4的图像。将过滤器覆盖在矩阵的第一个3*3方阵，如图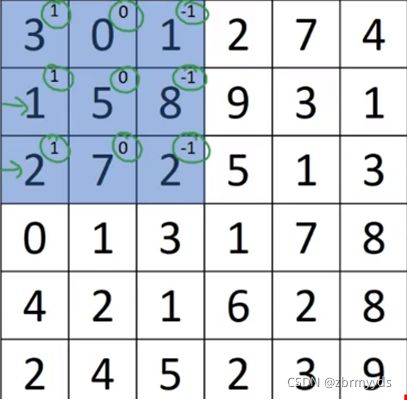

 4*4矩阵的第一个结果是每个方格元素之积的和，即3*1+0*0+1*-1+1*1+5*0+8*-1+2*1+7*0+2*-1=-5。第二个元素就是从左到右第二个方阵，依次计算。如果要用代码编程计算实现，需要用到conv-forward函数。

         上边这个图像，要检测他的边缘，先将他的像素矩阵直观写出来。

而一个过滤器是这样的： 

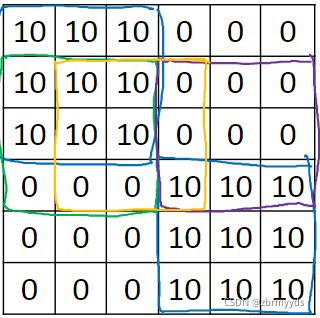
我们可以清晰地知道10和0之间是边缘，用这两个矩阵进行卷积运算，就得到了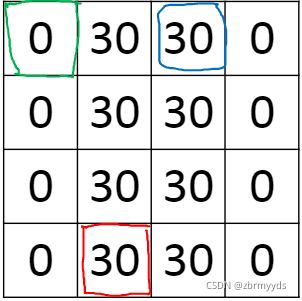 

这样一个图像，将边缘位置用像素表示了出来。最终结果有点太粗了 

但如果图片增大到1000*1000，最终结果会很好的展现出来。

1.3更多边缘检测内容 

         见过了垂直滤波器，水平滤波器一目了然。

         用它来检测如图矩阵

得到的结果为 

        此外，还有许多滤波器 

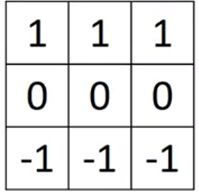
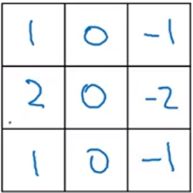
这是sobel滤波器，它的优势在于增加了中间一行的权重，使结果的rubust（稳定性）提高了 。

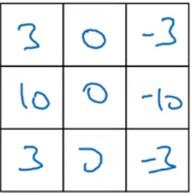
这是Scharr滤波器。但在处理图像的过程中，你不一定需要使用科学家们研究出来的方法，你可以把滤波器的9个元素当作9个参数，用反向传播方法去实现。这种参数矩阵能够检测出45度或者70度，甚至是任何角度的边缘。不过构成这些计算的基础，依然是卷积运算，使得神经网络能够学习任何他所需的3*3滤波器，并应用到整张图片中。

1.4padding

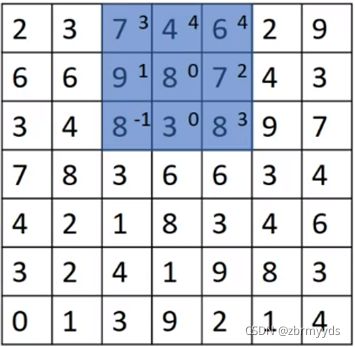
         padding是一个基本的卷积操作。对于一个n*n的矩阵和一个f*f的过滤器，对他们进行卷积运算，得到的是（n-f+1）*（n-f+1）的矩阵，但有2个缺点，1个就是图像会越来越小，最后变得没有意义；第二个就是如果你注意角落边的像素，就会有许多3*3的区域与之重叠，所以在输出中采用较少，意味着你丢掉了图像边缘位置的许多信息。为了解决以上问题，你可以在卷积操作之前，填充这幅要处理的图像，你可以沿着图像边缘再填充一层像素，这样6*6的矩阵就可以变成8*8的矩阵，经过卷积，你就可以得到6*6的矩阵，大小没有发生变化。习惯上，我们会填充0，p是填充的数量，此时p=1，输出就变成了（n+2p-f+1）*（n+2p-f+1），此时的边缘或角落信息发挥作用也会变小，这一缺点也被削弱了。

        至于选择填充多少像素，通常有两个选择，叫做Valid卷积和Same卷积。

        Valid卷积：不填充像素，得到（n-f+1）*(n-f+1)。

        Same卷积：填充p个像素，使得输入与输出矩阵维度相同，即（n+2p-f+1）=n

 所以p=（f-1）/2，如果f是奇数，那么结果就是正常的输出，而习惯上通常f就是奇数，第一个是因为如果f是偶数，那么Same就无法做到自然填充；第二个，如果你是一个奇数维过滤器，他就有一个中心点，方便指出过滤器的位置。

1.5卷积步长        

         

 一个7*7的矩阵和一个3*3的过滤器，不同的是步幅改为了2，我们会让过滤器跳过2个步长，最终得到3*3的矩阵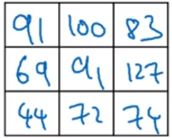

 对于一个n*n矩阵和一个f*f过滤器，padding为p，步幅为s，最终得到

（（n+2p-f）/s+1）*（（n+2p-f）/s+1）的矩阵，如果结果不是整数，我们将括号里的数看作一个整体z，对z向下取整[z]。当然如果步幅过大，过滤器不能超过矩阵边缘，必须完全处于图像之中。

 1.6卷积为何有效

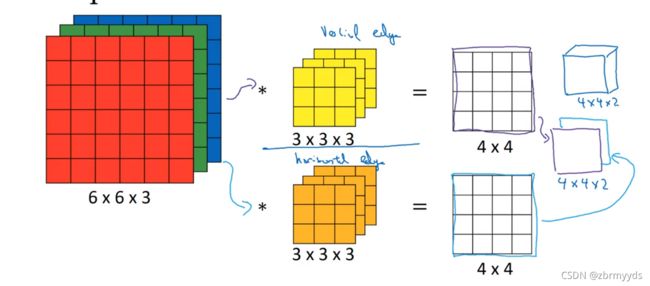
         假如不是灰度图像，而是RGB的彩色图像，假设他为6*6*3，高为6，宽为6，通道的数目为3。则过滤器也应有三层，他们的输出是一个4*4*1的图像。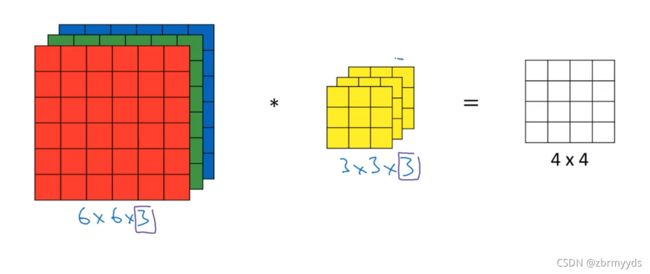

        为了简化，将他们看作三维的长方体和立方体，将立方体放入长方体的第一个3*3*3的区域中，对这27组数分别的积求和，即为4*4矩阵的第一个结果。

        如果你仅仅想求出红色通道的边缘，则只需过滤器与红色通道对应的通道为之前的过滤器，其他两层各个元素均为0。如果有多个过滤器：

     

则将2次的输出结果堆叠成一个4*4*2的矩阵，看作一个小长方体 。

1.7单层卷积网络

         

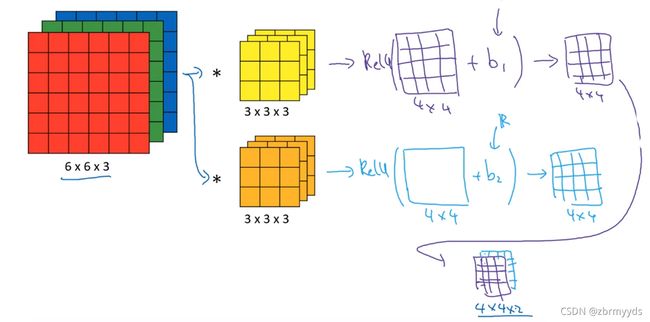
将之前得到的结果加上误差b1，b2，再加上非线性函数ReLU ，说明它是一个非线性激活函数。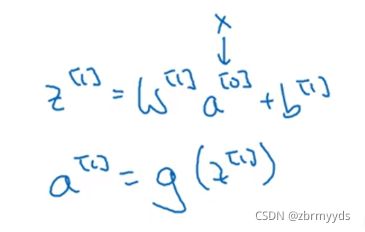

这是前向传播的一个操作，a[0]就是输入的图像，过滤器用变量w^[1]来表示，卷积的结果为w^[1]*a^[0],加上的误差就是b^[1] 。

        无论输入的照片有多大，它的参数始终有过滤器的维度*数量决定，这就是卷积神经网络的一个特征，叫做“避免过拟合”。

        现在用f^[l]=f，表示l层中过滤器的大小为f*f，p^[l]=padding，padding数量既可以指定为Valid卷积，也就是padding=0，也可以指定为Same卷积，使得输入输出图片高度和宽度相同。用s^[l]标记步幅。这一层的输入记为nH^[l-1]*nW^[l-1]*nC^[l-1],nC是通道的数量，l-1表示这是上一层的激活值。将上标改为l，就是这一层的输出值，用如图来表示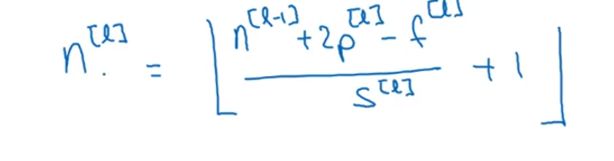

 加上下标nH^[l]可以算出输出层的高度，同理可得宽度。

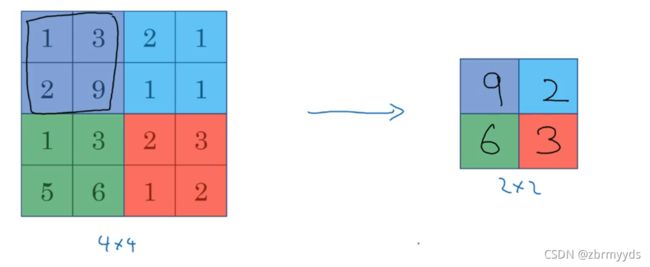
1.9池化层

                

        把左边矩阵分成四大块，每块取最大值得到右边的矩阵 。我们需对2*2的区域进行计算，好像应用了一个2*2的过滤器，步幅为2，这些就是最大池化的超级参数f=2，s=2。

        最大化运算的实际作用是，如果在过滤器中提取到某个特征，那么保留其最大值，如果没有，则该特征不存在。人们使用最大池化的原因就是他在许多实验中效果都很好。

         如果矩阵是三维的，那么输出结果也是三维。

        还有另外一种池化方法——平均池化，就是把对应的区域取平均值。

1.11为什么使用卷积？

        

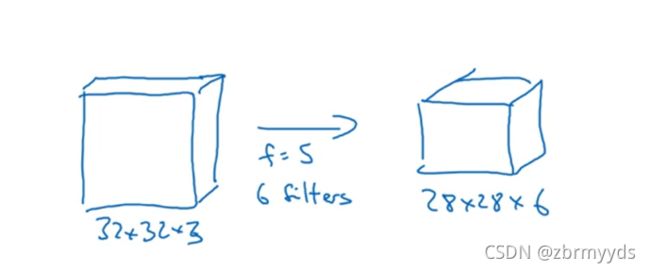
        如图对图像卷积操作，原矩阵为32*32*3=3072，新矩阵为28*28*6=4704 。两层中的每个神经元彼此相连，然后计算权重矩阵，等于3072*4704~~14M，过滤器有6个，5阶，再加上偏差参数，为（5*5+1）*6=156个。

        卷积网络映射参数这么少是有原因的：一种方法是参数共享，观察发现，特征检测如垂直边缘检测如果应用于图片的某一区域，那么它也可能适用于图片的其他区域，他不仅适用于低阶特征，同样适用于高阶，例如提取脸上的眼睛。即使减少参数，9个参数依然能计算出16个输出；第二种方法是使用稀疏连接，对于输出值，它只与3*3的输入特征有关联，其他像素值都不会使他的输出值变化，以便于我们用最小的训练集来训练他，从而预防过度拟合。

        神经网络善于捕捉平移不变，因为即使移动几个像素，这张图片依然具有非常相似的特征。

        最后，我们将这些层整合起来，看如何训练这些网络：

输入图片，添加卷积层和池化层，然后添加全连接层，最后输出softmax，即“y帽” ，成本函数：

        所以训练神经网络，你要做的就是使用梯度下降法 ，或其他算法，例如含冲量的梯度下降，

含RMSProp或其他因子的梯度下降，来优化神经网络中的所有参数，以减少代价函数J的值。