【深度学习-笔记】(2)--高斯过程&高斯回归
【深度学习-笔记】(2)–高斯过程&高斯回归
个人笔记,记录思考过程,已注明参考文献。
如果你看不懂他,可以试着先去接受他。就好像,打不过就加入。
文章目录
- 【深度学习-笔记】(2)--高斯过程&高斯回归
-
- 一、高斯分布(正态分布)
- 1. 一元高斯分布
- 2. 多元(二元及以上)高斯分布
- 二、高斯过程
- 三、高斯过程回归(Gauss Process Regression,GPR)(待更新)
- 参考文献
一、高斯分布(正态分布)
高斯分布(正态分布)是一个常见的连续概率分布。
正态分布的数学期望值或期望值 μ μ μ等于位置参数,决定了分布的位置;其方差 σ 2 \sigma^{2} σ2的开平方或标准差σ等于尺度参数,决定了分布的幅度。正态分布的概率密度函数曲线呈钟形,因此人们又经常称之为钟形曲线(类似于寺庙里的大钟,因此得名)。
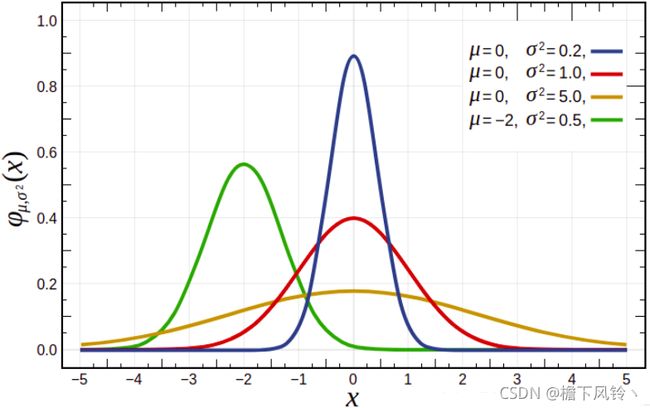
我们通常所说的标准正态分布是位置参数 μ = 0 \mu=0 μ=0,方差 σ 2 = 1 \sigma^{2}=1 σ2=1的正态分布。
1. 一元高斯分布
若随机变量X服从一个位置参数为 μ μ μ,方差为 σ 2 σ^{2} σ2的正态分布,可以记为 X X X~ N ( μ , σ 2 ) N ( μ , σ^{2} ) N(μ,σ2),则其概率密度函数为:
f ( x ) = 1 σ 2 π exp ( − ( x − μ ) 2 2 σ 2 ) f(x)=\frac{1}{\sigma \sqrt{2 \pi}} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right) f(x)=σ2π1exp(−2σ2(x−μ)2)
其中, μ \mu μ和 σ 2 \sigma^{2} σ2的求法不再赘述。
2. 多元(二元及以上)高斯分布
这里以二元高斯分布为例: 二维高斯分布则包含有两个变量,二维高斯分布的均值 μ μ μ由两个变量的均值描述,其方差由变量的协方差矩阵进行描述,协方差矩阵 Σ \Sigma Σ表示的是两个变量之间的关系(标准差和方差一般是用来描述一维数据的,而面对二维数据,则使用协方差来表示):
μ = ( μ a μ b ) Σ = ( σ x 2 ρ σ x σ y ρ σ x σ y σ y 2 ) \mu=\left(\begin{array}{l} \mu_{a} \\ \mu_{b} \end{array}\right) \quad \Sigma=\left(\begin{array}{cc} \sigma_{x}^{2} & \rho \sigma_{x} \sigma_{y} \\ \rho \sigma_{x} \sigma_{y} & \sigma_{y}^{2} \end{array}\right) μ=(μaμb)Σ=(σx2ρσxσyρσxσyσy2)
其中, ρ σ x σ y \rho \sigma_{x} \sigma_{y} ρσxσy和 ρ σ x σ y \rho \sigma_{x} \sigma_{y} ρσxσy分别为两个变量的协方差值。协方差的计算公式为:
Cov ( X , Y ) = E [ ( X − E ( X ) ( Y − E ( Y ) ] = E [ X Y ] − E [ X ] E [ Y ] \begin{aligned} \operatorname{Cov}(X, Y) &=E[(X-E(X)(Y-E(Y)]\\ &=E[X Y]-E[X] E[Y] \end{aligned} Cov(X,Y)=E[(X−E(X)(Y−E(Y)]=E[XY]−E[X]E[Y]
其中,若为一维数据,协方差可以表示为:
cov ( X ) = ∑ i = 1 n ( X i − X ˉ ) ( X i − X ˉ ) n − 1 = ∑ i = 1 n ( X i − X ˉ ) 2 n − 1 \operatorname{cov}(X)=\frac{\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)\left(X_{i}-\bar{X}\right)}{n-1}= \frac{\sum_{i=1}^{n}{\left(X_{i}-\bar{X}\right)}^{2}}{n-1} cov(X)=n−1∑i=1n(Xi−Xˉ)(Xi−Xˉ)=n−1∑i=1n(Xi−Xˉ)2
其实就是方差公式。而对于多维数据,为度量各个维度偏离其均值的程度,协方差可以表示为:
Σ = cov ( X , Y ) = ∑ i = 1 n ( X i − X ˉ ) ( Y i − Y ˉ ) n − 1 \Sigma=\operatorname{cov}(X,Y)=\frac{\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{n-1} Σ=cov(X,Y)=n−1∑i=1n(Xi−Xˉ)(Yi−Yˉ)
这里Σ是对称正定的n × n矩阵。具体计算可参考协方差计算。最后,二元高斯随机变量 x x x~ N ( μ , Σ ) N ( μ , \Sigma ) N(μ,Σ),其概率密度可以表示为:
P ( x ; μ , Σ ) = 1 ( 2 π ) n / 2 ∣ Σ ∣ 1 / 2 exp ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) P(x; μ , \Sigma)=\frac{1}{{(2 \pi)}^{n/2} {|\Sigma|}^{1/2}} \exp \left(-\frac{1}{2}(x-\mu)^{T} \Sigma^{-1}(x-\mu)\right) P(x;μ,Σ)=(2π)n/2∣Σ∣1/21exp(−21(x−μ)TΣ−1(x−μ))
其中
x = [ x A x B ] μ = [ μ A μ B ] Σ = [ Σ A A Σ A B Σ B A Σ B B ] 。 x=\left[\begin{array}{l} x_{A} \\ x_{B} \end{array}\right] \quad \mu=\left[\begin{array}{l} \mu_{A} \\ \mu_{B} \end{array}\right] \quad \Sigma=\left[\begin{array}{ll} \Sigma_{A A} & \Sigma_{A B} \\ \Sigma_{B A} & \Sigma_{B B} \end{array}\right]。 x=[xAxB]μ=[μAμB]Σ=[ΣAAΣBAΣABΣBB]。
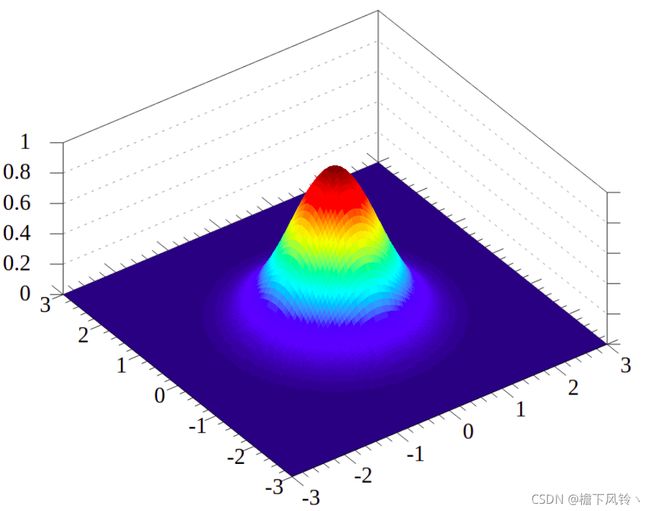
二、高斯过程
高斯过程是指随机变量的一个集合,其中任意有限个样本的线性组合都有一个联合高斯分布。
一个高斯过程是由均值函数 m ( x ) m(x) m(x)和协方差函数 k ( x , x ∗ ) k(x,x^{*}) k(x,x∗)确定的。它可理解成高斯分布的一个生成过程。高斯分布的均值和协方差是向量和矩阵(意思就是多维高斯分布的均值和方差是确定的值,比如均值是(0.1,0.2,0.5)。),而高斯过程的均值和方差则分别是均值函数和协方差矩阵函数。
1.有限域
设 X = X= X= { x 1 , . . . , x m {x}_{1},...,{x}_{m} x1,...,xm}是任意有限集(定义域有限),考虑所有可能的 f : X → R f:X→R f:X→R所组成的函数集合 H H H,那么得到的 f f f也是有限的,用集合来表示:
f ⃗ = [ f ( x 1 ) f ( x 2 ) ⋯ f ( x m ) ] T \vec{f}=\left[\begin{array}{llll} f\left(x_{1}\right) & f\left(x_{2}\right) & \cdots & f\left(x_{m}\right) \end{array}\right]^{T} f=[f(x1)f(x2)⋯f(xm)]T
那么有限域的高斯过程为:
f ⃗ ∼ N ( μ ⃗ , σ 2 I ) \vec{f} \sim \mathcal{N}\left(\vec{\mu}, \sigma^{2} I\right) f∼N(μ,σ2I)
其中, I I I为单位矩阵。 μ ⃗ = E ( f ( x ) ) \vec{\mu}=E(f(x)) μ=E(f(x))
表达式为:
p ( h ) = ∏ i = 1 m 1 2 π σ exp ( − 1 2 σ 2 ( f ( x i ) − μ i ) 2 ) p(h)=\prod_{i=1}^{m} \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{1}{2 \sigma^{2}}\left(f\left(x_{i}\right)-\mu_{i}\right)^{2}\right) p(h)=i=1∏m2πσ1exp(−2σ21(f(xi)−μi)2)
2.无限域
无限域体现在由 X X X组成的集合中, x x x是随机的,有无限多的组合。假设有一个随机变量的集合:{ f ( x ) : x ∈ X f(x):x \in X f(x):x∈X},这里定义高斯过程是一个随机过程,满足随机变量集合的任意有限子集都服从多元高斯分布。那么设定均值函数 m ( x ) m(x) m(x)和协方差函数 k ( x 1 , x 2 ) k({x}_{1},{x}_{2}) k(x1,x2)。
如果随机变量集合: f ( x ) : x ∈ X f(x):x \in X f(x):x∈X是从均值函数为 m m m、协方差函数为 k k k的高斯过程中取出的变量集,那么对于任意有限集合: x 1 , . . . , x m ∈ X {x}_{1},...,{x}_{m} \in X x1,...,xm∈X,它们相对应的随机变量 f ( x i ) f(x_i) f(xi)服从高斯分布:
[ f ( x 1 ) ⋮ f ( x m ) ] ∼ N ( [ m ( x 1 ) ⋮ m ( x m ) ] , [ k ( x 1 , x 1 ) ⋯ k ( x 1 , x m ) ⋮ ⋱ ⋮ k ( x m , x 1 ) ⋯ k ( x m , x m ) ] ) \left[\begin{array}{c} f\left(x_{1}\right) \\ \vdots \\ f\left(x_{m}\right) \end{array}\right] \sim \mathcal{N}\left(\left[\begin{array}{c} m\left(x_{1}\right) \\ \vdots \\ m\left(x_{m}\right) \end{array}\right],\left[\begin{array}{ccc} k\left(x_{1}, x_{1}\right) & \cdots & k\left(x_{1}, x_{m}\right) \\ \vdots & \ddots & \vdots \\ k\left(x_{m}, x_{1}\right) & \cdots & k\left( x_{m},{x}_{m}\right) \end{array}\right]\right) ⎣ ⎡f(x1)⋮f(xm)⎦ ⎤∼N⎝ ⎛⎣ ⎡m(x1)⋮m(xm)⎦ ⎤,⎣ ⎡k(x1,x1)⋮k(xm,x1)⋯⋱⋯k(x1,xm)⋮k(xm,xm)⎦ ⎤⎠ ⎞
记为:
f ( x ) ∼ G P ( m ( x ) , k ( x , x ′ ) ) f(x)\sim{GP}(m(x),k(x,x')) f(x)∼GP(m(x),k(x,x′))
其中,均值和协方差记为:
m ( x ) = E [ x ] k ( x , x ′ ) = E [ ( x − m ( x ) ) ( x ′ − m ( x ′ ) ) ] m(x)=E[x] \\ k(x,x')=E[(x-m(x))(x'-m(x'))] m(x)=E[x]k(x,x′)=E[(x−m(x))(x′−m(x′))]
☆☆☆扩展矩阵的协方差:(待更新)。
三、高斯过程回归(Gauss Process Regression,GPR)(待更新)
设 L L L为训练集,训练数据独立同分布,分布未知,我们定义高斯过程回归模型(Gaussian Process Regression,以下简称GPR)的表达式为:
高斯核: k ( X , X ∗ ) = σ 2 exp ( − ∥ X − X ∗ ∥ 2 2 l 2 ) k\left(X, X^{*}\right)=\sigma^{2} \exp \left(-\frac{\left\|X-X^{*}\right\|^{2}}{2 l^{2}}\right) k(X,X∗)=σ2exp(−2l2∥X−X∗∥2)
其中 σ \sigma σ和 l l l为超参数。
参考文献
高斯分布
如何通俗易懂地介绍 Gaussian Process?
高斯过程和高斯过程回归
高斯过程回归(Gaussian Process Regression)
多元高斯分布(The Multivariate normal distribution)
【吴恩达】斯坦福AI大牛带你吃透机器学习!
机器学习中的高斯过程
图文详解高斯过程(一)——含代码
高斯过程 Gaussian Processes 原理、可视化及代码实现
1.7. 高斯过程(Gaussian Processes)