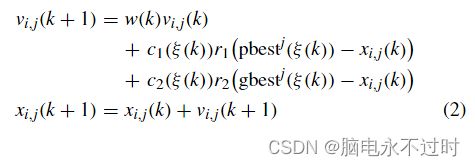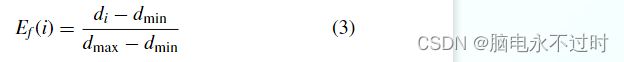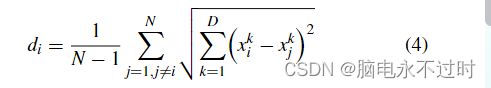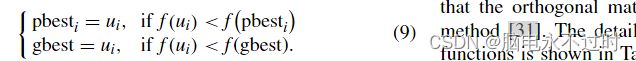基于动态邻域的切换粒子群优化算法

英文: A Dynamic Neighborhood-Based Switching Particle Swarm Optimization Algorithm

摘要：

本文提出了一种基于动态邻域的切换PSO（DNSPSO）算法，该算法设计了一种新的速度更新机制，根据基于距离的动态邻域调整个人最佳位置和全局最佳位置，以充分利用整个群体中的种群进化信息。此外，引入了一种新的切换学习策略，以自适应地选择加速度系数并根据每次迭代时的搜索状态更新速度模型，从而有助于彻底搜索问题空间。此外，将差分进化算法与粒子群优化（PSO）算法成功地混合，以缓解过早收敛的问题。利用一系列常用的基准函数（包括单峰、多峰和旋转多峰情况）来综合评估DNSPSO算法的性能。实验结果表明，所开发的DNSPSO算法在求解精度和收敛性能方面优于许多现有的PSO算法，尤其是对于复杂的多模态优化问题。

引文:

过去几十年，由于优化技术在各个研究领域具有明显的应用潜力，包括医疗保健、工程和电信[19]、[22]、[24]、[36]、[40]，优化技术得到了快速发展。作为一个强大的优化技术家族，进化计算（EC）方法在解决优化问题方面表现出了突出的性能。一些流行的EC方法包括遗传算法、禁忌搜索、模拟退火、粒子群优化（PSO）等[19]、[21]、[24]、[25]、[44]。与其他EC算法相比，[15]中提出的PSO算法由于其易于实现、快速收敛速度、保证分集和令人满意的精度，表现出竞争性甚至优越的性能。

受模仿社会行为（例如鸟类成群和鱼类成群）的启发，粒子群算法通过基于群体智能更新粒子的速度和位置来探索问题空间。事实上，粒子群优化算法由于其有效搜索全局最优解的强大能力而成为一种有吸引力的优化技术。在这方面，PSO算法已被广泛研究并成功应用于各个研究领域[4]、[13]、[27]、[48]、[49]。然而，已经发现，当存在大量局部最优时，PSO算法存在过早收敛和收敛性能差的某些缺点，尤其是在高维优化问题中[18]，[26]，[29]。因此，近年来，人们做出了巨大努力来开发可分为四种类型的变型PSO算法：1）修改参数[6]、[30]、[33]、[34]、[38]；2） 与其他EC算法杂交[14]，[32]，[42]，[45]；3） 使用拓扑进行速度更新[2]，[16]–[18]，[26]，[29]；以及4）引入控制理论来设计新的学习策略。

最近，开发具有不同拓扑和学习策略的PSO算法已成为研究热点[3]。通常，这些类型的PSO变体旨在增强PSO算法的种群多样性并缓解过早收敛问题。特别是，[16]中讨论了五种众所周知的拓扑结构（包括全、环、簇、金字塔和冯·诺依曼）。[26]中引入了一种完全知情的PSO算法，其中每个粒子的速度根据其邻居的信息进行更新。在[18]中，开发了一种综合学习PSO算法，其中通过从不同粒子的局部最佳位置学习来更新单个粒子的每个维度。此外，[29]中提出了一种局部知情的PSO算法，其中粒子被引导通过在邻域中选择的几个个人最佳位置来探索问题空间。

采用上述拓扑的所开发的PSO变体在搜索全局最优解方面表现出令人满意的性能。尽管如此，这些PSO变体的拓扑结构在初始化阶段确定，并在进化过程中保持不变，这表明粒子的邻域是固定的。在这种情况下，具有固定邻域的PSO算法具有以下两个局限性：1）很难为大多数优化问题寻求理想拓扑；2）固定邻域可能导致局部搜索性能不佳。

为了解决上述问题，本文提出了一种基于距离的动态邻域，以更新个人最佳位置pbest和全局最佳位置gbest，从而增强逃离局部最优的能力。传统的粒子群算法仅基于整个群发现的pbest和gbest信息来更新每个粒子的速度和位置。也就是说，传统PSO算法的搜索策略将社会学习部分限制在可能导致过早收敛问题的gbest上。此外，不能保证gbest总是接近全局最优，特别是对于具有大量局部最优解的复杂优化问题。为了充分利用其他粒子的邻域信息，本文基于发展的动态邻域，提出了一种新的pbest和gbest更新机制。请注意，群体的进化过程可以分为四种搜索状态，包括收敛、探索、开发和跳出[46]（convergence, exploration, exploitation, and jumping out）。为了进一步增强PSO算法的搜索能力，引入了一种新的切换学习策略，以自适应地选择加速度系数，并根据每次迭代时由进化因子确定的搜索状态调整速度更新模型。此外，差分进化（DE）算法[45]用于进一步增强pbest和gbest的多样性。

基于以上讨论，我们的目标是提出一种基于动态邻域的切换PSO（dynamic neighborhood-based switching PS）（DNSPSO）算法，以提高PSO算法的搜索性能。本研究的主要贡献总结如下：

1） 提出了一种DNSPSO算法，其中提出了一个基于距离的动态邻域，通过根据其对应的邻域更新pbest和gbest来充分利用邻域信息，这有助于很高的概率逃离局部最优。
2） 设计了一种切换学习策略，其中在每次迭代时自适应调整加速度系数，并根据进化因子确定的搜索状态调整速度更新模型。

3） 在14个著名的基准函数（包括单峰、多峰和旋转多峰情况）上对DNSPSO算法的性能进行了综合评估，实验结果表明，所提出的DNSPSO算法在收敛性能和解质量方面优于一些现有的PSO算法，特别是对于复杂的多模态优化问题。

本文的其余部分组织如下。在第二节中，介绍了传统的PSO算法和PSO变体。第三节介绍了基于距离的动态邻域和提出的DNSPSO算法。第四节讨论了参数设置、基准函数和实验结果。最后，第5节给出了结论和未来的工作.

二、pso算法

A、 传统PSO算法

PSO算法是一种基于种群的EC方法，其中每个粒子的位置用作优化问题的潜在解决方案[15]。在PSO算法[15]中，每个粒子通过学习其经验并与其他粒子合作来搜索问题空间。

在D维问题空间中，第i个粒子在第k次迭代时的位置表示为x i（k）=（x i 1（k），x i 2（k）…，x iD（k））。第k次迭代时粒子i的速度由v i（k）=（v i 1（k），v i 2（k）…，v iD（k））表示。更新粒子i的速度和位置的规则描述如下：

其中p i和p g表示粒子i和整个群找到的最佳解，称为pbest和gbest；w是惯性权重，它是控制先前速度对当前速度影响的比例因子；r1和r2是从[0，1]中采样的两个均匀分布的随机数；c1和c2分别是将粒子推向pbest和gbest的认知加速系数和社会加速系数。

B.PSO变体

近年来，为了提高传统粒子群算法的搜索能力，人们开发了大量的变异粒子群算法。已经引入了各种参数更新策略，通过调整参数（例如，惯性权重、认知加速系数和社会加速系数）来提高PSO算法的性能[33]。通常，较大的惯性权重有助于全局搜索，较小的惯性权重将有利于局部细化。[34]中提出了一种线性减小惯性权重的PSO（PSO-LDIW）算法，以提高PSO算法的搜索能力。[30]中提出了一种具有时变加速度系数的PSO算法，旨在有效控制局部和全局探索。在[6]中，为了提高收敛速度和搜索能力，在PSO算法（PSO-CK）中引入了收缩因子。特别是，在[38]中提出的切换PSO（SPSO）算法中使用了马尔可夫链来自适应地控制惯性权重和加速度系数。

一些变型PSO算法侧重于设计新的拓扑结构，以保证种群多样性和防止过早收敛。PSO算法中引入了几种流行的拓扑结构（包括全、环、簇、金字塔和冯·诺依曼）[16]。通过充分利用邻域信息，[26]中开发了一种完全知情的PSO算法。在综合学习PSO算法中，提出了一种新的学习策略，通过利用所有其他粒子的个体最佳信息来更新每个粒子[18]。此外，[29]中引入了一种局部知情的PSO算法，通过使用邻域中的几个局部最佳位置来指导粒子的搜索。

设计新PSO算法的另一个研究方向是与其他EC算法混合。已经发现，PSO算法和其他EC方法的组合在提高PSO算法的性能方面显示出了希望[45]。此外，人们对将社会学/生物学启发的方法引入PSO算法越来越感兴趣，例如小生境PSO算法[5]、老化理论启发的PSO算法7]、基于文化的PSO方法[8]等。

最近，复杂系统和控制理论已被应用于PSO算法，如混沌、模糊、神经网络、时延和正交学习[10]、[20]、[28]、[35]、[47]。作为一个显著的例子，粒子的延迟信息已被用于切换延迟PSO（SDPSO）算法中，以充分利用进化过程的历史信息，从而有助于比传统PSO算法更好地探索问题空间。

三、 基于动态邻域的切换PSO算法

在本节中，主要从三个方面讨论了所提出的DNSPSO算法：1）引入基于距离的动态邻域，基于其对应的邻域来调整pbest和gbest，这有利于深入探索问题空间，从而缓解过早收敛问题；2） 利用所开发的切换策略自适应地选择加速度系数并根据搜索状态更新速度；3）采用DE方法来增强PSO算法的多样性。因此，所提出的DNSPSO算法可以彻底搜索问题空间，以便有效地发现最优解。

A、 DNSPSO算法框架

在所提出的DNSPSO算法中，粒子i在迭代k处的速度和位置由以下机制更新：

其中r1和r2是分布在[0,1]中的两个随机数；j表示问题空间的维数；c1（ξ（k））和c2（ξ（k））分别是认知加速系数和社会加速系数。

请注意，c1（ξ（k））、c2（ξ（k））、pbest和gbest根据模式相关马尔可夫链ξ（k）（k>0）定义，由概率转移矩阵P=（P ij）J×J确定的马尔可夫链在有限状态空间中取一个值：F={1，2，…，J}，其中pij≥ 0（i，j）∈F）和∑ pij=1。在本文中，ξ（k）表示四种不同的搜索状态（J=4）。

特别地，每个粒子的当前搜索状态由概率转移矩阵P和进化因子E f决定[46]。E f是描述群体分布特性的指标：

其中d max和d min分别表示d i之间的最大距离和最小距离。di是粒子i和其他粒子之间的平均距离，计算如下：

其中N和D分别表示群大小和问题空间的维度。

应该提到的是，（3）中定义的E f与[46]中定义的不同。具体而言，在本文中，（4）中定义了d i，这与[46]中的定义不同。搜索状态的分类规则和概率转移矩阵P如下所示：

B、基于距离的动态邻域

如前所述，传统的粒子群优化算法仅基于其单个pbest和整个群发现的gbest更新每个粒子。图1显示了传统PSO算法更新策略的缺点，其中黄色星表示gbest，黑色三角形表示局部最优，红色圆圈表示由白色圆圈表示的粒子的pbest，蓝色圆圈表示另一个粒子的pbst。需要指出的是，图1中的矢量相加满足平行四边形定律。由于加速度系数c1和c2以及随机数r1和r2的影响，一些分量的长度略有变化。根据（1），利用红圈和黄星来确定白色粒子的下一个位置。在这种情况下，移动轨迹是接近局部最优的红色虚线。请注意，如果红色圆圈替换为蓝色圆圈，结果会有很大不同。因此，我们可以得出结论，充分利用群的信息有助于缓解过早收敛问题，特别是对于具有大量局部最优解的测试函数。

为了解决这一缺点，本文引入了一个动态邻域来增强群中的通信，通过计算粒子的当前pbest和其他粒子之间的欧几里得距离，将粒子pi的邻域定义为最近的k个粒子。在进化过程中，每个粒子的邻域在每次迭代时都会自动调整。为了充分利用其他粒子的邻域信息，本文基于开发的动态邻域设计了一种新的pbest和gbest更新机制。在所提出的基于距离的动态邻域中，粒子pi从群中随机选择另一个粒子，并从所选粒子的pbest的邻居学习。此外，使用从当前全局最优解gbest的邻域中随机选择的粒子来更新粒子pi的速度，而不是当前gbest的速度。通过学习gbest的邻域，可以大大降低陷入局部最优的可能性。拟议学习策略的示意图如图2所示，其详细程序如下：

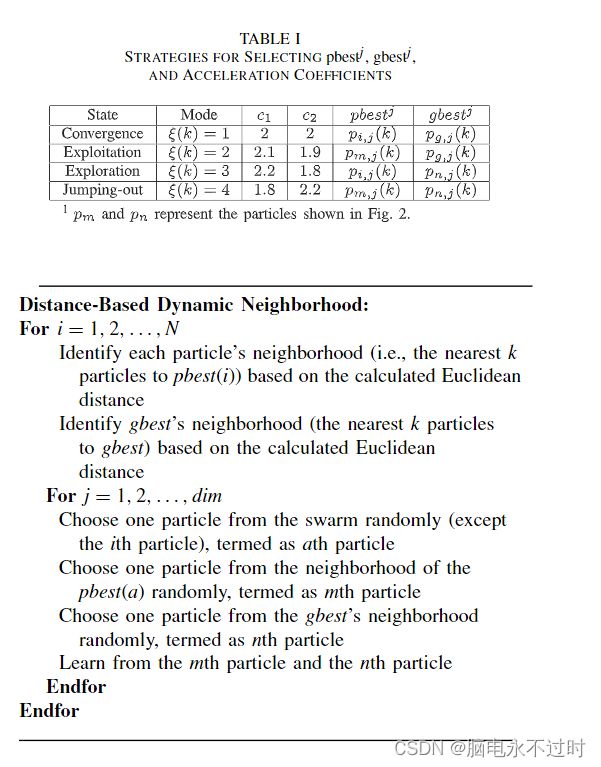
基于距离的动态邻域：

for i=1，2，…，N

         根据计算出的欧几里德距离确定每个粒子的邻域（即距离pbest（i）最近的k个粒子）

         基于计算的欧几里德距离确定gbest的邻域（与gbest最近的k个粒子）

         for j=1，2，…，dim

                从群中随机选择一个粒子（第i个粒子除外），称为第h个粒子

               从pbest（a）附近随机选择一个粒子，称为第m个粒子

               从gbest的邻域中随机选择一个粒子，称为第n个粒子

               学习第m个粒子和第n个粒子

         结束

结束

C、 切换学习策略

提出的DNSPSO算法的切换学习策略如表I所示。应该指出的是，c1和c2是在我们先前工作的基础上设置的[43]。同时，更多细节可以在[46]中找到，作者提出了选择C1和C2的策略

根据（2），c1的大值有利于个人搜索，而c2的小值减轻了gbest的影响。开发和探索状态的主要目的是彻底发现搜索空间，避免粒子陷入局部最优。在这种情况下，开采状态和勘探状态都具有较小的c2值和较大的c1值。在跳出状态下，采用较大的c2和较小的c1，其目的是将粒子推离当前的最佳位置

除了加速度系数c1和c2的值设置之外，以下提供四种搜索状态的更全面的描述。

1） 在收敛状态下，DNSPSO算法中的速度更新策略与传统PSO算法相同。也就是说，每个粒子都从自己的pbest和当前的gbest中学习。

2） 在开发状态下，鼓励粒子尽可能多地搜索问题空间，尤其是每个粒子的pbest周围的区域。对于粒子pi，我们首先从群中随机选择另一个粒子，然后从选定粒子的pbest的相邻粒子中随机选择一个称为pm的粒子。最后，我们将粒子pi的原始pbest替换为pm。通过这种方式，粒子在群中共享信息，这有利于粒子在整个问题空间中进行利用。

3） 在探索状态下，所有粒子都倾向于在发现的最优解区域周围搜索，以防止陷入局部最优。因此，我们在gbest的基于距离的动态邻域中随机选择一个称为pn的粒子来替换当前gbest。这样，DNSPSO算法中的群可以具有更宽的搜索区域，而不是拥挤在当前的gbest周围，成为局部最优的可能性很高。

4） 在跳出状态下，所有粒子都被驱动以逃离当前的局部最优，并发现更好的最优解。在这种情况下，我们同时调整开采和勘探阶段的pbest和gbest步骤，以便尽快找到更好的全局最优值。

此外，进化因子E f代表种群多样性。E f越大，多样性越差。惯性重量w由E f确定，如所示：

更详细的信息可参见[38]。

D、 差分进化算法（DE算法 Differential Evolution）

DE算法作为一种基于随机种群的进化算法，已被广泛研究以改进PSO算法的性能[42]，[45]。DE算法的混合不仅可以保证pbest和gbest的多样性，而且可以增强逃离局部最优的能力。在本文中，DE算法利用了所有粒子的pbest，目的是根据以下步骤生成新的改进位置。

首先，通过突变操作生成突变载体

 

其中r1和r2是在[1，2，…，N]范围内的随机数；F表示突变因子∈[0 , 1].

然后，如果随机生成的数r小于交叉常数CR，则用突变向量替换试验向量，否则，它取当前pbes的值。

最后，根据适应度函数的值（以最小化问题为例），由获胜者在生成的试验向量和相应的原始值之间更新pbest和gbest。

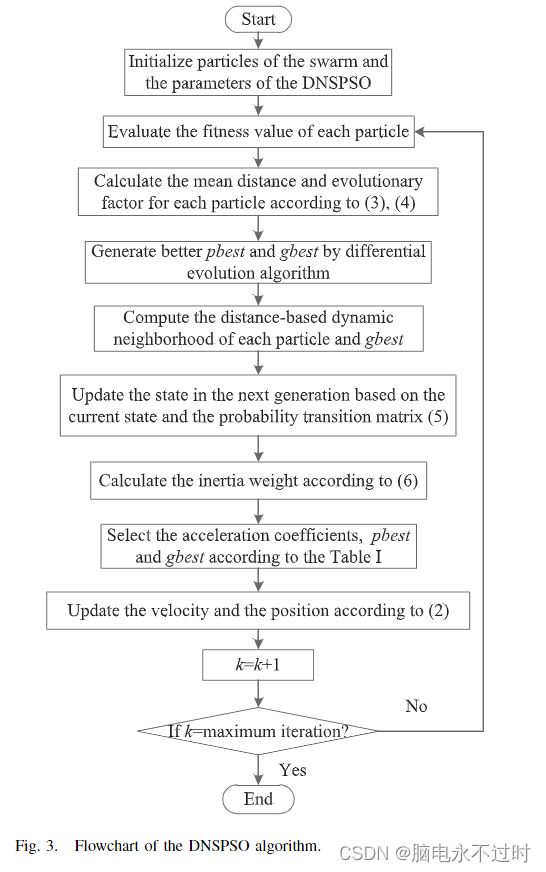
因此，DE算法完美地集成到了提出的DNSPSO方法中，建议的DNSPSO算法的流程图如图3所示。

四、 模拟实验

A、 实验设置

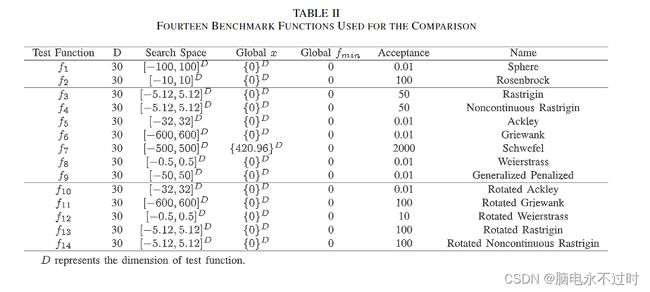
为了验证所提出的DNSPSO算法的有效性，根据单峰函数、多峰函数和旋转多峰函数对14个基准函数进行了实验[31]，[37]，[41]。需要指出的是，所开发的DNSPSO算法旨在提高粒子群算法在复杂多模态优化问题上的性能。f1（x）和f2（x）是被选为第一组基准函数的单峰函数。第二组由七个复多模态函数（f3（x）− f9（x）），其中包含大量局部最优。第三组包括四个旋转的多模态函数，其中旋转变量y是通过左乘正交矩阵M生成，描述为y=M∗x、 注意，正交矩阵是通过使用所罗门方法[31]生成的。所有基准函数的详细信息如表II所示，其中“acceptance”表示确定PSO算法找到的解决方案是否可接受的阈值。如果获得的解落入阈值内，则视为成功结果。

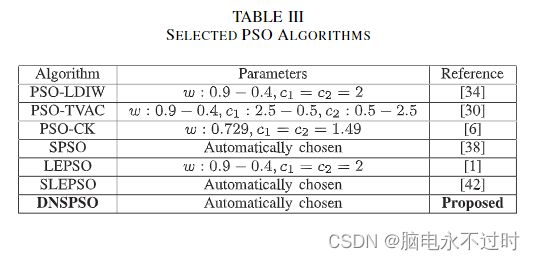
将DNSPSO算法的性能与六种现有PSO算法的性能进行了比较，包括PSOLDIW算法[34]、PSO-TVAC算法[30]、PSO-CK算法[6]、SPO算法[38]、LEPSO算法[1]和SLEPSO算法。

在所提出的DNSPSO算法中，转移概率π被设置为0.9，初始状态被设置为1（收敛状态）。两个邻域（pbest和gbest）的大小为5。在DE算法中，变异因子F从0.5线性增加到1，CR从0.9线性减少到0.4。请注意，其他六个PSO算法的参数是根据表III所示的相应参考设置的。

在我们的模拟中，群包含30个粒子，所有基准函数的维数为30。适应度评估（FEs）的数量设置为5×104。每个实验针对每个基准函数独立重复30次。

B、 求解精度的比较

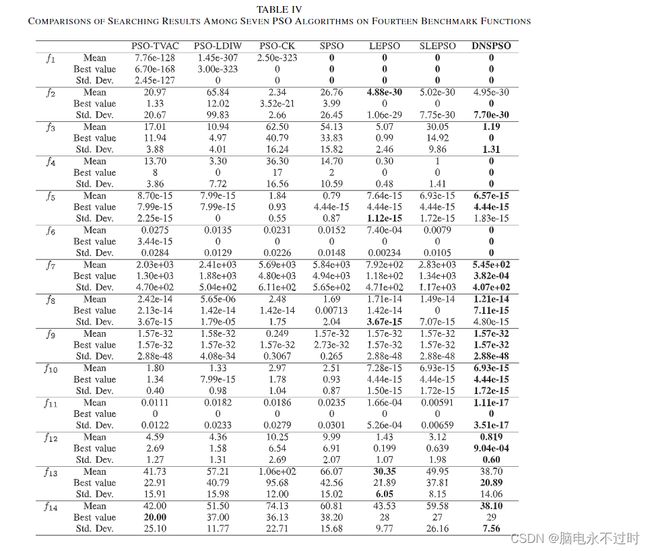
为了全面评估PSO算法的解质量，表IV中总结了每个基准函数的平均值、最佳值和标准差（Std.Dev.）值，其中最佳结果以粗体突出显示。为简单起见，图4以图形方式显示了应用于6个典型基准函数的7个PSO算法的平均适应值的收敛过程。

我们可以看到，在七个PSO算法中，DNSPSO算法在14个测试函数中的大多数上都取得了最佳性能。特别是，根据平均值，DNSPSO算法在12个函数（f1、f3-f12和f14）上排名第一，在f2和f13上排名第二。

具体地说，在表IV中，我们可以看到，SPSO算法、LEPSO算法、SLEPSO算法和DNSPSO方法在f1上获得了全局最小值。此外，DNSPSO算法在f2上获得了第二个最佳全局平均值，该值非常接近于最佳结果，具有最小的标准偏差值。因此，DNSPSO算法证明了在单峰问题上的竞争性能。

对于没有旋转的多模态问题，可以清楚地看到，所开发的DNSPSO算法比其他六种PSO算法表现得更好。从表IV和图4可以看出，当应用于f 3、f 4、f 6和f 7的函数时，DNSPSO算法大大提高了求解精度。请注意，DNSPSO算法在f 4和f 6上获得了全局结果f min。此外，就平均值和最佳值而言，所提出的DNSPSO算法在f 5和f 8上获得了最佳性能。对于f9，DNSPSO算法、PSO-TVAC算法、LEPSO算法以及SLEPSO算法都找到了令人满意的解决方案。值得一提的是，几个PSO算法在f9函数上获得了相同的平均值和最佳值，这反映了惩罚问题很容易陷入局部最优的事实

对于具有旋转的多模态问题，所开发的DNSPSO算法优于其他六种PSO算法。特别是，DNSPSO算法在求解f 11、f 12和f 14的函数时具有显著的性能−f 11上的17，f 12上的8，f 14上的38。对于f 10，LEPSO、SLEPSO和DNSPSO算法找到了一个接近的解，其中SLEPSO和DNSPO算法的结果略优于LEPSO算法获得的结果。同时，所提出的DNSPSO算法在f 13上排名第二，这与LEPSO算法获得的第一非常接近。需要指出的是，带旋转的优化问题的结果通常比不带旋转的最优化问题的结果差，这与问题复杂性的增加有关。

C、 收敛性能比较

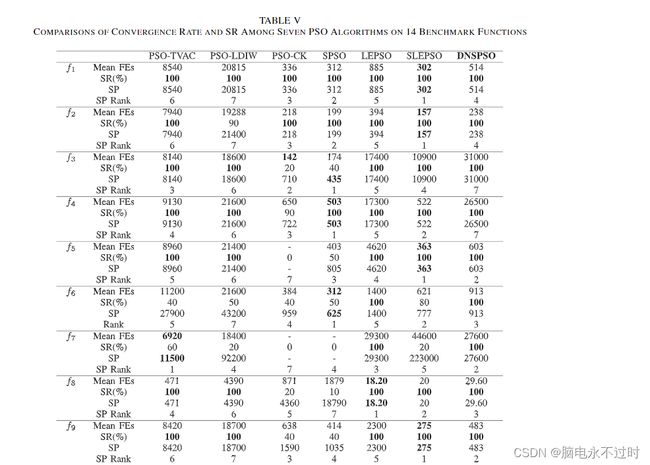
众所周知，收敛性能对进化算法至关重要。选择平均FEs、成功率[SR（%）]和成功绩效（SP）作为绩效指标[47]，以进行定量比较，如表V所示。平均FEs代表达到可接受解决方案所需的平均评估次数，值得注意的是，它只考虑了所有30次运行的“成功”轨迹。SR（%）表示每个测试功能的30次试验的成功百分比。由于某些PSO算法无法在某些函数的每条轨迹中搜索最优解，平均FEs无法全面证明PSO算法的收敛性能。因此，利用SP进一步评估进化性能，其中SP=（平均FEs/SR）。此外，表V中还列出了所选PSO算法的SP和SR的等级。应该提到的是，如果函数没有成功跟踪，则相应的SP等级为7

从表V中可以清楚地看出，DNSPSO算法在所有测试函数的可接受阈值内找到了一个解决方案，通过SR指数对所有基准函数进行100%验证。请注意，一些PSO算法在某些优化问题上的所有路径都失败，例如，PSO-CK在f 5、f 7和f 10上失败，SPSO在f 7和f 10上失败以及PSO-TVAC在f 10上故障。所提出的DNSPSO算法产生的可靠性最高，平均SR为100%，其次是LEPSO（98.57%）、SLEPSO（92.14%）、PSO-TWAC（85.71%）、PSO-LDIW（84.29%）、SPSO（60%）和PSO-CK（55%）。因此，DNSPSO算法是一种可靠的优化算法，在单峰和多峰问题上都有很高的成功率。

此外，当DNSPSO算法应用于优化大多数无旋转的多模态函数时，需要更小的平均FEs。特别是，DNSPSO算法通过获得三个第一和两个第二对五个带旋转的多模态函数，在滑坡中显著优于其他竞争者。同时，DNSPSO算法在f3和f4上获得最大的平均FEs，这可能是由包含大量局部极值的拉斯特里金和非连续拉斯特里金函数的特性引起的。请注意，DNSPSO算法获得的f3和f4的解精度大大超过了其他PSO算法，在4×104到5×104 FEs的范围内迅速下降，如图4所示。总之，开发的DNSPSO算法在单峰和多峰问题上都显示出令人满意的收敛速度，并且在多模态问题上显著优于其他PSO变体。

D、 邻域大小k的分析

邻域大小k的选择对于DNSPSO算法的性能至关重要。进行了一系列模拟实验，以了解邻域大小如何影响算法性能。在这项工作中，选择了两个单峰函数、三个不带旋转的多峰函数和两个带旋转的多峰函数来分析邻域大小。平均值、标准偏差、平均FEs和SR（%）的结果如表VI所示。应指出的是：1）DNSPSO算法对所有选定的具有不同k的七个函数获得100%的SR，2）SP的结果与平均FEs相同，因此未在表VI中显示。

对于球体优化问题，DNSPSO算法在不同的邻域大小下表现良好，而具有较小k的DNSPSO算法需要较小的平均FEs。对于复杂的单峰问题和Rosenbrock问题，不同k的DNSPSO算法的性能是不一致的。当k＝4和k＝5时，DNSPSO算法的结果比其他邻居大小的结果要好得多。对于没有旋转的多模态函数，k=4和k=5的DNSPSO算法在Rastrigin和Schwefel函数上表现出竞争性，并且当k为5和6时，它可以在Griewank上提供出色的性能。此外，具有不同邻域大小的DNSPSO算法在旋转的Ackley函数上获得相同的结果。特别地，当邻域大小k设置为6时，DNSPSO算法在旋转Griewank问题上实现全局最优。

因此，基于以上讨论，我们可以总结出邻域大小k对DNSPSO算法性能的影响，即：1）邻域大小kon对DNSPSO算法性能影响取决于优化问题的特性。对于单峰优化问题，邻域大小可以选择为较小的值。较大的邻域大小适用于多模态问题，尤其是旋转多模态问题；2）邻域大小与群大小有关。在本文中，邻域大小被设置为群大小的1/6。

五、 结论

本文提出了DNSPSO算法，以提高传统PSO算法的搜索能力。已经开发了基于距离的动态邻域，其中粒子的邻域在每次迭代时动态更新。根据搜索状态，通过切换学习策略自动调整DNSPSO算法的加速系数、个人最佳粒子和全局最佳粒子。DNSPSO算法中的粒子通过开发的基于距离的动态邻域共享信息，其中个人最佳粒子和全局最佳粒子被其相应邻域中随机选择的粒子替换。此外，DE算法已被用于进一步扩展粒子的搜索空间。实验结果表明，DNSPSO算法在14个广泛使用的基准函数上的解质量和收敛性能优于6个PSO变体，尤其是在复杂的多模态优化问题上。邻域大小对DNSPSO算法性能的影响也进行了全面的研究，并表明邻域大小的选择应基于优化问题的性质和群大小来确定。未来，我们的目标是进一步提高所开发的DNSPSO算法的收敛速度。我们还将DNSPSO算法应用于其他研究领域，如事件触发状态估计[9]、移动地平线估计[50]-[52]和自组织RBF神经网络