数据学习(5)·K-means 聚类和PCA算法

作者的课堂笔记[email protected]

Preview

• K-means 聚类
• 主成分分析（Principal Component Analysis）

---

无监督学习

和有监督学习类似，但是数据没有标签。给定输入数据，发现简化的特征，同时和输入的特征拥有同样的信息量。
一般来说，好的表示一般是低维度的，或者是稀疏表示的，也就是说大部分是0，又或者是独立的表示。

---

1 K-means 聚类问题

输入数据$\{x^{(1)}.....x^{(m)}\},x^{(i)}\in R^d$,K-means聚类将输入数据分成k类,$k\le n$来最小化每个类别内的平方和(WCSS).
$$argmi{n}_C\sum _{j=1}^k\sum _{x\in C_j}||x-{\mu }_j|{|}^2$$
等价问题：

• 最小化每个类内的方差${\sum }_{j=1}^k|C_j|Var(C_j)$.
• 最小化点之间的成对平方偏差在同一集群中：${\sum }_{i=1}^k\frac{1}{2|C_i|}{\sum }_{x,x‘\in C_i}||x-x‘|{|}^2$
• 最大化类与类之间的距离（BCSS）.

---

1.1 K-means聚类算法

• 优化K-means聚类是一个NP-hard问题，在欧式空间中。
• 通常通过启发式，迭代算法。
  Lloyd’s 算法
  

---

1.2 K-means聚类讨论

• K-means学习k维的稀疏表示，比如x使用one-hot编码，$z\in R^k$.
  $$z_j^{(i)}=1if{c}^{(i)}=j，otherwise0$$
  算法收敛于局部最优解，所以初始值的选择很重要！
• 怎样初始化$\mu$？均匀随机抽样（K-means++）,或者基于距离的采样。
• 怎么选择K？交叉验证或者G-means。

---

2 PCA(Principal Component Analysis)

消除特征之间的相关性，同时减少噪音。
给出$\{x^{(1)},...,x^{(m)}\},x^{(i)}\in R^n$.

• 发现一个线性的正交变换W：$R^n-R^k$针对输入数据。
• W 是将最大方差的方向和新坐标轴的方向对齐。
  正则化x,以便让$mean(x)=0,Stdev(x_j)=1$
• $x^{(i)}:=x^{(i)}-Mean(x)$
• $x_j^{(i)}:=x_j^{(i)}/Stdev(x_j)$
  

---

2.1 PCA表示学习

PCA 目标：

• 发现主要的组成$u_1,.....,u_n$他们相互正交，也就是不相关。
• $x$的大部分变化将由$k<<n$的$k$个主成分来解释。

PCA 的主要操作：

• 发现$x$的投影，$u_1^{T}x$覆盖最大的方差。
• 对$j=1,2,....,n$同样上述操作，找出互相正交的$u_1,.....,u_j$个方向。

---

2.2 寻找主成分

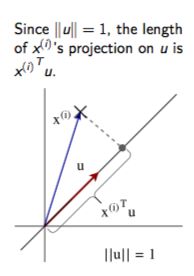
投影的方差：
$\frac{1}{m}{\sum }_{i=1}^m(x^{(i{)}^T}u{)}^2=\frac{1}{m}{\sum }_{i=1}^m{u}^T{x}^{(i)}{x}^{(i{)}^T}u=u^T(\frac{1}{m}{\sum }_{i=1}^m{x}^{(i)}{x}^{(i{)}^T})u=u^T\Sigma u$
$\Sigma :$是样本的协方差矩阵。

---

2.3 第一主要成分

发现一个$u_1$最大化投影方差：
$$u_1=argma{x}_{u:||u||=1}{u}^T\Sigma u$$
$u_1$被称为$x$的第一主成分。同时$u_1$是协方差矩阵的最大特征向量。

---

证明：$u_1$是协方差矩阵的最大特征向量。
使用拉格朗日函数：
$$L(u)=-u^T\Sigma u+\beta (u^{T}u-1)$$
最小化$L(u)$.
$$\frac{\partial L}{\partial u}=-2\Sigma u+2\beta u=0$$
所以$\Sigma u=\beta u$,因此$u_1$是$\Sigma$的特征向量。$u=v_j$,是第$j$大的特征值对应的特征向量。
$$u^T\Sigma u=v_j^T\Sigma v_j={\lambda }_j{v}_j^T{v}_j={\lambda }_j$$
因此$u_1=v_1$特征向量对应最大的特征值。

---

证明：第j个主成分，$u_j$是第j大的协方差矩阵的特征向量。
j=2
$$u_2=argma{x}_{||u||=1,u_1^{T}u=0}{u}^T\Sigma u$$
拉格朗日函数：
$$L(u)=-u^T\Sigma u+{\beta }_1(u^{T}u-1)+{\beta }_2(u_1^{T}u)$$
最小化$L(u):$
$${\beta }_2=0,\Sigma u={\beta }_{1}u$$
最大化$u^T\Sigma u=\lambda ,u_2$必须是第二大特征值对应的特征向量${\beta }_1={\lambda }_2$.

---

2.4 PCA性质

• 主成分投影的方差是：$Var(x^T{u}_j)=u_j^T\Sigma u_j={\lambda }_j$,j=1,2…n
• % 由第j主成分解释的方差可以被表示成$\frac{{\lambda }_j}{{\sum }_{i=1}^n{\lambda }_i}$
• 同样可通过前K主成分解释$\frac{{\sum }_{j=1}^k{\lambda }_j}{{\sum }_{j=1}^n{\lambda }_j}$

---

2.5 PCA 投影

样本在主成分空间的投影：
$$z^{(i)}=\left[\begin{array}{c}{x}^{(i{)}^T}{u}_1\\ ....\\ x^{(i{)}^T}{u}_n\end{array}\right]\in R^n$$
矩阵表示：
$$z^{(i)}={\left[\begin{array}{ccc}....& ....& ....\\ u_1& ....& u_n\\ ....& ....& ....\end{array}\right]}^T{x}^{(i)}=W^T{x}^{(i)},orZ=XW$$
仅用前K个主成分用来降维。

---

2.5 PCA理解

PCA移除了输入数据的冗余。
$Z=XW$为PCA的投影数据。
$$cov(Z)=\frac{1}{n}{Z}^{T}Z=\frac{1}{n}(XW{)}^T(XW)=W^T(\frac{1}{n}{X}^{T}X)W=W^T\Sigma W$$
因为$\Sigma$是对称的，有特征值，特征分解为：
$$\Sigma =W\Lambda W^T$$
$$W=\left[\begin{array}{ccc}....& ....& ....\\ u_1& ....& u_n\\ ....& ....& ....\end{array}\right],\Lambda =\left[\begin{array}{ccc}{\lambda }_1& ....& ....\\ ....& ....& ....\\ ....& ....& {\lambda }_n\end{array}\right]$$
$$cov(Z)=W^T(W\Lambda W^T)W=\Lambda$$
主成分变换$XW$对角化$X$的样本协方差矩阵。

---

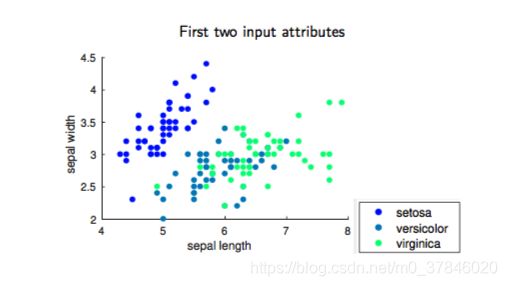
2.6 PCA例子

鸢尾花数据

---

人脸特征

---

2.7 PCA 的缺点

• 只考虑了数据特征之间的线性关系
• 假设数据是真实并且连续的
• 假设输入空间的近似正态性（但在实践中，对于非正态分布的数据仍然可以很好）

非正态分布输入：

---

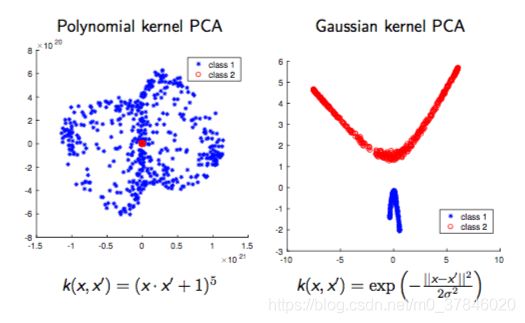
2.7 PCA核心

利用PCA特征提取。

线性的PCA假设数据在$R^n$是可分的.
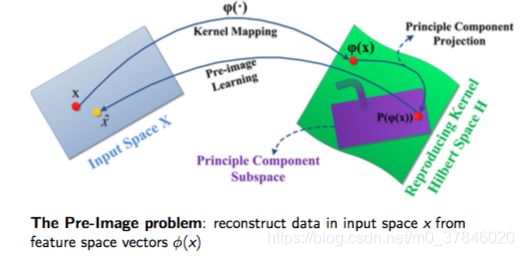
非线性推广：

• 将数据投影到更高维度使用特征映射。$R^n\to R^d(d\ge n)$
• 特征映射通过定义核函数$K(x^{(i)},x^{(j)})=\varphi (x^{(i)}{)}^T\varphi (x^{(j)})$或者核矩阵$K\in R^{m\times n}$

---

特征映射数据的样本的协方差矩阵：
$$\Sigma =\frac{1}{m}\sum _{i=1}^m\varphi (x^{(i)})\varphi (x^{(i)}{)}^T\in R^{d\times d}$$
让$({\lambda }_k,v_k),k=1,....d$是$\Sigma$的特征分解。
$$\Sigma v_k={\lambda }_k{v}_k$$
$x^{(l)}$在第k主成分$v_k$的PCA投影是：
$$\varphi (x^{(l)}{)}^T{v}_k$$
为了避免计算$\varphi (x^{(l)})$,于是：
$$\Sigma v_k=(\frac{1}{m}\sum _{i=1}^m\varphi (x^{(i)})\varphi (x^{(i)}{)}^T)v_k={\lambda }_k{v}_k$$
把$v_k$写成$\varphi (x^{(1)})....\varphi (x^{(m)})$的线性组合：
$$v_k=\sum _{i=1}^m{\alpha }_k^i\varphi (x^{(i)})$$
$x^{(l)}$的PCA投影通过使用K函数表示：
$$\varphi (x^{(l)}{)}^T{v}_k=\varphi (x^{(l)}{)}^T\sum _{i=1}^m{\alpha }_k^i\varphi (x^{(i)})=\sum _{i=1}^m{\alpha }_k^{i}K(x^{(l)},x^{(i)})$$
怎么计算${\alpha }_k^i$:
$$\Sigma v_k=(\frac{1}{m}\sum _{i=1}^m\varphi (x^{(i)})\varphi (x^{(i)}{)}^T)v_k={\lambda }_k{v}_k$$
用$v_k={\sum }_{i=1}^m{\alpha }_k^i\varphi (x^{(i)})$代替：
$$K{\alpha }_k={\lambda }_{k}m{\alpha }_k$$
于是${\alpha }_k=\left[\begin{array}{c}{\alpha }_k^1\\ ....\\ {\alpha }_k^m\end{array}\right]$可以通过求K的特征分解来得出。
正则化${\alpha }_k$以便于使$v_k^T{v}_k=1$
$$v_k^T{v}_k=\sum _{i=1}^m\sum _{j=1}^m{\alpha }_k^i{\alpha }_k^j\varphi (x^{(i)}{)}^T\varphi (x^{(j)})={\alpha }_k^{T}K{\alpha }_k={\lambda }_{k}m({\alpha }_k^T{\alpha }_k)$$
$$||{\alpha }_k|{|}^2=\frac{1}{{\lambda }_{k}m}$$
当$E(\varphi (x))̸=0$,我们需要重新计算$\varphi (x)$:
$$\hat{\varphi }(x^{(i)})=\varphi (x^{(i)})-\frac{1}{m}\sum _{l=1}^m\hat{\varphi }(x^{(l)})$$
中心化之后的K函数：
$${\hat{K}}_{i,j}=\hat{\varphi }(x^{(i)}{)}^T\hat{\varphi }(x^{(j)})$$
矩阵表示：
$$\hat{K}=K-1_{m}K-K{1}_m+1_{m}K{1}_m,1_m=\left[\begin{array}{ccc}\frac{1}{m}& ....& \frac{1}{m}\\ ....& ....& ....\\ \frac{1}{m}& ....& \frac{1}{m}\end{array}\right]$$
然后使用$\hat{K}$来计算PCA.

---

• 经常在聚类、异常检测中使用PCA.
• 投影到k维约简子空间一般是不可能的.
  

---

2.8 总结

表示学习：

• 把一些特征表达的更加简单和便于理解。
• 通常在特征提取、降维、分类问题中使用。