循环世界模型(Recurrent World Models)——真实世界建模的强化学习利器
世界模型
智能体可以在它们头脑中的世界进行学习吗?
世界模型(World Model)是NIPS 2018获得口头报告的论文之一,也是谷歌AI和Deepmind 2019年力作深度规划网络 PlaNet的主要参考文献之一。这篇博文是对World Model论文的翻译和学习笔记。原文地址 https://arxiv.org/abs/1803.10122
摘要
我们探索建立通用强化学习环境的生成神经网络模型。我们的世界模型能够以一种快速的无监督学习方式,学习一个压缩的空间和时间的环境表示(Environment Representation)。通过使用从世界模型中提取的特征作为智能体的输入,我们可以训练出一个非常紧凑、简单的策略来解决所需的任务。我们甚至可以将智能体完全训练在由它的世界模型所产生的幻想的环境(own dream environment)中,并将这一策略转移到真实世界的环境中。
1. Introduction

人类以有限的感官所能感知到的事物为基础,形成了一个心理世界模型(mental model of the world)。我们所做的决定和行动都是基于这个内部模型。系统动力学之父杰伊·赖特(Jay Wright)将心理模型描述为:
“我们脑中所承载的周围世界的形象,只是一个模型。他脑子里没有办法能把世界、政府或国家都搞清楚。他只选择了(他理解的世界政府国家的)概念和它们之间的关系,并使用这些概念来表示真实的系统。”
为了处理流经我们日常生活的大量信息,我们的大脑学会了信息的空间域和时域的抽象表示。我们能够观察一个场景并记住其中的抽象描述[4,5]。证据还表明,我们在任何时刻所感知的,都是由我们的大脑根据我们的内部心理模型对未来的预测所决定的。(比如下图,我们的大脑认为左图的两个正方形并不标准,认为右图的黑白点在不停波动,这些都是大脑根据我们的视觉系统建立了自己的模型,而后做出的判断,但真实世界并非如此。)
有一种理解大脑内部预测模型的方法是,internal model可能不仅仅是预测未来,而且根据我们当前的运动行为来预测未来的感官数据。我们能够在这种预测模型上采取行动,并在我们面临危险时表现出快速的行为[13],而不需要有意识地规划一个行动路线。以棒球为例,一个棒球运动员只有毫秒级的时间来决定如何挥动球棍,这个时间甚至比视觉信号从眼球传到大脑的时间还要短。对专业运动员来说,这个动作几乎是下意识的,他们的肌肉在正确的时间和地点挥动球棍,与他们内部模型的预测一致[7]。他们可以根据他们对未来的预测迅速采取行动,而不需要有意识地推出可行的击球计划。
在许多强化学习问题中,智能体既需要一个对过去和现在状态的良好描述,还需要一个优秀的模型来预测未来的状态,最好是一个如递归神经网络RNN一样的强大的预测模型。
大参数量的RNN模型是具有高度表示能力的模型(强大的表征能力可能代表强大的决策能力),可以学习丰富的数据空间和时间表示(Spatial and temporal representation)。然而,许多文献中的model-free的强化学习算法往往只采用参数较少的小型神经网络。传统RL算法受限于credit assignment问题。
PS:credit assignment问题是说,在许多RL任务中,reward都是很稀疏的,往往在一串序列结束后才给出,而在这之前agent已经采取了很多action,credit assignment 问题就是要解决究竟是哪一个action对最后的reward的影响最大,对final reward,哪些action起了有益的作用,哪些action起了负面作用。credit assignment问题使得传统的RL算法很难训练数百万个参数的大模型,因此在实际应用中,由于小网络在训练过程中更快,反而有比较好的策略。(我的直观理解就是,由于sparse reward,大型网络的参数很不好训练,所以在性能上输给了小型网络,但作者认为采用小型网络只是暂时的成功,未来要用的还是大型网络)
理想情况下,我们希望能够训练大参数量的RNN模型,比如我们已经有了训练大规模网络的反向传播算法。因此这篇论文的工作就是探讨如何训练一个大型网络来解决强化学习的任务。在文中我们讨论的大型网络是指参数量在 1 0 7 10^7 107量级的网络,相比 1 0 3 − 1 0 6 10^3-10^6 103−106量级的小型网络,这是一个进步,但是和深度学习领域最成功的巨型网络相比还是太小,后者具有高达 1 0 8 − 1 0 9 10^8-10^9 108−109量级的参数规模。
我们把agent模型拆分成两部分,一部分是大型的world model,另一部分是小型的controller model。首先采用无监督学习的方式训练world model,作为对真实世界的一个表征,或者叫agent本身对真实世界的一个理解,也就是前文所述的mental model。然后再训练controller model利用学到的world model去完成切实的RL任务。controller model使训练算法在一个较小的搜索空间上处理credit assignment问题,而不是牺牲capacity和表达能力,在更大的世界模型上处理credit assignment问题。通过使controller model从world model的视角下进行训练,我们发现它可以学习到一种高度紧凑的策略来执行它的任务。
虽然目前有大量的研究有关model-based强化学习算法,但本文并不是要做一个这方面的综述。相反,本文的目标是从1990-2015年一系列论文中凝练出几个关键的概念,这些概念是融合了RNN-based world model和controller model 领域的。我们还将讨论其他相关的工作,(相关工作指,学习一个世界模型和然后使用该模型训练controller等类似思想的论文)。
在本文中,我们还提出了一个简化框架,用于在实验中展示论文提到的若干核心观点。同时提出了一些前瞻性见解,以便将这些idea应用于不同的RL算法框架。本文的RL领域的学术术语和标记与On Learning to Think:Algorithmic Information Theory for Novel Combinations of RL Controllers and RNN World Models该文章保持一致。

我们搭建了一个基于OpenAI Gym的概率生成模型。我们采用从真实实验环境中收集到的观察数据训练RNN-based world model。当world model训练好之后,可以用来模拟真实环境,或者训练controller。
2. 智能体模型 Agent Model
受我们人类的认知系统启发,本文提出了一个简单的智能体模型。模型包括一个视觉感知组件(Visual Sensory Component),它将看到的图像压缩成一个低维的表征向量(Representative code)作为模型的输入。模型还包括一个记忆组件(memory component),记忆组件基于历史信息,对未来的表征向量做出预测。最后,我们的模型还有一个决策组件(decision-making component),它仅仅基于视觉组件和记忆组件的表征向量决定采取的动作。

如上图,视觉组件和记忆组件组成了World Model,决策组件就是前文所述的controller model。每个时间步骤下,视觉组件将高维的原始图像编码成一个低维的潜层向量,记忆组件接收视觉组件编码的潜层向量,并基于其本身的历史信息,对未来状态做出预测。决策/控制组件同时接受视觉组件(V)和记忆组件(M)的输出,采取动作,与真实环境进行交互。
2.1 变分自编码器(VAE)模型——即视觉(V)组件
在每个时间步长,真实环境给智能体的输入是一个高维图像观测信息(文中叫high dimensional input observation,所谓高维信息是指图像作为一个三维矩阵,尺寸比较大)。视觉组件的输入是一个二维的图像帧,通常是视频序列的一部分。视觉组件的任务就是学习一个抽象的、压缩的表示(Representation)来描述每一帧的输入。

论文中使用了一个简单的变分自编码器作为视觉组件,VAE能够将原始观察图像通过编码成一个低维潜层向量 z z z,再经过解码器,解码成重构图像。向量 z z z就是我们需要的低维潜层向量(small latent vector)。
2.2 MDN-RNN模型——记忆组件
视觉组件的任务是将输入图像进行压缩,我们同时也希望将时域上的信息也进行压缩。为实现这个目的,记忆组件的任务就是预测未来。详细地说,记忆组件需要预测出视觉组件在未来可能输出的潜层向量 z z z,换句话说,记忆组件需要预见将要发生的游戏画面(的潜层表征)。由于自然环境中许多复杂的模型都是随机性的,因此我们训练RNN模型去输出 z z z的概率密度函数 p ( z ) p(z) p(z),而不是输出一个确定的向量 z z z。
在论文在中,我们用混合高斯分布(a mixture of Gaussian Distribution)来估计 p ( z ) p(z) p(z)。给定当前信息和历史信息,我们训练RNN来输出下一个潜层向量 z t + 1 z_{t+1} zt+1的概率分布(如何输出概率密度?)。
确切地说,RNN建模的是这样一个条件概率: P ( z t + 1 ∣ a t , z t , h t ) P(z_{t+1}|a_t,z_t,h_t) P(zt+1∣at,zt,ht),式中, a t a_t at是 t t t时刻智能体采取的动作, h t h_t ht是RNN模型在 t t t时刻的隐层状态。在采样过程中,我们通过控制温度参数 τ \tau τ来控制模型的不确定性(具体是怎样控制的?),而且实验发现 τ \tau τ值对接下来的controller model的训练是有帮助的。

生成概率密度的方法被称作是MDN-RNN模型,MDN是混合密度网络(Mixture Density Network)的简称,由大名鼎鼎的《模式识别与机器学习》的作者CM.Bishop发明。MDN-RNN模型先前被应用于序列生成问题,比如手写字或简笔画的生成。下图是SketchRNN的例子,图中竖线左边是人画的第一笔,模型可以根据这一笔线条预测之后画的内容。在本文中,我们并不用它来预测简笔画,而是预测下一步视觉组件要输出的潜层向量 z t z_t zt。

2.3 Controller ( C ) Model
controller model负责确定要采取的action,以使一轮rollout的期望回报最大。在本文的实验中,我们故意使controller model的参数规模尽可能的小,并且和视觉组件、记忆组件分开训练,这样就能保证智能体的多样性大部分都集中在世界模型中(也就是V和M模型)。
Controller Model是一个简单的单层线性模型,将 z t z_t zt和 h t h_t ht直接映射到动作空间 a t a_t at:
a t = W c [ z t h t ] + b c a_t = W_c\ [z_t\ h_t]+b_c at=Wc [zt ht]+bc
在上式中, W c W_c Wc是权重矩阵, b c b_c bc是偏置向量,controller model首先将 z t z_t zt和 h t h_t ht向量拼接在一起,然后进行线性映射,得到动作 a t a_t at。
2.4 将V,C,M模型进行整合
下图展示了V,M,C模型是如何整合在一起,并与环境进行交互的。在每个时刻 t t t,首先由V模型处理原始图像,得到 z t z_t zt,随后,C模型将 z t z_t zt向量与M模块的 h t h_t ht向量进行拼接,并输出动作向量 a t a_t at,完成与环境的交互。最后将 z t z_t zt和 a t a_t at输入M模型,更新隐状态 h t + 1 h_{t+1} ht+1。

下面给出在OpenAI Gym环境下的整体模型的伪代码。给定一个controller model,在这个函数下运行,就能得到一个episode的累计回报值。
def rollout(controller):
'''
env,rnn,vae are global variables
'''
obs = env.reset() # 初始化游戏环境
h = rnn.initial_state() # 获取初始的RNN隐状态
done = False # 游戏结束标志
cumulative_reward = 0 # 累计回报
while not done:
z = vae.encode(obs) # VAE模型对原始图像进行编码
a = controller.action([z, h]) # controller model根据当前状态z和之前隐状态h采取动作
obs, reward, done = env.step(a) # agent与环境交互,得到下一个时刻的环境状态和reward
cumulative_reward += reward # 更新累计回报
h = rnn.forward([a, z, h]) # 更新隐状态
return cumulative_reward
controller model的minimal design(我的理解是,minimal design是将controller model的参数量设计得比较小的这一做法)也具有非常重要的实践意义。深度学习领域的研究进展给我们提供了高效训练大规模复杂神经网络的工具,也提供了设计一个可微的、性能良好的损失函数的可能。我们的V模型和M模型就是在多GPU加速的反向传播算法上训练得到的,因此我们希望模型的大部分复杂性以及模型的参数都驻留在V模型和M模型中(不理解原文中这句话前后的逻辑在哪里,设计一个小controller和较大的V,M模型是有助于将(从真实环境学来的)模型复杂性留存在VM模型中,但这和反向传播算法有什么关系?)。相比来说,controller model这一线性模型的参数量是最小的了,这就给我们用非传统算法来训练controller model提供了可能。比如,我们甚至可以用进化算法来处理复杂RL问题的credit assignment问题。
我们用Covariance Matrix Adaptation Evolution Strategy(CMA-ES)算法来实际优化controller model的参数。CMA-ES算法因解决上千维参数空间的优化问题的能力而著名。在进化Controller model的参数时,用单机多核就可以并行运行多个rollout展开训练。具体的模型结构、训练细节、环境配置请见下面的附录部分。
3. 赛车(Car Racing)实验
在本节,我们阐述如何利用上文所述的模型解决一个赛车竞速的RL任务。据据目前所知,本文的智能体是首个解决赛车任务的智能体。我们之所以对这个游戏感兴趣,是因为这个游戏不是很难训练——让赛车在随机生成的轨道上摇摇晃晃地跑起来,而且得到分数还算中等。CarRacing-v0游戏定义了解决这个游戏的标准——在100次连续尝试中取得平均900分的成绩,这要求智能体必须极少犯错误。

3.1 特征提取环节的世界模型
一个预测性世界模型(predictive world model)可以有效地提取空域与时域特征。将这些特征应用于controller model,就可以训练一个紧凑的、最小的controller model来完成连续域控制任务,就比如说以像素级图像作为输入的CarRacing-v0俯视角的赛车游戏。
在实验中,每次游戏的赛道都是随机生成的,当agent控制赛车驶过一个小砖块时,得到奖励,因此目标是尽可能多地驶过砖块,在最少的时间内获得尽可能多的分数。agent能够控制的是左转、右转、加速、刹车四个动作。
为训练视觉组件(V模型),首先收集10000个episode的游戏数据集。我们用一个随机策略的agent在赛道上乱跑,记录下 a t a_t at 和由此导致的环境状态 o t o_t ot 。我们用这个数据集训练VAE模型,将每一帧图像编码成潜层向量,训练过程是以自编码器的重构误差为驱动的。
现在有了能够感知原始视觉环境的V模型之后,我们用V模型把上一步的数据集中的 o t o_t ot经过V模型处理,也存到数据集中。随后利用预处理的数据训练MDN-RNN模型,用以建模 P ( z t + 1 ∣ a t , z t , h t ) P(z_{t+1}|a_t,z_t,h_t) P(zt+1∣at,zt,ht),看做是一个混合高斯分布(如何理解a mixture of Gaussians这个概念?)。(PS: 在原则上,我们可以端到端地训练整个模型,但我们发现分开训练更具有实际意义,而且也能得到满意的结果。分开训练的话,只需要单机单卡,不到1小时就能完成。我们在分别训练VAE和MDN-RNN时,不必费劲心力地调整模型的超参数。)
在实验中,世界模型(指V模型和M模型)没有接触到任何的,从真实环境反馈的reward信息,世界模型的任务就只是压缩观察到的原始图像,并作出下一帧图像的预测。只有Controller Model才能接触到真实环境反馈的reward(PS:但是controller接触不到真实的环境,它只能利用world model 对真实世界的建模来做决策,这个和唯物主义认识论、实践论的观点颇为相近,人的意识是物质世界的反映,但不一定完全真实,人的行为都是建立在自己脑子里的、对物质世界的观点和印象上的,人通过社会实践、生产实践来逐步完善自己对物质世界的认知,进而影响我们的行为。)在controller model中,只有867个参数,规模较小,所以CMA-ES这种进化优化算法才能比较适合。
VAE模型可以重构游戏中的画面,借此,我们可以将模型关注什么信息进行可视化,下图是用游戏截图进行重构的结果。可以看到重构结果丢失了车道上的一些信息,但是整个画面的重点信息都感知到了。

在这篇论文的在线版本上,demo可以随机导入图像,编码为一个15维的低维潜层向量,并生成对应的重构图。同时也可以调整 z z z的各个维度的值,观察 z z z向量如何影响重构结果。
3.2 实验过程
赛车任务遵循如下的步骤:
- 用随机策略收集10000盘游戏的记录;
- 训练VAE模型将原图像帧编码成32维向量 z ∈ R 32 z \in R^{32} z∈R32;
- 训练MDN-RNN模型,对 P ( z t + 1 ∣ a t , z t , h t ) P(z_{t+1}|a_t,z_t,h_t) P(zt+1∣at,zt,ht)进行建模;
- Controller model的形式如 a t = W c [ z t h t ] + b c a_t = W_c\ [z_t \ h_t]+b_c at=Wc [zt ht]+bc;
- 应用CMA-ES模型求解 W c W_c Wc和 b c b_c bc使得期望reward最大化。
| 模型 | 参数量 |
|---|---|
| VAE | 4,348,547 |
| MDN-RNN | 422,368 |
| Controller | 867 |
3.3 实验结果
3.3.1 只用 V Model
如果对原始图像有了一个很好的表征(Representation),那么让智能体学会开车不是个很难的事。之前的研究关注于利用手工设计的视觉特征对raw observation进行描述,比如LIDAR特征、角度信息、位置和速度信息等等。利用这些手工设计特征,搭建一个小型神经网络,可以很容易得到一个满意的驾车策略。因此,我们让controller model只依靠视觉模型而不依赖M模型能否完成任务。此时的controller model设计为 a t = W c ⋅ z t + b c a_t = W_c\cdot z_t+b_c at=Wc⋅zt+bc。

尽管赛车还能沿着赛道跑,但是在急弯处赛车就开始摇摇晃晃,离开了赛道。在100次实验中,仅使用V模型的智能体得分为 632 ± 251 632\pm 251 632±251,与OpenAI Gym的积分榜上的传统深度强化学习算法(比如A3C)水平相当。如果在controller model中加入一个hidden layer,智能体的表现可以提升到 788 ± 141 788\pm141 788±141,但是这仍不足以解决这个问题。
3.3.2 完整世界模型(V和M模型)
V模型只能是将当前画面编码成低维特征向量,能够感知当下信息,但是预测能力几乎没有。与之相反的是,M模型只做一件事,而且做的非常好,就是预测 z t + 1 z_{t+1} zt+1。因为M模型的预测 z t + 1 z_{t+1} zt+1是由RNN的隐状态 h t h_t ht产生的,所以它作为学习到的特征,送入controller的话会比较适合。所以,将 z t z_t zt和 h t h_t ht拼起来,作为对当前状态和未来状态的表征,就非常适合做为controller的输入向量。

可以看到上图中,有了M模型的加入,赛车在经过急弯时表现就稳定得多。同时利用 h t h_t ht和 z t z_t zt特征可以显著提升智能体的表现性能。此外,我们认为,在汽车比赛过程中,在做出这些快速反射性的驾驶决策时,智能体不需要提前计划并推出未来的假想场景。由于 h t h_t ht包含关于未来状态的概率分布信息,所以智能体可以本能地查询RNN以指导其动作决策。与先前讨论的一个老练的赛车驾驶员或棒球运动员一样,该智能体可以本能地预测在最激烈的赛道上如何飙车。
| 算法 | 平均得分 |
|---|---|
| DQN | 343 ± 18 343\pm 18 343±18 |
| A3C (Continuous) | 591 ± 45 591\pm 45 591±45 |
| A3C (Discrete) | 652 ± 10 652\pm 10 652±10 |
| CEOBILLIONAIRE (Gym平台积分榜) | 838 ± 11 838\pm 11 838±11 |
| V模型 | 632 ± 251 632\pm 251 632±251 |
| V模型+单隐层 | 788 ± 141 788\pm 141 788±141 |
| World Model(V & M模型) | 906 ± 21 \bm{906\pm 21} 906±21 |
如上图所示,agent可以达到 906 ± 21 906\pm21 906±21的高分,比较有效地解决了这个问题,而且是目前最高的分数。之前的深度强化学习算法得分都在 591 − 652 591-652 591−652之间,最好的记录是 838 ± 11 838\pm 11 838±11。传统算法一般需要对每帧图像做预处理,比如角点检测,或者输入模型的是连续若干帧图像的堆叠(应该是用于感知时域信息,和AlphaGo Zero的input方式很像)。相比而言,本文的world model只需要输入原始的RGB图像,就能从中直接学到时域-空域的representation。据目前所知,这是首次采用该类方法解决这种强化学习任务。
3.4 世界模型“眼中的”CarRacing游戏
因为世界模型能够对未来的游戏状态进行建模,因此我们使其生成它“想象中的”CarRacing游戏场景(或者说,一个假的,凭空生成的游戏状态)。给定模型当前状态,生成 z t + 1 z_{t+1} zt+1的概率分布,然后从中采样一个 z t + 1 z_{t+1} zt+1,将这个 z t + 1 z_{t+1} zt+1当做真实的游戏状态生成的。将这个虚拟状态送进controller model,可以得到智能体对这个“梦境”中的状态的反应,也可以将其送入VAE模型,通过解码得到可视化的“梦境”场景。在论文的在线版本上可以调整 τ \tau τ 的值,以控制M模型生成的“梦境”的不确定性。
4. VizDoom游戏实验
4.1 在“梦境”中学习RL任务
我们刚刚看到,在真实环境中学到的控制策略在梦境(或者说,世界模型)中发挥了一定的作用。这就是我们的问题——我们能否训练智能体在自己的梦境中学习,并将学到的策略迁移到真实环境中呢?
如果我们的世界模型(World Model)对于它的目的是足够准确的,并且对眼前问题的认识足够完整的话,我们应该能够用这个世界模型(World Model)来代替实际的环境。毕竟,我们的Agent并没有直接观察真实环境,而只是看到了世界模型(World Model)让它看到的东西。因此在这个实验中,我们在一个由世界模型(World Model)所产生虚幻环境下训练了一个Agent,这个agent的world model被训练用于尽可能地模仿VizDoom游戏的环境。

agent必须学会躲避房间另一侧的怪兽射过来的火球,以免被杀死。这个游戏没有明确的reward,所以为了尽可能地模仿人类的操作,RL任务的累计回报可以定义为一局游戏中agent存活的时间,活得越久,分数就越高。每个episode大约有2100个时间步长,约合60秒。解决这个游戏(或者说,agent达到人类的水准)需要至少在100盘游戏中,平均存活750个step,也就是约20秒的时间。
4.2 实验过程
VizDoom的实验过程和CarRacing大致相同。几个关键不同在于:CarRacing游戏中,M模型只需要预测下一个step的游戏状态,但是VizDoom游戏里,M模型还需要预测下一个step会不会死亡,也就是输出一个二值变量 d o n e t done_t donet,简称 d t d_t dt。
因为模型能够预测未来是否死亡,实际上这就具备了模型一个完整RL环境的所有信息。我们把M模型封装成OpenAI Gym的游戏环境,用来构建一个虚拟的游戏environment(尽管封装好的内核里面,游戏的运行机制和真实的游戏并不一样,但是M模型能够给出是否死亡、下一时刻的游戏状态等等信息,因此就足以模拟真实环境的所有功能了)。
在虚拟的环境中训练时,不需要V模型编码假的游戏状态,而是只用潜层空间环境来训练智能体。只会带来一系列好处,接下来会一一讲到。
因为用M模型模拟的虚拟游戏和真实游戏的接口是一样的,所以agent在虚拟环境中也能学的很好。这是我们就可以将游戏策略迁移到真实环境中,观察迁移效果如何。(也就是看看,仅凭Agent想象的世界中学习,能不能在真实世界中也奏效)。
我们也总结了一个实验步骤如下。
- 用随机策略收集10000盘游戏的记录(应该是从真实环境中收集数据,不然一开始M模型对游戏机制一无所知,又怎么能模拟真实游戏环境呢?下文的叙述应该是证实了我这个思路);
- 训练VAE模型将原图像帧编码成64维向量 z ∈ R 64 z \in R^{64} z∈R64;
- 训练MDN-RNN模型,对 P ( z t + 1 , d t + 1 ∣ a t , z t , h t ) P(z_{t+1},d_{t+1}|a_t,z_t,h_t) P(zt+1,dt+1∣at,zt,ht)进行建模;
- Controller model的形式如 a t = W c [ z t h t ] a_t = W_c\ [z_t \ h_t] at=Wc [zt ht];
- 应用CMA-ES模型求解 W c W_c Wc使得在虚拟游戏环境中的期望reward最大化。
- 应用上步骤学到的policy在真实游戏环境中测试。
模型的参数量也有了相应的调整。
| 模型 | 参数量 |
|---|---|
| VAE | 4,446,915 |
| MDN-RNN | 1,678,785 |
| Controller | 1088 |
4.3 在“梦境”中学习 Training Inside of the Dream
经过一段时间的训练,在由M模型产生的虚拟游戏环境中,agent已经学会如何躲子弹了。在虚拟环境中,agent的得分大约在900个step左右(解决这个问题要求agent的得分在750个step)。下图是M模型生成的虚拟游戏环境。

在这里,基于RNN的世界模型World Model被训练成模仿一个由人类程序员设计的完整的游戏环境。它仅从随机策略的episode中收集的原始图像数据中学习,学习如何模拟游戏的基本方面,例如游戏逻辑、敌人行为、物理以及三维图形绘制。
例如,如果agent选择了向左移动,M模型就会学到将agent移动到左侧,并相应地调整其游戏状态的潜层表示(人物移动了,游戏视角就要相应变化)。如果agent试图在任一方向上移动太远,它也会学到阻止agent移动到两侧的墙之外。有时,M模型需要跟踪从几个不同的怪物射出的多个火球,并沿着它们的预期方向一致地移动火球。它还必须检测agent是否被这些火球中的一个杀死。总而言之,从random policy的episode收集的数据训练一个对游戏运行机制一无所知的M模型,使它能够逐渐掌握游戏的规则、机制,这就相当于在一个人的头脑中构建了对这个游戏的完整的认识,这样,这个人玩游戏就会无往不利。
然而,与实际游戏环境不同,我们注意到,可以在虚拟环境中增加额外的不确定性,从而使得虚拟环境游戏更具挑战性。我们通过提高 z t + 1 z_{t+1} zt+1采样过程中的温度参数 τ \tau τ 值来增加上述这种不确定性。通过增加不确定性,与实际环境相比,我们的虚拟环境变得更加困难。与实际的游戏相比,火球可以在较低可预测的路径中更随机地移动。有时agent甚至可能因纯粹的不幸而死亡,而没办法解释。
实验发现,通过在较高 τ \tau τ值的游戏环境中训练出来的agent,在通常的游戏环境中变现更好。(这也很好理解,在更复杂的、更具随机性的枪林弹雨环境中训练出来的agent当然在普通的环境中表现更优异。)实际上,增大 τ \tau τ值有助于防止agent利用到虚拟游戏环境中的BUG,这一点我们会在下面详细讨论。
4.4 将游戏策略迁移至真实游戏环境中
我们将在虚拟环境中训练的agent,放在真实场景中测试了它的性能。100盘随机连续游戏的分数是1100个step,远远超过要求的750个step的分数,也远高于在更困难的虚拟环境中获得的分数。下图是利用VAE模型对真实环境的重构结果。

我们看到,即使V模型不能正确地捕获每个帧的所有细节,例如,获得正确的怪物数量,agent仍然能够使用所学的策略在真实游戏环境中生存。由于虚拟环境一开始甚至无法跟踪怪物的确切数量,一个能够在有大量噪声和不确定的虚拟“噩梦”环境中生存的agent将在原始的、更干净的环境中“茁壮成长”(所谓的What doesn’t kill you make you stronger!)。
4.5 世界模型的欺骗实验
在我们童年的时候,我们可能会遇到一些开发电子游戏的方法,而这些方式并不是最初的游戏设计者想要的。玩家发现了收集无限生命或健康的方法,通过利用这些BUG或秘籍,他们可以轻松地完成一场本来就很困难的游戏。然而,在这样做的过程中,他们可能已经失去了学习游戏设计者所期望的掌握游戏所需技能的机会。
例如,在我们最初的实验中,我们注意到agent发现了一种对抗性策略,使得在这个由M模型控制的虚拟环境中的怪物在rollout时从不射出一个火球。即使有火球形成的迹象,agent也会以某种方式移动然后神奇地熄灭火球,就好像它在环境中有超能力一样。
因为我们的世界模型只是环境的近似概率模型,它偶尔会产生不符合实际环境规律的游戏帧序列(或称轨迹,trajectory)。正如我们之前所看到的,即使是在房间另一边的怪物数量在实际环境中也没有被世界模型完全复制出来。就像一个孩子知道空中的物体通常会落在地上一样,孩子们也会想象一些不现实的超级英雄飞过天空。因此,即使在实际环境中不存在这样的漏洞,我们的世界模型也会被controller 利用。
由于我们使用M模型为agent生成一个虚拟环境,我们也让controller能对M的所有隐藏状态 h t h_t ht的访问。这实际上是允许我们的agent访问游戏引擎的所有内部状态和内存,而不仅仅是玩家看到的游戏观察。因此,Agent可以有效地探索如何直接操纵游戏引擎的隐藏状态,从而使其期望的累积报酬最大化。这种在学习动态模型中学习策略的方法的缺点是,Agent 可以很容易地找到一个可以欺骗我们的动态模型的对抗性策略-它会在我们的动力学模型中找到一个看起来很好的策略,但是在实际环境中会失败,通常是因为它访问了模型错误的状态,因为它们远离了训练集的概率分布。
下图就是在虚拟环境中,agent通过特殊的移动方式,让房间对面的怪物一个火球也不发射。即使发射了,也有办法令火球消失。

这一弱点可能是许多以前学习RL环境的动态模型实际上并没有使用这些模型来完全替代实际环境的原因。与文中提出的M模型一样,动力学模型是一个确定性的模型,如果模型不完善,那么该模型很容易被Agent利用。使用贝叶斯模型,如PILCO,有助于在一定程度上解决这一问题的不确定性估计,但他们没有完全解决问题。最近的工作将基于模型的方法与传统的无模型RL训练结合起来——首先使用所学的策略初始化策略网络,但随后必须依赖无模型方法在实际环境中微调此策略。
在 L e a r n i n g T o T h i n k Learning\ To\ Think Learning To Think中,RNN M模型并不总是一个可靠的预测器,这是可以接受的。(基于进化策略的)RNN C模型原则上可以学会忽略一个有缺陷的M模型,或者利用M的某些有用的部分来进行任意的计算目的,包括层次规划等。但这不是我们在本文所做的——我们目前的方法仍然更接近于一些较老的系统,其中使用RNN m一步地进行预测和规划。然而,与早期的工作不同,我们使用进化算法优化Controller(就像在 L e a r n i n g T o T h i n k Learning\ To\ Think Learning To Think一样),而不是传统的RL与RNN相结合的方法,后者具有简单性和通用性的优点。
为了使我们的C模型更难利用M模型的不足,我们选择使用MDN-RNN作为动力学模型,它模拟实际环境中可能的结果的分布,而不仅仅是预测一个确定性的未来。即使实际环境是确定性的,MDN-RNN实际上也会将其近似为随机环境。这样做的好处是,我们可以在任何环境的更随机版本中训练我们的C模型——我们可以简单地调整温度参数 τ \tau τ来控制M模型中的随机性,从而控制现实性和可开发性之间的权衡。
(这段话的前几句不是很理解)Using a mixture of Gaussian model may seem like overkill given that the latent space diagonal Gaussian distribution。然而,混合密度模型中的离散模式对于具有随机离散事件的环境是有用的,诸如怪物是否决定发射火球或停留。虽然单个对角高斯分布可能足以对各个帧进行编码,但是具有MDN的RNN使得在具有离散随机状态的更复杂的环境之后更容易建模逻辑。
例如,如果我们将温度参数设置为 τ = 0.1 \tau=0.1 τ=0.1,一个很低的值,有效地用一个几乎与确定性LSTM相同的M模型来训练我们的C模型,那么这个虚拟环境中的怪物无论做什么都不能发射火球,因为mode collapse。在高斯混合模型中,M模型不能跳转到另一模式,即形成火球和发射。不管在这个虚拟环境里学到了什么策略,agent大多数时候都能获得2100分的满分,但一旦被释放到现实世界的严酷现实中,甚至连random policy都不如。
然而,请再次注意, L e a r n i n g T o T h i n k Learning\ To\ Think Learning To Think中的更简单和更鲁棒的方法并不坚持使用M模型 step by step planning。相反,Controller可以学习将M模型的subroutines(M的权重矩阵的一部分)用于任意计算目的,但也可以在M无用时和忽略M能有更好的performance时学会忽略M模型。然而,至少在我们目前的C-M变体中,M的对未来状态的预测对于训练C模型是必不可少的,这更像一些早期的C-M系统,但我们的工作与进化算法或黑箱优化相结合了。
通过将温度 τ \tau τ作为M模型的一个可调参数,我们可以看到在不同不确定度的虚拟环境中训练C模型的效果,以及这些策略如何转移到实际环境中。我们实验了改变虚拟环境的温度,并观察到在给定温度下,在虚拟环境中训练Agent之后,在实际环境中测试100次的平均得分:
| 温度 τ \tau τ | 虚拟环境得分 | 真实环境得分 |
|---|---|---|
| 0.10 | 2086 ± 140 2086\pm140 2086±140 | 193 ± 58 193\pm58 193±58 |
| 0.50 | 2060 ± 277 2060\pm277 2060±277 | 196 ± 50 196\pm50 196±50 |
| 1.00 | 1145 ± 690 1145\pm690 1145±690 | 868 ± 511 868\pm511 868±511 |
| 1.15 | 918 ± 546 918\pm546 918±546 | 1092 ± 556 1092\pm556 1092±556 |
| 1.30 | 732 ± 269 732\pm269 732±269 | 753 ± 139 753\pm139 753±139 |
| 随机策略 | N / A N/A N/A | 210 ± 108 210\pm108 210±108 |
| Gym Leader | N / A N/A N/A | 820 ± 58 820\pm58 820±58 |
我们看到,增加 τ \tau τ值可以提高M模型的复杂度,迫使Controller难以利用M模型的漏洞而采取对抗性策略。但是 τ \tau τ值调得太高会让agent在虚拟环境中什么都学不到,因此在实践中, τ \tau τ值是一个可以调整的超参数。 τ \tau τ值的大小还可以影响agent学到的策略。比如,尽管在 τ = 1.15 \tau=1.15 τ=1.15时分数最高,为 1092 ± 556 1092\pm556 1092±556,但是将 τ \tau τ值增大到1.30会使分数分布的方差变小,也就是说,游戏策略更加谨慎了。另外,Gym 游戏排行榜上的最佳成绩是 820 ± 58 820\pm58 820±58(论文的模型应该说超越了最佳表现)。
5. 迭代训练过程
在我们的实验中,任务相对简单,因此可以使用从随机策略收集的数据集来训练合理的世界模型。但如果任务环境变得更加复杂呢?在任何困难的环境中,只有当agent学会如何从策略上navigate through the world(navigate不好翻译,可以理解为,在状态空间中游走、运动)时,环境的部分信息才会被提供给agent可见。
对于更复杂的任务,需要迭代训练过程。我们需要我们的agent能够探索其世界,不断地收集新的观测数据,使其世界模型能够随着时间的推移而得到改善和完善。迭代训练过程如下:
- 初始化M模型C模型的参数。
- 在真实RL任务环境中Rollout N N N次。保存动作 a t a_t at和观测数据 x t x_t xt。
- 训练M模型,建模 P ( x t + 1 , r t + 1 , a t + 1 , d t + 1 ∣ x t , a t , h t ) P(x_{t+1},r_{t+1},a_{t+1},d_{t+1}|x_t,a_t,h_t) P(xt+1,rt+1,at+1,dt+1∣xt,at,ht), 训练C模型使期望reward最大化。
- 如果目标没有达成,返回(2)继续收集数据训练模型
我们已经证明,这个训练环路的一次迭代足以解决简单的任务。对于更困难的任务,我们需要在步骤2中的controller主动探索有益于改善其世界模型的环境的各个部分。一个令人兴奋的研究方向是研究如何将人工智能的好奇心和内在动机与信息寻求能力结合起来,以鼓励新的探索。特别是,我们可以在提高压缩质量的基础上增强奖励功能。
在目前的方法中,由于M模型是一个MDN-RNN,它为下一个帧建模一个概率分布,如果它做了一个很差的工作,那就意味着该agent已经遇到了它不熟悉的环境部分。因此,我们可以调整和重用M模型的训练损失函数来激发好奇心。通过在实际环境中翻转M模型的损失函数的符号,可以鼓励代理人探索它不熟悉的世界。它收集的新数据可能会改进世界模式。
迭代训练过程要求M模型不仅要预测下一次观测 x x x和任务是否结束的指示 d o n e done done,而且要预测下一时间的动作和奖励。对于更困难的任务来说,这可能是必需的。例如,如果agent需要学习复杂的运动技能才能在环境中行走,那么世界模型将学会模仿已经学会走路的C模型。当困难的运动技能,如步行,被吸收到一个容量大的世界模型之后,小的C模型可以依靠世界模型已经吸收的运动技能,专注于学习更高水平的技能,利用它已经学到的运动技能来控制自己。

与神经科学文献的一个有趣的联系是关于海马体经验回放的研究,它研究了当动物休息或睡觉时大脑是如何再现最近的经历的。重述最近的经历在记忆巩固中起着重要作用——依赖海马体的记忆在一段时间内独立于海马体。正如(福斯特,2017年)所言,回放(replay) l e s s l i k e d r e a m i n g a n d m o r e l i k e t h o u g h t less\ like\ dreaming\ and\ more\ like\ thought less like dreaming and more like thought,与其说是做梦,不如说是思想。我们邀请读者阅读 R e p l a y C o m e s o f A g e Replay\ Comes\ of\ Age Replay Comes of Age(福斯特,2017年),从神经科学的角度详细概述回放与理论强化学习的联系。
迭代训练可以使C-M模型发展出一种自然的分层学习方式。最近的工作关于自对弈self-play和PowerPlay也探讨了导致自然课程学习(natural curriculum learning)的方法,我们认为这是强化学习的一个更令人兴奋的研究领域。
6. 相关工作
有大量文献是关于学习一个动力学模型,并应用该动力学模型去训练一个policy的。许多概念在上世纪80年代的前馈神经网络(feed-forward neural network)中提出来,而在90年代的RNN相关研究中,又建立了 L e a r n i n g T o T h i n k Learning\ To\ Think Learning To Think的研究基础。最近的研究PILCO是一个概率的,model-based的搜索策略的方法,被设计用来解决复杂的控制问题。应用从环境中收集的data,PILCO采用高斯过程(Gaussian Process)建模系统的动力学模型,然后利用这个model采样许多状态序列,用于训练controller 完成特定的任务。
高斯过程在低维度、小规模数据上表现很好,但是难以建模长历史、高维度的观测数据。另一些最近的研究工作利用贝叶斯神经网络而不是高斯过程(GP)去学习一个动态模型,在一些状态已知、且被明确定义的低维数据的任务上表现得不错。这里我们感兴趣的是对高维的视觉数据进行动态建模,且模型的输入是原始像素帧的序列。
在机器人控制领域,仅从摄像机输入的视频信息中学习动态模型的控制是一项很有挑战意义但是也非常重要的任务。早期这方面的强化学习工作是训练一个前馈神经网络FNN,取视频序列作为输入,预测下一帧的图像。然后利用这个预测模型训练一个fovea-shifting 控制网络去寻找视觉场景下的target(最优动作?)。为了避免直接从高维数据中训练动态模型,研究人员尝试了先用神经网络学习一个高维数据的压缩表示。最近这个思路的研究已经能够利用自编码器的bottleneck层(自编码器的结构是先大后小再变大,size最小的那一层形如bottleneck,是最抽象的representation)训练一个钟摆 from pixel inputs。在压缩的表征空间中学习动态模型极大地提高了RL算法利用数据的效率。我们建议读者观看Finn的model-based RL课程 https://youtu.be/iC2a7M9voYU?t=44m35s. 了解更多的相关知识。
电子游戏环境在基于模型的RL研究中也很流行,它作为新思想的实验平台,使用前馈卷积神经网络(Cnn)来学习视频游戏的前向仿真模型(Forward Simulation Model)。学习预测不同的行为如何影响环境中的未来状态对于训练agent是有用的,因为如果agent能够预测未来发生的事情,考虑到它当前的状态和行为,它就可以简单地选择适合它的目标的最佳行动。这不仅在早期的工作中得到了证明(当时的计算成本是现在的一百万倍),而且最近对几个竞争的vizdoom环境的研究也证明了这一点。
以上工作使用FNN对下一个视频帧进行预测。我们可能希望使用能够捕获长期依赖关系的模型。RNN是一种适用于序列建模的强大模型。在一个名为“Hallucination with RNN”的讲座中,Graves展示了RNN学习Atari游戏环境的概率模型的能力。他训练RNN来学习游戏的结构,然后证明他们可以自己模拟相似的游戏水平。
早在1990年,人们就已经在一篇名为 M a k i n g t h e W o r l d D i f f e r e n t i a b l e Making the World \ Differentiable MakingtheWorld Differentiable的论文中探讨了利用RNN开发内部模型来解释未来的问题,并在 ftp://ftp.idsia.ch/pub/juergen/ijcnn90.ps.gz. 对其进行了进一步的探讨。最近一篇名为 L e a r n i n g T o T h i n k i n g Learning\ To\ Thinking Learning To Thinking的论文提出了一个统一的框架,用于构建一个基于RNN的通用问题求解器,它可以在自己的环境(指的是虚拟环境?)中学习世界模型,并学会使用该模型对未来进行推理。随后的工作使用了基于RNN的模型来生成未来的许多帧,并将其作为一个内部模型来对未来进行推理。
在本文工作中,我们使用进化策略(ES)来训练我们的controller model,因为它提供了许多好处。例如,我们只需要为ES优化器提供最终的累积奖励,而不需要整个历史。ES也很容易并行化,我们开很多core并行计算多个rollout,并快速并行地计算一组累积奖励。最近的工作证实了ES是许多很强的baseline上传统深度RL方法的一个可行的替代方案。
在深度强化学习火起来之前,进化算法已经展现出了解决强化学习问题的高效性——它能够从高维数据中学习复杂的RL任务。最近更多的工作是将VAE和ES相结合,这和我们的工作很相似。
7. 讨论和总结
我们已经证明了训练一个智能体agent完全在其模拟的潜空间梦想世界中学习和执行强化学习任务的可能性。这种方法提供了许多实际好处。例如,运行计算密集型的游戏引擎需要使用大量的计算资源将游戏状态呈现为图像帧,或者计算与游戏不是直接相关的物理环境。我们可能不想在实际环境中浪费训练agent的时间,而是希望在它的模拟环境中训练该agent。在现实世界中训练agent的成本甚至更高,因此逐步训练以实现对真实环境模拟的世界模型World Model很可能对于将policy(从world model)迁移回真实环境是非常有帮助的。我们的工作对 s i m 2 r e a l sim2real sim2real也是一个补充。
此外,我们还可以利用深度学习框架,在分布式环境中使用GPU加速我们的世界模型模拟。将世界模型实现为一个完全可微的递归计算图的好处还意味着我们可以直接在“梦”中训练agent,使用反向传播算法对其策略进行微调,使目标函数最大化。
选择使用VAE作为V模型并将其训练为独立模型也有其局限性,因为它可能编码与任务无关的部分观测结果。毕竟,根据定义,无监督学习不可能知道什么是对手头的任务是有用的。例如,在VizDoom环境中,它感知到了在墙壁上不重要的砖瓦图案,但却未能在CarRacing环境中感知到与任务相关的路上的砖头。通过与预测reward的M模型一起进行训练,VAE可能学会专注于图像中与任务相关的区域,但这里的折衷之处在于,我们可能无法重用当前的VAE model来执行新任务而不需重新训练。
学习task-relevant特征也与神经科学有关联。当得到奖励时,初级感觉神经元就会从抑制中释放出来,这意味着他们通常学习的是与任务相关的特征,而不仅仅是任何特征,(这一现象)至少在成年后是如此。
另一个令人关切的问题是我们的World Model能力有限。虽然现代存储设备可以存储使用迭代训练过程生成的大量历史数据,但我们的基于LSTM的世界模型可能并不能在网络内部的参数中记录下所有的数据信息。然而人类的大脑却可以记忆数十年甚至一个世纪的记忆。通过反向传播训练的神经网络具有很有限的容量并且受到诸如灾难性遗忘之类的问题的影响。未来的工作可能会探索替代小型MDN-RNN模型的大容量模型方案,或者是与一个外置记忆模块进行整合,如果希望感知到更复杂的世界模型的话。
就像早期的基于RNN的C-M系统,我们的世界模型在时间轴上一步一步地模拟(或者说,建模、预测)未来可能情况。我们的模型没有利用人类的分级规划(hierarchical planning)、抽象推理能力,因而经常忽略一些不相关的时空域细节信息。然而,一种更general的方法 L e a r n i n g T o T h i n k Learning\ To\ Think Learning To Think (Schmidhuber, J. On learning to think: Algorithmic information theory for novel combinations of reinforcement learning controllers and recurrent neural world models. ArXiv preprint, 2015a. https://arxiv.org/abs/1511.09249. 没读过这篇,猜与元学习Meta Learning有关)则不会收到上述这种比较原始的方法所限。它的模型中有一个循环C模型(Recurrent C),用于学习处理recurrent M模型的subroutine,并且reuse them(指subroutines) for problem solving in arbitrary computable ways,比如 through hierarchical planning or other kinds of exploiting parts of M’s program-like weight matrix.(不是很懂在说什么)。一个最近的工作是 O n e B i g N e t One\ Big\ Net One Big Net,作为C-M模型的推广,它把C模型和M模型拆解成小型网络,并使用PowerPlay-like behavioural replay(教师网络被压缩成学生网络)以避免在学习新的控制策略时忘记了旧的知识和策略。关于这些更general的方法将会在之后进行实验。
A. 附录
在这一部分,我们将对模型的细节和训练的细节展开叙述。
A.1 变分自编码器 Variational Autoencoder
论文中采用的是卷积变分自编码器,作为总体模型中的V模型。不像普通的自编码器一样,enforcing a Gaussian prior over the latent vector z z z also limits the amount of information capacity for compressing each frame, but this Gaussian prior also makes the world model more robust to unrealistic z z z vectors generated by the M Model.(这句话不是很理解,大致意思是说,VAE模型将“先验高斯分布”压缩到潜层向量 z z z之后,会丢失一些信息,但是也会给模型带来一些鲁棒性,比如面对虚拟环境产生的不真实 z z z向量的时候。)

当游戏环境给出了原始高维图像,模型首先将图像resize到 64 × 64 × 3 64\times64\times3 64×64×3的彩色图像,这个三通道矩阵的每个元素都是 [ 0 , 1 ] [0,1] [0,1]的实数。随后 64 ∗ 64 ∗ 3 64*64*3 64∗64∗3的input tensor经过4个卷积层,最终处理成两个等长向量 μ \mu μ 和 σ \sigma σ,向量长度都是 N c N_c Nc 。潜层向量 z z z 就是从高斯先验分布 N ( μ , σ I ) N(\mu,\sigma I) N(μ,σI)中采样得来的。(PS:这里的 σ I \sigma I σI 感觉是一个对角矩阵,主对角元素是 σ \sigma σ 的各个分量,因为 z z z是一个向量,向量的每一维服从独立的高斯分布,所以协方差矩阵是一个对角矩阵,但是 σ I \sigma I σI 的写法有点问题,因为 I I I 一般表示单位矩阵, σ \sigma σ 和 I I I 做矩阵乘法还是 σ \sigma σ本身。)在CarRacing游戏中, N c = 32 N_c=32 Nc=32,在VizDoom游戏中等于 64 64 64。随后潜层向量经过四个反卷积网络,重构原图像。
每个卷积和反卷积的滑动步长是 s t r i d e = 2 stride=2 stride=2,上图中斜体的文字分别表示这一层的激活函数、卷积/反卷积操作、卷积核的数量(通道数)、卷积核的尺寸(注意,卷积操作之间没有池化操作),除了输出层用sigmoid激活函数之外,其它层都用ReLU激活函数,因为最后的输出层输出的是像素值大小,所以需要其分布在 [ 0 , 1 ] [0,1] [0,1]之间。VAE模型只用random policy收集的数据训练1个epoch。损失函数有两部分组成,一部分是原图像与重构图像的重构误差,用 L 2 L^2 L2距离来衡量,另一部分是KL散度损失(谁和谁的KL散度?原图和重构图的KL散度?)
A.2 循环神经网络
对于M模型,我们用长短时记忆网络(LSTM)加上混合密度网络(Mixture Density Network)作为输出层。我们用这样的网络去建模下一个状态 z z z的概率分布,这个概率分布是用若干个高斯分布去估计的。这个方法和在无条件约束的手写字生成领域的Grave的 https://arxiv.org/abs/1308.0850. 这篇文章很相似,和SketchRNN的解码器部分也很类似。唯一的不同就是我们的方法没有没有去建模 z z z和 z z z之间的相关系数 ρ \rho ρ ,而是生成了factored Gaussian Distribution的对角协方差矩阵。(关于MDN的相关知识,可以看我的另一篇文章: X X X X X X X X X X X X X X X X X X X X X X XXXXXXXXXXXXXXXXXXXXXX XXXXXXXXXXXXXXXXXXXXXX)

不像SketchRNN和手写字生成的任务一样,需要用MDN-RNN模型生成下一笔画的概率密度函数,本文使用的MDN-RNN模型是用来生成下一个潜层向量 z z z的PDF(Probability Density Function)的。我们随后从这个概率密度函数中采样,生成(预测)下一step的虚拟环境(hallucinated environment)。在VizDoom游戏中,我们也用来预测agent在下一个step死亡的概率,如果这个概率大于50%,就设定游戏结束(当然是虚拟的游戏环境中)。我们已知每个time step下,death是一个小概率的事件,我们就得到一个更稳定的截断法(cutoff approach,不是很理解),相比于从伯努利分布中采样的话。
MDN-RNN模型用随机策略玩游戏收集的数据训练20个epoch。在CarRacing游戏中,LSTM有256个隐层单元(Hidden Unit),而在VizDoom游戏中,用到了512个hidden units。对这两个游戏task,我们都采用5个高斯分布混合得到最终 z z z的PDF,但是没有建模相关系数 r h o rho rho ,因此 z z z是从a factored mixture of Gaussian distribution中采样得到的(不是很理解其中的因果关系?)
下面一段话也不是很理解,感兴趣的朋友可以在评论区交流一下。 When training the MDN-RNN using teacher forcing from the recorded data, we store a pre-computed set of μ \mu μ and σ \sigma σ for each of the frames, and sample an input z ~ N( μ \mu μ, σ \sigma σ) each time we construct a training batch, to prevent overfitting our MDN-RNN to a specific sampled z z z.
A.3 Controller Model
在CarRacing游戏和VizDoom游戏中,我们都使用了 t a n h tanh tanh函数作为限制动作空间的非线性函数(因为tanh函数的值域是 [ − 1 , 1 ] [-1,1] [−1,1],且对绝对值很大的输入有抑制作用)。比如,在CarRacing中,方向盘的变化范围是 [ − 1 , 1 ] [-1,1] [−1,1],油门的范围是 [ 0 , 1 ] [0,1] [0,1],刹车的范围是 [ 0 , 1 ] [0,1] [0,1]。再比如在VizDoom中,我们将离散的动作转换成连续的动作空间,范围是 [ − 1 , 1 ] [-1,1] [−1,1],并将这个区间分成三份,左边一份 [ − 1 , − 1 3 ] [-1,-\frac13] [−1,−31]表示向左移动,中间的 ( − 1 3 , 1 3 ) (-\frac13,\frac13) (−31,31)表示agent保持不动,右边的 [ 1 3 , 1 ] [\frac13,1] [31,1]表示向右移动。
在CarRacing中,给controller model的输出是 z z z和 h t h_t ht,而在VizDoom中,除了 z z z和 h t h_t ht还要cell vector c c c
(我估计这个cell vector就是预测是否死亡的概率变量)。
A.4 进化算法
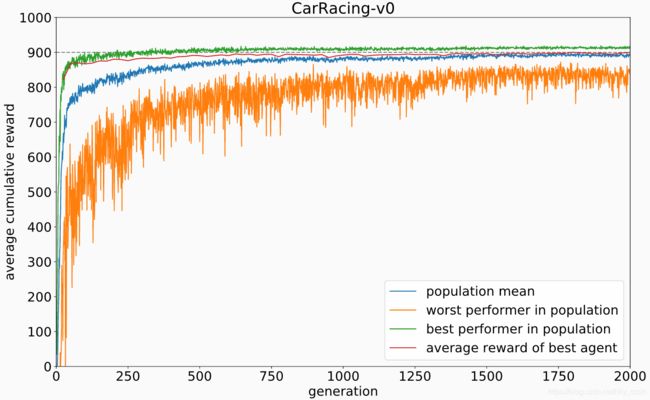
论文中使用协方差矩阵自适应进化策略(Covariance-Matrix Adaptation Evolution Strategy,CMA-ES,https://arxiv.org/abs/1604.00772.) 来优化controller model的参数。论文使用的应该是CMA-ES的改进版,叫做Evolving Stable Strategies,参考网址是 http://blog.otoro.net/2017/11/12/evolving-stable-strategies/。进化种群的规模是64,也就是初始化64个controller agent,相当于遗传算法中的64个个体,或者粒子群算法中的64个粒子。令每个controller agent 随机玩游戏16次,累计回报的平均值就作为优化的目标(或者说,进化算法中的适应度函数,fitness value)。下面的图显示了最优秀、最差的个体的fitness value随进化代数的曲线,以及种群的平均performance。
因为实验的目标是找到一个智能体,在平均水平上达到900分(CarRacing游戏),所以每过25次进化,就选取种群中最好的个体,令其进行1024盘游戏,记录其平均得分,也就是上图的红线。经过1800代进化,最优秀的agent在1024盘游戏上已经达到900.46的平均分数。之所以要测试1024盘游戏,而不是100盘游戏,是因为算法的一开始设置好了每个CPU核心跑16个rollout,一共64个core,所以比较高效。
另外,我们还画了同一个controller agent玩100盘游戏的得分直方图。分数是 906 ± 21 906\pm 21 906±21。
我们同样也实验了只利用 z z z向量,而不利用 h t h_t ht来玩游戏的controller agent的测试表现。测试分两个方案。第一个方案,controller直接将 z z z线性映射到动作空间 a a a;第二种方案,在 z z z和 a a a之间加入了40个 t a n h tanh tanh的单隐层网络,将controller的参数增加到1443,使其与最初版本更具对比性。
下面第一个图是方案1,平均得分 632 ± 251 632\pm251 632±251,第2个图是加入单隐层的方案2,平均得分 788 ± 141 788\pm141 788±141。
A.5 DoomRNN
我们在VizDoom游戏上也做了个相似的实验,只不过,如上文所述,实验是跑在RNN虚拟出来的VizDoom游戏环境上的。**需要注意的是,论文中并没有在真实的VizDoom环境中训练agent,而只是用random policy在真实环境中收集数据,训练MDN-RNN,然后用训练好的MDN-RNN在隐层空间来模拟游戏环境,并在这个环境中训练controller。**在隐空间中训练有以下几个好处。1、计算更高效,不需要可视化游戏画面,只需在latent space中运算即可;2、MDN-RNN可以模拟真实游戏环境的输出,因此也不需要启动真正的游戏environment,也节省了算力。

在虚拟的,由RNN生成的VizDoom环境中,我们稍微调高温度参数 τ \tau τ的值, τ = 1.15 \tau=1.15 τ=1.15(文章中应该没有说明白 τ \tau τ是如何具体控制模型表现的?),以使agent在一个更具挑战性的、难度更高的虚拟环境中学习。最优秀的agent在1024盘游戏中获得 959 959 959的分数,也就是上图中的红线。令这个最好的agent在真实环境中测试,得到的分数是 1092 ± 556 1092\pm556 1092±556,游戏盘数100盘。