人工智能直通车系列24【机器学习基础】（机器学习模型评估指标（回归））

目录

机器学习模型评估指标（回归）

1. 均方误差（Mean Squared Error, MSE）

2. 均方根误差（Root Mean Squared Error, RMSE）

3. 平均绝对误差（Mean Absolute Error, MAE）

4. 决定系数（Coefficient of Determination, R2）

---

机器学习模型评估指标（回归）

1. 均方误差（Mean Squared Error, MSE）

• 详细解释
  • 均方误差是回归问题中最常用的评估指标之一。它计算的是预测值与真实值之间误差的平方的平均值。公式为：
    
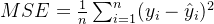
    其中，是样本数量， 是第个样本的真实值， 是第  个样本的预测值。
  • MSE 对较大的误差给予了更大的惩罚，因为误差是平方的。这意味着模型在预测时出现较大的偏差会导致 MSE 显著增大。MSE 的值越小，说明模型的预测效果越好。
• 场景示例

import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_regression

# 生成回归数据集
X, y = make_regression(n_samples=100, n_features=1, noise=0.5, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 训练线性回归模型
model = LinearRegression()
model.fit(X_train, y_train)

# 进行预测
y_pred = model.predict(X_test)

# 计算均方误差
mse = mean_squared_error(y_test, y_pred)
print(f"均方误差 (MSE): {mse}")

2. 均方根误差（Root Mean Squared Error, RMSE）

• 详细解释
  • 均方根误差是均方误差的平方根，公式为：
    
  • RMSE 的优点是它的单位与目标变量的单位相同，这使得它在解释模型的误差大小时更加直观。与 MSE 类似，RMSE 越小，模型的预测效果越好。
• 场景示例

import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_regression

# 生成回归数据集
X, y = make_regression(n_samples=100, n_features=1, noise=0.5, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 训练线性回归模型
model = LinearRegression()
model.fit(X_train, y_train)

# 进行预测
y_pred = model.predict(X_test)

# 计算均方根误差
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
print(f"均方根误差 (RMSE): {rmse}")

3. 平均绝对误差（Mean Absolute Error, MAE）

• 详细解释
  • 平均绝对误差计算的是预测值与真实值之间绝对误差的平均值，公式为：
    
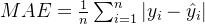
  • 与 MSE 不同，MAE 对所有的误差给予了相同的权重，不会对较大的误差进行过度惩罚。因此，MAE 对异常值的敏感性相对较低。MAE 的值越小，模型的预测效果越好。
• 场景示例

import numpy as np
from sklearn.metrics import mean_absolute_error
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_regression

# 生成回归数据集
X, y = make_regression(n_samples=100, n_features=1, noise=0.5, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 训练线性回归模型
model = LinearRegression()
model.fit(X_train, y_train)

# 进行预测
y_pred = model.predict(X_test)

# 计算平均绝对误差
mae = mean_absolute_error(y_test, y_pred)
print(f"平均绝对误差 (MAE): {mae}")

4. 决定系数（Coefficient of Determination, ）

• 详细解释
  • 决定系数衡量了模型对数据的拟合程度，它表示模型能够解释的因变量的变异比例。公式为：
    
    其中，是真实值的平均值。
  •  的取值范围是 (。 表示模型完美拟合数据，即预测值与真实值完全一致；表示模型的预测效果与简单地使用平均值进行预测相同； 为负数表示模型的预测效果比使用平均值进行预测还要差。
• 场景示例

import numpy as np
from sklearn.metrics import r2_score
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_regression

# 生成回归数据集
X, y = make_regression(n_samples=100, n_features=1, noise=0.5, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 训练线性回归模型
model = LinearRegression()
model.fit(X_train, y_train)

# 进行预测
y_pred = model.predict(X_test)

# 计算决定系数
r2 = r2_score(y_test, y_pred)
print(f"决定系数 (R^2): {r2}")

这些评估指标从不同的角度衡量了回归模型的性能，在实际应用中，我们通常会综合使用多个指标来全面评估模型的优劣。