《异常检测——从经典算法到深度学习》19 OmniAnomaly：基于随机循环网络的多元时间序列鲁棒异常检测

《异常检测——从经典算法到深度学习》

• 0 概论

• 1 基于隔离森林的异常检测算法

• 2 基于LOF的异常检测算法

• 3 基于One-Class SVM的异常检测算法

• 4 基于高斯概率密度异常检测算法

• 5 Opprentice——异常检测经典算法最终篇

• 6 基于重构概率的 VAE 异常检测

• 7 基于条件VAE异常检测

• 8 Donut: 基于 VAE 的 Web 应用周期性 KPI 无监督异常检测

• 9 异常检测资料汇总（持续更新&抛砖引玉）

• 10 Bagel: 基于条件 VAE 的鲁棒无监督KPI异常检测

• 11 ADS: 针对大量出现的KPI流快速部署异常检测模型

• 12 Buzz: 对复杂 KPI 基于VAE对抗训练的非监督异常检测

• 13 MAD: 基于GANs的时间序列数据多元异常检测

• 14 对于流数据基于 RRCF 的异常检测

• 15 通过无监督和主动学习进行实用的白盒异常检测

• 16 基于VAE和LOF的无监督KPI异常检测算法

• 17 基于 VAE-LSTM 混合模型的时间异常检测

• 18 USAD：多元时间序列的无监督异常检测

• 19 OmniAnomaly：基于随机循环网络的多元时间序列鲁棒异常检测

• 20 HotSpot：多维特征 Additive KPI 的异常定位
  相关：

• VAE 模型基本原理简单介绍

• GAN 数学原理简单介绍以及代码实践

• 单指标时间序列异常检测——基于重构概率的变分自编码（VAE）代码实现（详细解释）

19. 基于随机循环网络的多元时间序列鲁棒异常检测

论文下载：netman
源码地址：github
数据集：https://s3-us-west-2.amazonaws.com/telemanom/data.zip
数据集对应的标签：https://raw.githubusercontent.com/khundman/telemanom/master/labeled_anomalies.csv

19.1 论文概述

OmniAnomaly是一种将门控递归单元（GRU）和变分自动编码器（VAE）相结合的随机递归神经网络模型，其核心思想是学习多元时间序列的正态模式，并利用重构概率进行异常判断。

可以概括为以下几个关键字：

• 多元时间序列数据；适用的数据类型。
• RNN，循环神经网络。
• VAE，变分自编码。
• VAE 使用重构概率进行异常检测。
• 算法具有良好的鲁棒性。

接下来我们关注一下论文的 contribution。

• 提出了一种新的随机循环神经网络 OmniAnomery，用于多变量时间序列的异常检测。 OmniAnomery 是第一个多元时间序列异常检测算法，它能够处理随机变量之间显式的时间相关性，以学习工业设备监控所需的输入数据的鲁棒性复现。
• 我们提出了第一个异常解释方法，用于基于随机的多元时间序列异常检测算法，该算法不仅适用于OmniAnomery，还适用于其他算法，如[16]。 全异常解释精度可达0.89。
• 实验表明 OmniAnomaly 的异常阈值自动选择效果比 GRU, planar NF, stochastic variable connection 和 adjusted Peaks-Over-Threshold 方法更好。
• 通过大量的实验，我们发现OmniAntory在三个真实数据集中的 F1-score 为0.86，效果优良且鲁棒性更好。
• 为了更好地重现本文的结果，我们在GitHub1上公开发布了我们的代码和服务器实验数据集。

这部分 contribution 读起来多少有些不适，重新概括大概为：

• 是一个基于随机循环神经网络、应用于多元时间序列异常检测的算法；
• 对于三个真实数据进行实验，F1-score 优于其他现有算法；
• 具有很好的异常阈值自动选择方法。

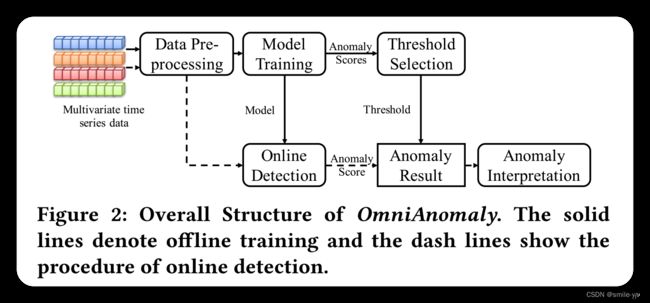
了解大概内容以后，再看一下论文的总体结构：

大致过程可以概述为：

1. 输入多元时间序列数据；
2. 预处理后得到训练集与测试集；
3. 训练集送去训练，测试集送去测试（训练后再开始测试）
4. 自动选择异常阈值
5. 根据异常阈值，检测器对异常分数进行处理，输出异常判定结果。

接下来看一下论文的具体内容，为了快速抓住重点，加速阅读，我们跳过那些作用不大的背景描述，直接看一些重要部分吧。

19.2 相关技术背景介绍（GRU / VAE / Planar NF）

对应原文中的 3.3 节

• GRU (Gated Recurrent Unit) ：门控循环神经⽹络（Gated Recurrent Neural Network）是一种 RNN，它通过可以学习的⻔来控制信息的流动。而 门控循环单元（Gated Recurrent Unit，GRU）是⼀种常⽤的门控循环神经⽹络。论文中应用GRU来捕捉时间序列中复杂的时间相关性。

• VAE (Variational Auto-Encoder) ：一种深度贝叶斯模型，它通过使用低维度的隐藏层来重构输入数据。从输入数据到隐藏层的过程称为 变分网络（Inferance Network） ，从隐藏层到重构数据的过程称为 生成网络（Generative Network）。

• SGVB (Stochastic Gradient Variational Bayes) : 随机梯度变分贝叶斯，是一种变分推理算法，常常用在 VAE 中，来训练参数 $\varphi$ 和 $\theta$ 使得 ELBO (Evidence Lower Bound，记作 $\mathcal{L}(x_t)$ ) 最大化。

  关于 VAE，我们介绍了很多很多次，可以参考 VAE 模型基本原理简单介绍。

其中 ELBO 的表达式为

$$\begin{array}{rl}\mathcal{L}\left({\mathbf{x}}_{\mathbf{t}}\right)& ={\mathbb{E}}_{q_{\varphi }\left({\mathbf{z}}_{\mathbf{t}}|{\mathbf{x}}_{\mathbf{t}}\right)}\left[\log \left(p_{\theta }\left({\mathbf{x}}_{\mathbf{t}}|{\mathbf{z}}_{\mathbf{t}}\right)\right)\right]-D_{KL}\left[q_{\varphi }\left({\mathbf{z}}_{\mathbf{t}}|{\mathbf{x}}_{\mathbf{t}}\right)||p_{\theta }\left({\mathbf{z}}_{\mathbf{t}}\right)\right]\\ & ={\mathbb{E}}_{q_{\varphi }\left({\mathbf{z}}_{\mathbf{t}}|{\mathbf{x}}_{\mathbf{t}}\right)}\left[\log \left(p_{\theta }\left({\mathbf{x}}_{\mathbf{t}}|{\mathbf{z}}_{\mathbf{t}}\right)\right)+\log \left(p_{\theta }\left({\mathbf{z}}_{\mathbf{t}}\right)\right)-\log \left(q_{\varphi }\left({\mathbf{z}}_{\mathbf{t}}|{\mathbf{x}}_{\mathbf{t}}\right)\right)\right]\end{array}\text{\hspace{1em}(1)}$$

蒙特卡罗积分（Monte Carlo integration）是一种变分推理算法，可以用来计算公式 1 中的均值，如公式 2 所示，其中，$z_{\mathbf{t}}^{(l)}$ 是从 $q_{\varphi }\left({\mathbf{z}}_{\mathbf{t}}|{\mathbf{x}}_{\mathbf{t}}\right)$ 第 $l$ 次的采样结果。:

$$\mathcal{L}\left({\mathbf{x}}_{\mathbf{t}}\right)\approx \frac{1}{L}\sum _{l=1}^L\left[\log \left(p_{\theta }\left({\mathbf{x}}_{\mathbf{t}}|{\mathbf{z}}_{\mathbf{t}}^{(l)}\right)\right)+\log \left(p_{\theta }\left({\mathbf{z}}_{\mathbf{t}}^{(l)}\right)\right)-\log \left(q_{\varphi }\left({\mathbf{z}}_{\mathbf{t}}^{(l)}|{\mathbf{x}}_{\mathbf{t}}\right)\right)\right]\text{\hspace{1em}(2)}$$

在变分网络 $qnet$ 中，$q_{\varphi }\left({\mathbf{z}}_{\mathbf{t}}|{\mathbf{x}}_{\mathbf{t}}\right)$ 常假定为对角高斯 (diagonal Gaussian)，但是，这个简单的假设会使网络欠拟合 ，因为 $q_{\varphi }\left({\mathbf{z}}_{\mathbf{t}}|{\mathbf{x}}_{\mathbf{t}}\right)$ 可能不一定遵循高斯分布。为了学习非高斯后验密度 $q_{\varphi }\left({\mathbf{z}}_{\mathbf{t}}|{\mathbf{x}}_{\mathbf{t}}\right)$ ，文献 [18,Variational Inference with Normalizing Flows] 提出了一种利用可逆映射对 $q_{\varphi }\left({\mathbf{z}}_{\mathbf{t}}|{\mathbf{x}}_{\mathbf{t}}\right)$ 进行变换的方法 planar NF。

论文首先从 $q_{\varphi }\left({\mathbf{z}}_{\mathbf{t}}|{\mathbf{x}}_{\mathbf{t}}\right)$ 采样得到 $z_{\mathbf{t}}^0$，然后通过一个可逆映射链得到 $z_{\mathbf{t}}^{\mathbf{K}}=f^K\left(f^{K-1}\left(\dots f^1\left({\mathbf{z}}_{\mathrm{t}}^0\right)\right)\right)$，其中 $f^k(k=1,2...K)$ 是可逆映射函数 $(f^k\left({\mathrm{z}}_{\mathrm{t}}^{\mathrm{k}-1}\right)={\mathrm{z}}_{\mathrm{t}}^{\mathrm{k}-1}+\mathrm{u}\tanh \left({\mathbf{w}}^{\mathrm{T}}{\mathrm{z}}_{\mathrm{t}}^{\mathrm{k}-1}+\mathrm{b}\right)$，其中 $\mathbf{u},\mathbf{w},\mathbf{b}$ 是文献 [18] 中的参数。在 $qnet$ 中，我们只把planar NF 的最终输出 $z_t^K$，作为隐藏层的随机变量 $z_t$（即 $z_t=z_t^K$）。

19.3 算法设计

19.3.1 算法总体结构

OmniAnomaly的基本思想如下：

• 首先，它使用GRU来捕捉 x 空间中多变量观测之间复杂的时间依赖性。
• 其次，我们应用一种流行的重构学习变分算法 VAE，将观测（即 x 空间中的输入观测）映射到随机变量（即 z 空间）。
• 第三，受语音重构文献[5，Sequential neural models with stochastic layers] 的启发，为了在空间中显式建模随机变量之间的时间依赖性，我们提出了随机变量连接技术（线性高斯状态空间模型(Linear Gaussian State Space Model，SSM)[8，Linear Gaussian State Space Modeling] 连接随机变量之间，随机变量与 GRU 隐变量的串联）。
• 第四， 为了让 $qnet$ 中的随机变量捕获输入数据的复杂分布，我们采用 planar NF[18]，它使用一系列可逆映射来学习隐藏随机空间中的非高斯后验分布。

OmniAnomaly 模型的概览图，其中左边是指 $qnet$ 变分网络，右边是指 $pnet$ 生成网络。

这个结构图片是真的真的不好看……

这个图片类比一下我们在 Donut 和 Bagel 算法中的模型，总体结构是一样的，需要注意 GRU 的添加。

接下来看看是怎么计算，对应着上面的图片进行学习。

其中使用 $t$ 时刻的观测数据 $x_t$，以及 GRU 中 $t-1$ 时刻的隐变量 $e_{t-1}$，生成 GRU 中 $t$ 时刻的隐变量 $e_t$，其中的对应关系如下公式 (3a) 所示。同样地，对于 VAE 中 $\mu$ 和 $\sigma$ 在 $t$ 时刻与隐变量 $z_t$ 的对应关系如 公式 (3b) (3c) 所示。

$${\mathbf{e}}_{\mathrm{t}}=\left(1-{\mathrm{c}}_{\mathrm{t}}^{\mathrm{e}}\right)\circ \tanh \left({\mathbf{w}}^{\mathrm{e}}{\mathbf{x}}_{\mathbf{t}}+{\mathbf{u}}^{\mathrm{e}}\left({\mathbf{r}}_{\mathrm{t}}^{\mathrm{e}}\circ {\mathbf{e}}_{\mathrm{t}-1}\right)+{\mathrm{b}}^{\mathrm{e}}\right)+{\mathbf{c}}_{\mathrm{t}}^{\mathrm{e}}\circ {\mathbf{e}}_{\mathrm{t}-1}\text{\hspace{1em}(3a)}$$

$${\mu }_{{\mathrm{z}}_{\mathrm{t}}}={\mathbf{w}}^{{\mathbf{\mu }}_{\mathrm{z}}}{h}^{\varphi }\left(\left[{\mathbf{z}}_{\mathrm{t}-1},{\mathbf{e}}_{\mathrm{t}}\right]\right)+{\mathbf{b}}^{{\mathbf{\mu }}_{\mathrm{z}}}\text{\hspace{1em}(3b)}$$

$${\sigma }_{{\mathrm{z}}_{\mathrm{t}}}=\mathrm{softplus}\left({\mathrm{w}}^{{\sigma }_{\mathrm{z}}}{h}^{\varphi }\left(\left[{\mathrm{z}}_{\mathrm{t}-1},{\mathbf{e}}_{\mathrm{t}}\right]\right)+{\mathrm{b}}^{{\sigma }_{\mathrm{z}}}\right)+{ϵ}^{{\sigma }_{\mathrm{z}}}\text{\hspace{1em}(3c)}$$

在公式 3a 中，${\mathbf{r}}_{\mathbf{t}}^{\mathbf{e}}$ 是决定如何将新的输入数据与前一个结合的重置门，其中 ${\mathbf{r}}_{\mathbf{t}}^{\mathbf{e}}=sigmod({\mathbf{w}}^{{\mathbf{r}}^{\mathbf{e}}}{\mathbf{x}}_{\mathbf{t}}+{\mathbf{u}}^{{\mathbf{r}}^{\mathbf{e}}}+{\mathbf{b}}^{{\mathbf{r}}^{\mathbf{e}}})$。

${\mathbf{c}}_{\mathbf{t}}^{\mathbf{e}}=\mathrm{sigmod}\left({\mathbf{w}}^{{\mathbf{c}}^{\mathrm{e}}}{\mathbf{x}}_{\mathbf{t}}+{\mathbf{u}}^{{\mathbf{c}}^{\mathrm{e}}}{\mathbf{e}}_{\mathbf{t}-1}+{\mathbf{b}}^{{\mathbf{c}}^{\mathrm{e}}}\right)$ 是决定需要保留多少以前的内存的更新门。

如图 3(b1) 所示，$[{\mathbf{z}}_{\mathrm{t}-1},{\mathbf{e}}_{\mathrm{t}}]]$ 是 ${\mathbf{z}}_{\mathbf{t}-1}$ 和 ${\mathbf{e}}_{\mathbf{t}}$ 的串联。$h^{\varphi }$ 表示带有 ReLU 激活函数的隐藏层。${\mu }_{{\mathbf{z}}_{\mathbf{t}}}$ 来源于一个线性层，${\sigma }_{{\mathbf{z}}_{\mathbf{t}}}$ 是通过带有小随机变量 $ϵ$ （以防止数值溢出）的 soft-plus 激活函数而得到的。

所有的 ${\mathbf{u}}^{\ast }-\mathbf{s}$，${\mathbf{w}}^{\ast }-\mathbf{s}$， ${\mathbf{b}}^{\ast }-\mathbf{s}$ 是相应层的参数。 ${\mathbf{z}}_{\mathbf{t}}^0$ 是 $qnet$ 的输出结果，是对角线高斯并从 $\mathcal{N}\left({\mu }_{Z_t},{\sigma }_{{\mathrm{Z}}_t}^2\mathbf{I}\right)$采样而来。 为了学习 $q_{\varphi }\left({\mathbf{z}}_{\mathbf{t}}|{\mathbf{x}}_{\mathbf{t}}\right)$ 的后验分布，我们使用 planar NF 来最大化 ${\mathbf{z}}_{\mathbf{t}}$。如图 3(b1) 所示，${\mathbf{z}}_{\mathbf{t}}$ （即 ${\mathbf{z}}_{\mathbf{t}}^{\mathbf{K}}$）是 ${\mathbf{z}}_{\mathbf{t}}^0$ 通过 planar 映射中 $K$ 次转换链 $f^k$ 而得到的。

如图3(b2)所示，$pnet$ 尝试使用类似于 $qnet$ 的结构对 $z_t$ 进行重构得到 $x_t$。 我们利用线性高斯 SSM[8] 来 “连接” $qnet$ 中的 $z$ 空间变量，并使其暂时依赖关系为 ${\mathrm{z}}_{\mathrm{t}}={\mathrm{O}}_{\theta }\left({\mathrm{T}}_{\theta }{\mathrm{z}}_{\mathrm{t}-1}+{\mathrm{v}}_{\mathrm{t}}\right)+{ϵ}_{\mathrm{t}}$ ，其中 ${\mathrm{T}}_{\theta }$ 和 ${\mathrm{O}}_{\theta }$ 是转换矩阵和观测矩阵，${\mathbf{v}}_{\mathbf{t}})$ 和 ${ϵ}_{\mathrm{t}}$ 是转换和观测噪声。 在 $t$ 时刻的 $z_t$ 和 $t-1$时刻的变量 ${\mathbf{d}}_{\mathbf{t}-1}$ ，通过GRU单元格来产生确定性变量 ${\mathbf{d}}_{\mathbf{t}}$ （公式 4a）。然后 ${\mathbf{d}}_{\mathbf{t}}$ 通过稠密层进一步处理，生成变量 KaTeX parse error: Expected group after '^' at position 10: \mathbf{x^̲'t} （${\mathbf{x}}^{\mathbf{t}}$ 的重构变量） 的均值 ${\mu }_{x_t}$ 和标准差 ${\sigma }_{x_t}$ （公式4b和公式4c）。

类似于 $qnet$，$pnet$ 可以以如下方式计算：

$${\mathbf{d}}_{\mathbf{t}}=\left(1-{\mathbf{c}}_{\mathbf{t}}^{\mathrm{d}}\right)\circ \tanh \left({\mathbf{w}}^{\mathrm{d}}{\mathrm{z}}_{\mathrm{t}}+{\mathbf{u}}^{\mathrm{d}}\left({\mathrm{r}}_{\mathrm{t}}^{\mathrm{d}}\circ {\mathbf{d}}_{\mathbf{t}-1}\right)+{\mathbf{b}}^{\mathrm{d}}\right)+{\mathbf{c}}_{\mathbf{t}}^{\mathrm{d}}\circ {\mathbf{d}}_{\mathbf{t}-1}\text{\hspace{1em}(4a)}$$

$${\mathbf{\mu }}_{{\mathrm{x}}_{\mathrm{t}}}={\mathbf{w}}^{{\mathbf{\mu }}_{\mathrm{x}}}{h}^{\theta }\left({\mathrm{d}}_{\mathrm{t}}\right)+{\mathrm{b}}^{{\mu }_{\mathrm{x}}}\text{\hspace{1em}(4b)}$$

$${\sigma }_{{\mathrm{x}}_{\mathrm{t}}}=\mathrm{softplus}\left({\mathbf{w}}^{{\sigma }_{\mathrm{x}}}{h}^{\theta }\left({\mathbf{d}}_{\mathrm{t}}\right)+{\mathbf{b}}^{{\sigma }_{\mathrm{x}}}\right)+{ϵ}^{{\sigma }_{\mathrm{x}}}\text{\hspace{1em}(4c)}$$

其中，${\mathbf{r}}_{\mathbf{t}}^{\mathbf{d}}=\mathrm{sigmod}\left({\mathbf{w}}^{{\mathbf{r}}^{\mathrm{d}}}{\mathbf{z}}_{\mathbf{t}}+{\mathbf{u}}^{{\mathbf{r}}^{\mathrm{d}}}{\mathbf{d}}_{\mathbf{t}-1}+{\mathbf{b}}^{{\mathbf{r}}^{\mathrm{d}}}\right)$ 和 ${\mathbf{r}}_{\mathbf{t}}^{\mathbf{d}}=\mathrm{sigmod}\left({\mathbf{w}}^{{\mathbf{c}}^{\mathrm{d}}}{\mathbf{z}}_{\mathbf{t}}+{\mathbf{u}}^{{\mathbf{c}}^{\mathrm{d}}}{\mathbf{d}}_{\mathbf{t}-1}+{\mathbf{b}}^{{\mathbf{c}}^{\mathrm{d}}}\right)$ 分别为复位门和更新门。

重构数据$x_t^{{}^{\prime }}$ 是从 $\mathcal{N}\left({\mu }_{{\mathbf{x}}_{\mathfrak{t}}},{\sigma }_{{\mathbf{x}}_{\mathrm{t}}}^2\mathrm{I}\right)$ 采样，并从 $z_t$ 中创建。如果$t$ 时刻存在异常，则$x_t^{{}^{\prime }}$ 可能与原始数据 $x_t$ 显著不同。 因此，我们可以基于$x_t$ 的重构概率来检测异常。

19.3.2 离线训练

$OmniAnomaly$ 中的 $pnet$ 和 $qnet$ 通过同时调整网络参数 ($u\ast -s$、$w\ast -s$ 和 $b\ast -s$ ) 进行训练。 与VAE模型类似，我们可以通过优化ELBO直接训练我们的模型，如3.3节所述。 训练数据集中的每个输入序列数据（例如 $xt-T:t）的长度为$T+1$。 对于第 $l$ 个样本 $z_{t-T:t}^{(l)}$，其中 $1\le l\le L$ , $L$ 是样本长度，损失函数可以公式化如下：

$$\begin{array}{rl}\mathcal{L}\left({\mathbf{x}}_{\mathbf{t}-\mathrm{T}:\mathrm{t}}\right)\approx \frac{1}{L}\sum _{l=1}^L& [\log \left(p_{\theta }\left({\mathbf{x}}_{\mathbf{t}-\mathrm{T}:\mathrm{t}}\mid {\mathbf{z}}_{\mathbf{t}-\mathrm{T}:\mathrm{t}}^{(l)}\right)\right)+\\ & \log \left(p_{\theta }\left({\mathbf{z}}_{\mathbf{t}-\mathrm{T}:\mathrm{t}}^{(l)}\right)\right)-\log \left(q_{\varphi }\left({\mathbf{z}}_{\mathbf{t}-\mathrm{T}:\mathrm{t}}^{(l)}\mid {\mathbf{x}}_{\mathbf{t}-\mathrm{T}:\mathrm{t}}\right)\right)]\end{array}\text{\hspace{1em}(5)}$$

对于每一个样本，公式 5 中的第一条的重构错误被忽略：$\log \left(p_{\theta }\left({\mathbf{x}}_{\mathbf{t}-\mathrm{T}:\mathrm{t}}\mid {\mathbf{z}}_{\mathbf{t}-\mathrm{T}:\mathrm{t}}\right)\right)={\sum }_{i=t-T}^t\log \left(p_{\theta }\left({\mathbf{x}}_{\mathbf{i}}\mid {\mathbf{z}}_{\mathbf{t}-\mathrm{T}:\mathbf{i}}\right)\right)$，而${\mathbf{x}}_{\mathbf{i}}$ 的后验概率可以计算为 $p_{\theta }\left({\mathbf{x}}_{\mathbf{i}}\mid {\mathbf{z}}_{\mathbf{t}-\mathrm{T}:\mathbf{i}}\right)\sim \mathcal{N}\left({\mu }_{{\mathbf{x}}_i},{\sigma }_{{\mathbf{x}}_i}^2\mathrm{I}\right)$。第二项和第三项之和是正则的 （即 Kullback-Leibler loss，KL 损失）。第二条 $\log \left(p_{\theta }\left({\mathbf{z}}_{\mathbf{t}-\mathrm{T}:\mathbf{t}}\right)\right)={\sum }_{i=t-T}^t\log \left(p_{\theta }\left({\mathbf{z}}_{\mathbf{i}}\mid {\mathbf{z}}_{\mathbf{i}-1}\right)\right)$，其中 ${\mathbf{z}}_{\mathbf{i}}$ 可以通过线性高斯SSM[8] 用标准多元正态分布初始化得到。 第三项是在 $qnet$ 中逼近 $z_i$ 在 $z$ 空间中的真实后验分布：$-\log \left(q_{\varphi }\left({\mathbf{z}}_{\mathbf{t}-\mathrm{T}:\mathbf{t}}\mid {\mathbf{x}}_{\mathbf{t}-\mathrm{T}:\mathrm{t}}\right)\right)=-{\sum }_{i=t-T}^t\log \left(q_{\varphi }\left({\mathbf{z}}_{\mathbf{i}}\mid {\mathbf{z}}_{\mathbf{i}-1},{\mathbf{x}}_{\mathbf{t}-\mathrm{T}:\mathbf{i}}\right)\right)\cdot {\mathbf{z}}_{\mathbf{i}}$ （即 ${\mathbf{z}}_{\mathbf{i}}^{\mathbf{K}}$ 通过 planar NF 进行转换) ${\mathbf{z}}_{\mathbf{i}}^{\mathbf{K}}=f^K\left(f^{K-1}\left(\dots f^1\left({\mathbf{z}}_{\mathbf{i}}^0\right)\right)\right)$ ，其中 ${\mathrm{z}}_{\mathrm{i}}^0={\mu }_{{\mathrm{z}}_{\mathrm{i}}}+{\xi }_{\mathrm{i}}{\sigma }_{{\mathrm{z}}_{\mathrm{i}}}$，${\xi }_i\sim \mathcal{N}(0,\mathrm{I})$ ， $f^k$ 的计算已经在 3.3 节说明。

19.3.3 在线检测

现在，我们可以使用训练的 OmniAnomaly 模型来确定在一个时间步长（例如 $t$ 时刻，记作 $x_t$）上的观测是否异常。注意OmniAnomery的输入是长度为 $T+1$ 的序列数据。因此，我们将序列 $x_{t-T:t}$，即 $x_t$ 和在它之前的连续观测作为输入来重建 $x_t$。正如文献 [24] 所建议的，这种重构可以用条件概率来进行评估 $\log \left(p_{\theta }\left({\mathbf{x}}_{\mathbf{t}}\mid {\mathbf{z}}_{\mathbf{t}-\mathbf{T}:\mathbf{t}}\right)\right)$ 。 这个重建概率作为我们模型中的异常分值。$x_t$ 的异常分值用 $S_t$表示，所以 $S_t=\log (P_{\theta }(x_t|z_{t-T:t}))$。高分意味着可以很好地重构输入数据 $x_t$。 如果一个观测遵循时间序列的正常模式，就可以以高置信度重构它。 另一方面，分数越小，观测结果越不可能被重构，因此异常的可能性越大。 即，如果 $S_t$ 低于异常阈值，则 $x_t$ 标记为异常； 否则 $x_t$ 是正常的。 接下来，我们描述了如何离线自动确定异常阈值。

19.3.4 选择异常阈值

如图2所示， 在离线训练过程中，我们利用一个多变量的时间序列，为每一个观测量计算一个异常分数。 然后所有异常得分形成一个单变量时间序列 $\{S_1,S_2,...,S_{N^{{}^{\prime }}}\}$。 接下来，我们遵循极值理论(Extreme Value Theory，EVT) 的原理离线设置异常阈值 $t{h}_F$ [22]。

EVT 是一种以寻找极值规律为目标的统计理论，而极值通常位于概率分布的尾部。 EVT 的优点是在求极值时不对数据分布作任何假设。 过峰值阈值 (Peak-Over-Threshold，POT) [22] 是 EVT 中的第二个定理。 POT 的基本思想是用带参数的广义帕累托分布 (Pareto distribution， GPD) 拟合概率分布的尾部。 我们采用 POT 来学习异常分数的阈值。 与传统的 POT 应用程序不同，这些应用程序侧重于“分布高端的值”，我们分析中的异常位于分布的低端。 因此，我们对 GPD 函数进行如下调整：

$$\bar{F}(s)=P(th-S>s\mid S<th)\sim {\left(1+\frac{\gamma s}{\beta }\right)}^{-\frac{1}{\gamma }}\text{\hspace{1em}(6)}$$

其中 $th$ 为异常得分的初始阈值，$\gamma$ 和 $\beta$ 为 GPD 的形状和尺度参数，$S$ 为 $\{S_1,S_2,...,S_{N^{{}^{\prime }}}\}$ 中的任意值。低于阈值 $th$ 的部分被表示为 $th-S$ ，并且根据经验将其设置为低分位数。与[22]类似，我们用极大似然估计(MLE)估计参数 $\hat{\gamma }$ 和 $\hat{\beta }$ 的值。 最终阈值 $t{h}_F$ 如下计算：

$$t{h}_F\simeq th-\frac{\hat{\beta }}{\hat{\gamma }}\left({\left(\frac{q{N}^{\prime }}{N_{th}^{\prime }}\right)}^{-\hat{\gamma }}-1\right)\text{\hspace{1em}(7)}$$

其中 $q$ 是观察到的期望概率 $S<th$，$N^{{}^{\prime }}$ 是观测数据的数量，$N_{th}^{{}^{\prime }}$ 是 $S_i$ 的数量，$S_i<th$。对于POT方法，只有两个参数（低分位数和 $q$）需要调优。 这两个参数是全模型的，可以根据经验设置：低分位数（例如，小于7%）和 $q$（例如，$10^{-4}$ ) [22]，见附录 B。

19.3.5 异常解释

正如第1节所述，我们的异常解释解决方案的目标是用按重建概率排序的前几个单变量时间序列来注释检测到的实体异常。 因此，我们必须求出 $x_t^i$ ( $x_t$ 的第 $i$ 个维度) 的重构概率。然而， 在 OmniAnomaly 中，计算了 $M$ 维 $x_t$ 的重构概率。 幸运的是，正如 4,2 章节所述，$p_{\theta }\left({\mathrm{x}}_{\mathrm{t}}\mid {\mathrm{z}}_{\mathrm{t}-\mathrm{T}:\mathrm{t}}\right)\sim \mathcal{N}\left({\mu }_{{\mathrm{x}}_{\mathbf{t}}},{\sigma }_{{\mathrm{x}}_t}^2\mathrm{I}\right)$ ，因此，$p_{\theta }\left({\mathbf{x}}_{\mathbf{t}}\mid {\mathbf{z}}_{\mathbf{t}-\mathrm{T}:\mathbf{t}}\right)={\prod }_{i=1}^M{p}_{\theta }\left(x_t^i\mid {\mathbf{z}}_{\mathbf{t}-\mathrm{T}:\mathbf{t}}\right)$。因此，$x_t$ 的条件概率可分解为：

$$\log \left(p_{\theta }\left({\mathbf{x}}_{\mathbf{t}}\mid {\mathbf{z}}_{\mathrm{t}-\mathrm{T}:\mathrm{t}}\right)\right)=\sum _{i=1}^M\log \left(p_{\theta }\left(x_t^i\mid {\mathbf{z}}_{\mathrm{t}-\mathrm{T}:\mathrm{t}}\right)\right)\text{\hspace{1em}(8)}$$

$S_t={\sum }_{i=1}^M{S}_t^i$ ，其中 $S_t^i=\log (p_{\theta }\left(x_t^i\mid {\mathbf{z}}_{\mathbf{t}-\mathrm{T}:\mathrm{t}}\right)$ ，而 $S_t^i$ 是 $x_t^i$ 的异常值。注意，$S_t^i$ 受益于多元时间序列 $x_{t-t:t-1}$ 中的丰富信息，因此它的解释能力高于仅利用 $x_{t-T:t-1}^i$ 获得的异常得分（如单变量时间序列中的异常得分）。

对于一个检测到的异常 $x_t$ ，我们通过估计 $x_t$ 各维的贡献（即重构概率）来解释它。我们将 $S_t^i$ ($1\le i\le M$) 按升序排序，形成列表 $A{S}_t$。对 $x_t^i$ ，$A{S}_t$ 排名越高，$S_t^i$ 越小，$x_t^i$ 对 $x_t$ 的贡献越大。 将有序列表作为异常解释提供给操作员，希望前几个维度能为操作员理解和排除检测到的实体异常提供足够的线索。

注意因式分解公式8 与 $p_{\theta }\left({\mathbf{x}}_{\mathbf{t}}\mid {\mathbf{z}}_{\mathbf{t}-\mathrm{T}:\mathbf{t}}\right)\sim \mathcal{N}\left({\mu }_{{\mathrm{x}}_t},{\sigma }_{{\mathrm{x}}_t}^2\mathrm{I}\right)$ 一样。因此，我们提出的异常解释方法也适用于其他多元时间序列异常检测算法，如[16]。

19.4 实验部分

19.4.1 数据集

实验基于三大数据集下进行：

• SMD (Server Machine Dataset)
• SMAP (Soil Moisture Active Passive satellite)
• MSL (Mars Science Laboratory rover).

数据集来源可以参考论文源码 https://github.com/NetManAIOps/OmniAnomaly，概括一下大致如下：

• 论文源码中包含的是 SMD 数据，具体的地址为 https://github.com/NetManAIOps/OmniAnomaly/tree/master/ServerMachineDataset
• SMAP 和 MSL 数据下载链接为 ：https://s3-us-west-2.amazonaws.com/telemanom/data.zip 以及对应的 标签https://raw.githubusercontent.com/khundman/telemanom/master/labeled_anomalies.csv 。

19.4.2 实验环境搭建

为了方便，我们使用 docker 搭建实验环境，希望对 docker 不了解的小伙伴稍微花费点点时间了解一下即可，整个过程相对以前而言简单很多，具体内容请参考 https://blog.csdn.net/smileyan9/article/details/127592804

OmniAnomaly运行过程视频录制

19.4.3 对比实验

根据论文实验部分，可以看到论文的实验结果大致如下：

其中的 Donut 与 LSTM-VAE 在本系列博客中已经介绍过，可以自行复现。


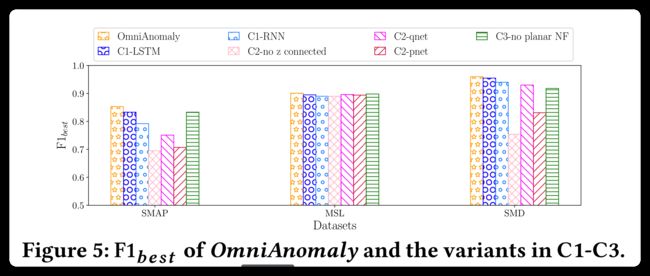
实验结果的分析等等内容这里不做介绍。

19.5 总结

这里没有提供对论文的全文翻译内容，但最核心部分的内容都已经翻译如文中所示。

算法的核心部件依然是 VAE，但是添加了一些自己的内容，并且使得 VAE 这种基于单指标的算法应用在多特征中。

论文的图片绘制或多或少有些不够漂亮，尤其是图3，实在忍不住想吐槽两句（见谅见谅）。

论文的源码的介绍，以及数据集的介绍都非常详细，总体来说还是很不错的，值得相关领域小伙伴们引用并作为对比实验的。

最后补充一下如非必要，均不用太在意最终输出结果是什么，结果怎么样。最主要的应该是了解论文思路，不停地查资料，来扩充自己对这方面的了解。一般情况下，只有在试图改进这个算法以及需要拿这个算法做对比实验的时候，才需要耐心跑完，分析结果。

感谢各位小伙伴的一路支持 ~ 非常感谢 ~

Smileyan
2022.10.30 23:29