漫步微积分二十七——曲线下的面积 定积分 黎曼

我们继续讨论我们要解决的问题。 y=f(x) 是定义在闭区间 a≤x≤b 上的非负函数，如图1所示。我们如何计算阴影部分(即图像下方， x 轴上方以及垂直直线x=a,x=b共同围成的部分)面积呢？

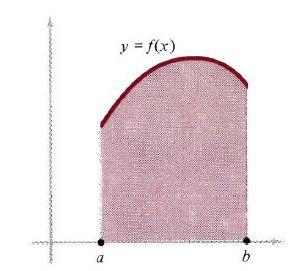
图1}

像这里提到的闭区间会经常出现在我们的讨论中，所以我们用更简短的符号 [a,b] 表示。此外，我们研究的大多数函数都是连续的。这意味着：从直观的角度来看，图像由一片组成，没有隙缝或洞；更确切地说， [a,b] 上的每个点 c ，一定满足

limx→cf(x)=f(c)

这种函数具有几个基本属性：它是有界的，也就是说存在常数 K 使得区间[a,b]上的所有 x 都满足f(x)≤K；存在最大和最小值，也就是说图像有最高和最低点。

回到图1，符合在 [a,b] 上函数 y=f(x) 连续。我们如何找出阴影区域的面积呢？考虑区域的性质，即只要上边是曲线，那么通过狭小的矩形可以逼近出近似值。

n 是一个正整数，区间[a,b]分割成相等的 n 个子区间。将每个子区间作为底，构建一个曲线下方最高的矩形。所有这些长方形面积的总和为用sn表示。和的面积近似等于图形的面积， n 越大就越相似，或等价地，区间[a,b] 被分成更多更小的子区间。最后，通过求出 sn 的极限值得出图像面积的准确值：

area of region=limn→∞sn(1)

这个过程的效果如图2，矩形越细，它的数目就越多。

现在我们引入一些合适的符号更准确的描述这个想法。

图2

依然是， n 是一个正整数，区间[a,b]分割成相等的 n 个子区间，在区间内插入n−1个间隔点 x1,x2,…,xn−1 。如果用 a 表示x0， b 表示xn，那么这些自区间的端点是

a=x0<x1<x2<⋯<xn−1<xn=b(2)

子区间为

[x0,x1],[x2,x3],…,[xn−1,xn](3)

如图3所示。我们用 Δxk 表示第 k 个子区间，那么

Δxk=xk−xk−1(4)

图3

因为子区间长度相等，很明显 Δxk=(b−a)/n 。让 mk 表示 f(x) 在第 k 个区间[xk−1,xk]上的最小值。子区间内的对应点假定为 x¯k ：

f(x¯k)=mk,xk−1≤x¯k≤xk

对于图3的情况， x¯k 很明显看出是当曲线上升时是子区间的左端点，当下降时是右端点。因为每个内嵌矩形的面积都是底乘高，所以所有矩阵面积的和 sn 为

sn=f(x¯1)Δx1+f(x¯2)Δx2+⋯+f(x¯k)Δxk+⋯+f(x¯n)Δxn

用sigma符号来简化求和公式得

sn=∑k=1nf(x¯k)Δxk(5)

(1)就变成了

area of region=limn→∞∑k=1nf(x¯k)Δxk(6)

这个公式正确性自然不言而喻，但从某些方面来说它不方便而且限制也比较多。我们扩大一下它的范围并深化其意义。

注解1：子区间(3)的长度没有必要一定相等。事实上，如果去掉了这个限制，基本理论将大大简化。因此，我们允许子区间(3)长度不相等，以便增量(4)彼此间可以不同。在公式(6)中，就没必要让 n 趋于无穷大；我们必须要求最长区间的长度趋于零。因为后者的条件包括了前者，因此(6)可以换为

area of region=limmax Δxk→∞∑k=1nf(x¯k)Δxk(7)

其中 Δxk 表示最长子区间的长度。

注解2：(5)的总和称为下部和，因为它使用的内接矩形和从区域的下方逼近面积。我们也可以从上面逼近面积。粗略地说，我们依然使用之前的子区间作为底，但我们构建的矩形是曲线上面最低的。

为了用符号说明，我们用 Mk 表示第 k 个区间[xk−1,xk]上 f(x) 的最大值。这个最大值假定在区间内点 x¯¯k 处取得：

f(x¯¯k)=Mk,xk−1≤x¯¯k≤xk

矩形面积之和为

Sn=∑k=1nf(x¯¯k)Δxk(8)

这称作上部和，因此它从上面逼近区域面积，如图4所示。几何直觉告诉我们，当取上部和的极限时，我们同样能得到较好的区域面积，所以我们有

area of region=limmax Δxk→∞∑k=1nf(x¯¯k)Δxk(9)

然而，除了直觉(有时会产生误导)外，它可以用纯数学定理来证明，对任何连续函数，(7)(9)的极限都存在且有相同的函数值。

图4

更进一步，如果 x∗k 取第 k 个区间[xk−1,xk]上 f(x) 的任意一点，那么我们有

sn≤∑k=1nf(x∗k)Δxk≤Sn

那么(7)(9)描述的定理就能换成如下的形式

area of region=limmax Δxk→∞∑k=1nf(x∗k)Δxk(10)

其中对 x∗k 只存在一个约束 xk−1≤x∗k≤xk

注解3：(10)或(7)或(9)的极限用标准的莱布尼兹符号表示是

∫baf(x)dx(11)

如果要写出(11)的定义，

∫baf(x)dx=limmax Δxk→∞∑k=1nf(x∗k)Δxk(12)

左侧符号的每一部分都在提醒我们相应的右侧逼近和的部分。积分符号 ∫ 是拉长的字母 S ，就像“sum”，因为定积分和和的相似性所以选择了它；(12)的极限端似乎用∫替换了 ∑ 。此外，常用的增量符号 Δ 用字母 d 取代，这提醒我们这是个极限运算，就像莱布尼茨符号dy/dx。 因此，对于(12)的极限端

∑k=1nf(x∗k)Δxkbecomes∫babecomesf(x)becomesdx

积分符号上的数字 a,b 叫做积分的上下限。定积分中，积分限总是存在的，这有助于区分不定积分

∫f(x)dx

(11)中的函数 f(x) 称为被积函数，变量 x 是积分变量。作为定积分直观特征的dx，我们后面后详细介绍。

注解4：目前为止，我们采纳朴素但合理的态度，即图像区域下方的面积明显存在，而且我们需要做的是设计方法来计算它。然而，下面的示例表明，情况比我们想象的要复杂。

考虑区间 [0,1] 上的函数 f(x)

f(x)={01如果x是有理数如果x是无理数

图像如图5所示，这个函数是不连续的，因为至少存在一个无理数介于每对有理数之间并且至少存在一个有理数介于每对无理数之间。根据此图，区域的面积是什么呢？很容易看到每个下部和是0而上部和是1，所以由(7)计算面积的面积是0和由(9)计算的面积是1。此外，(12)右边的极限不存在。像这种情况，面积的概念还有意义吗？

这个怪异的例子给出了以下间接但更有逻辑的面积问题的求法。如果我们给定一个有界的非负函数 f(x) ，但在区间 [a,b] 上不一定连续，现在我们开始检查(12)右边的极限。如果极限存在，那么我们将它定义为区域下面的面积，并且我们说函数 f(x) 在 [a,b] 上是可积的。如果极限不存在，那么将面积的没有意义。我们在实践中遇到几乎所有函数都是连续的，注解2所述的定理保证每个连续函数是可积的，所以这些逻辑的细点在我们大多数的工作中意义不大。然而，这些问题从微积分基本理论的角度来讲是有趣和重要的，学生应该知道他们，即便我们不去强调他们。

图5

这里定义的定积分通常称为黎曼积分，他是十九世纪德国数学家，因为他第一个给出了不连续函数积分的详细讨论，所以为了纪念他就称为黎曼积分。此外，(12)右侧的和通常称为黎曼和。