spatialreg | 空间滞后模型、空间误差模型和空间杜宾模型简单形式的R语言实现...
旧文重发,原文链接:https://mp.weixin.qq.com/s/pHRS9BfkCMe1uQOSkHmqAw
关于空间计量模型,小编是通过阅读勒沙杰(James LeSage)和佩斯(R.Kelley Pace)合著的《空间计量经济学导论》(Introduction of Spatial Econometrics)入门的,但是当时着重的是理解这些模型,并没有用代码去实现。
作者也提供了书中模型的Matlab代码,可以在网站http://www.spatial-econometrics.com/(Econometrics Toolbox: by James P. LeSage)上查看。另外,作者之一的佩斯还有一个网站http://www.spatial-statistics.com/(Spatial Statistics Software and Articles),上面有一些空间统计领域的Matlab工具箱和论文。
由于小编目前也在学习阶段,因此本篇只会使用R语言去实现这些模型的一些比较简单的形式,使用的工具包是spatialreg,后续可能会分享一些更复杂的内容。
1 模型形式
1.1 空间滞后模型
自回归模型(Autoregressive Model,AR)在时间序列分析中很易理解,即因变量与它的时间滞后值(Lag)存在相关性,这也意味着自回归模型放弃了因变量独立性的假设。
在空间计量模型中,空间滞后值被认为是邻近空间单元的属性(加权)值,因此下面是一个形式比较简单的空间自回归模型(最简单的形式应该是不包含自变量),也就是空间滞后模型(Spatial Lagged Model,SLM):
空间自回归模型一般就是指空间滞后模型,但它也有一个更广义的概念,即所有包含因变量的空间滞后项的模型;
模型估计时会首先对参数进行估计,再使用广义最小二乘法估计和其他参数。
1.2 空间误差模型
空间误差模型(Spatial Error Model,SEM)可以分解成如下两步:
上述两式合并得,
402 Payment Required
第一个式子并非线性模型,因为不需要服从正态分布;
模型估计时会首先对参数进行估计,再使用广义最小二乘法估计和其他参数。
1.3 空间杜宾模型
空间杜宾模型(Spatial Durbin Model,SDM)假定因变量取值除受本地自变量的影响外,还会受到邻近地区的自变量影响,即在模型中加入自变量的空间滞后值:
402 Payment Required
1.4 复合模型
上述三个模型各自有针对性的假设,但这些假设相互之间并不排斥,可以在同一个模型中存在。
1.4.1 空间自相关模型
该模型综合了空间滞后模型和空间误差模型,称作空间自相关模型(Spatial Autocorrelation Model,SAC);
当或其中一个为0时,SAC就退化成了SEM或SLM。
1.4.2 空间杜宾(滞后)模型
402 Payment Required
该模型综合了空间滞后模型和空间杜宾模型,但习惯上仍称作是空间杜宾模型。
1.4.3 空间杜宾误差模型
该模型综合了空间误差模型和空间杜宾模型,称作空间杜宾误差模型(Spatial Durbin Error Model,SDEM)。
1.4.4 空间自相关杜宾模型
该模型是最一般的形式,同时综合了三种基本模型,也可以认为是综合了空间自相关模型和空间杜宾模型。
2 R语言代码
2.1 函数概述
上述7个模型形式可以通过spatialreg工具包中的3个函数来实现:
lagsarlm():空间滞后模型、空间杜宾(滞后)模型errorsarlm():空间误差模型、空间杜宾误差模型sacsarlm():空间自相关模型、空间自相关杜宾模型
2.2 线性模型
示例数据如下:
library(sf)
library(tidyverse)
usa <- albersusa::counties_sf(proj = "laea") %>%
mutate(fips = as.character(fips)) %>%
left_join(socviz::county_data, by = c("fips" = "id"))因变量取收入,自变量取黑人比例。在运行空间计量模型前,先使用线性模型进行建模:
data <- st_drop_geometry(usa)
model <- lm(hh_income ~ black, data = data)
summary(model)
## Call:
## lm(formula = hh_income ~ black, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -27680 -7341 -2171 4653 76006
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 47765.53 244.55 195.32 <2e-16 ***
## black -199.18 14.29 -13.94 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 11570 on 3141 degrees of freedom
## Multiple R-squared: 0.05825, Adjusted R-squared: 0.05795
## F-statistic: 194.3 on 1 and 3141 DF, p-value: < 2.2e-162.3 莫兰指数
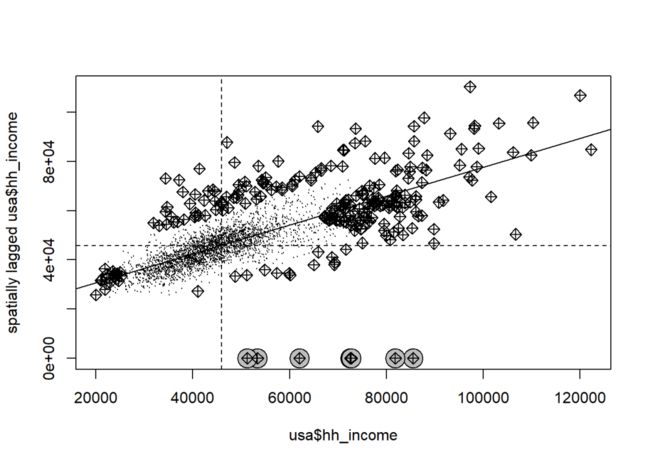
使用莫兰指数检验因变量的空间自相关性:
library(spdep)
nb <- poly2nb(usa)
listW <- nb2listw(nb, zero.policy = T)
jpeg("1.jpeg", width = 8, height = 6, res = 600, units = "in")
moran.plot(usa$hh_income, listW,
zero.policy = T,
labels = F,
pch = 20, cex = 0.1)
dev.off()
部分县没有邻接单元,设置
zero.policy = T可以允许空间权重矩阵(实际空间数据结构是list)存在空元素。
2.4 空间计量模型
以lagsarlm()函数为例,它的完整语法结构如下:
lagsarlm(formula, data = list(),
listw, na.action,
Durbin, type,
method="eigen", quiet=NULL,
zero.policy=NULL, interval=NULL,
tol.solve=.Machine$double.eps,
trs=NULL, control=list())本篇仅涉及以下几个参数,其余参数使用...代替:
lagsarlm(formula, data = list(),
listw, Durbin,
zero.policy = NULL,
...,)
formula:与对应的线性模型的表达式一致;
data:变量所在的数据框;
listw:空间权重矩阵;
Durbin:是否在模型中加入自变量的空间滞后值;
zero.policy:针对权重矩阵存在空元素的应对方案,TRUE表示对应的空间滞后的权重为0。
2.4.1 空间滞后模型
library(spatialreg)
sl_model <- lagsarlm(hh_income ~ black, data = data,
listw = listW, zero.policy = T)
summary(sl_model)
## Call:lagsarlm(formula = hh_income ~ black, data = data, listw = listW,
## zero.policy = T)
##
## Residuals:
## Min 1Q Median 3Q Max
## -26914.4 -4772.3 -1298.9 2996.4 72040.0
##
## Type: lag
## Regions with no neighbours included:
## 2788 2836 2995 3135 3140 3141 3143
## Coefficients: (numerical Hessian approximate standard errors)
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 14401.438 628.923 22.899 < 2.2e-16
## black -121.955 10.236 -11.915 < 2.2e-16
##
## Rho: 0.71234, LR test value: 1783.5, p-value: < 2.22e-16
## Approximate (numerical Hessian) standard error: 0.012906
## z-value: 55.195, p-value: < 2.22e-16
## Wald statistic: 3046.5, p-value: < 2.22e-16
##
## Log likelihood: -32973.68 for lag model
## ML residual variance (sigma squared): 67335000, (sigma: 8205.8)
## Number of observations: 3143
## Number of parameters estimated: 4
## AIC: 65955, (AIC for lm: 67737)2.4.2 空间误差模型
library(spatialreg)
se_model <- errorsarlm(hh_income ~ black, data = data,
listw = listW, zero.policy = T)
summary(se_model)
## Call:errorsarlm(formula = hh_income ~ black, data = data, listw = listW,
## zero.policy = T)
##
## Residuals:
## Min 1Q Median 3Q Max
## -30053.7 -4590.2 -1184.3 2843.3 56012.9
##
## Type: error
## Regions with no neighbours included:
## 2788 2836 2995 3135 3140 3141 3143
## Coefficients: (asymptotic standard errors)
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 50696.822 725.463 69.882 < 2.2e-16
## black -400.074 18.035 -22.183 < 2.2e-16
##
## Lambda: 0.82333, LR test value: 2384.3, p-value: < 2.22e-16
## Approximate (numerical Hessian) standard error: 0.011128
## z-value: 73.99, p-value: < 2.22e-16
## Wald statistic: 5474.5, p-value: < 2.22e-16
##
## Log likelihood: -32673.29 for error model
## ML residual variance (sigma squared): 52510000, (sigma: 7246.4)
## Number of observations: 3143
## Number of parameters estimated: 4
## AIC: 65355, (AIC for lm: 67737)2.4.3 空间杜宾误差模型
library(spatialreg)
sd_model <- errorsarlm(hh_income ~ black, data = data,
listw = listW, zero.policy = T,
Durbin = T)
summary(sd_model)
## Call:errorsarlm(formula = hh_income ~ black, data = data, listw = listW,
## Durbin = T, zero.policy = T)
##
## Residuals:
## Min 1Q Median 3Q Max
## -29657.6 -4639.4 -1123.4 2817.7 56324.1
##
## Type: error
## Regions with no neighbours included:
## 2788 2836 2995 3135 3140 3141 3143
## Coefficients: (asymptotic standard errors)
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 48577.976 753.720 64.4509 < 2.2e-16
## black -392.654 17.888 -21.9512 < 2.2e-16
## lag.black 223.080 36.404 6.1278 8.909e-10
##
## Lambda: 0.81169, LR test value: 2384.6, p-value: < 2.22e-16
## Approximate (numerical Hessian) standard error: 0.011396
## z-value: 71.228, p-value: < 2.22e-16
## Wald statistic: 5073.5, p-value: < 2.22e-16
##
## Log likelihood: -32655.17 for error model
## ML residual variance (sigma squared): 52280000, (sigma: 7230.5)
## Number of observations: 3143
## Number of parameters estimated: 5
## AIC: 65320, (AIC for lm: 67703)