(01)ORB-SLAM2源码无死角解析-(22) 特征点三角化、深度计算、三维点筛选
讲解关于slam一系列文章汇总链接:史上最全slam从零开始,针对于本栏目讲解的(01)ORB-SLAM2源码无死角解析链接如下(本文内容来自计算机视觉life ORB-SLAM2 课程课件):
(01)ORB-SLAM2源码无死角解析-(00)目录_最新无死角讲解:https://blog.csdn.net/weixin_43013761/article/details/123092196
文末正下方中心提供了本人 联系方式, 点击本人照片即可显示 W X → 官方认证 {\color{blue}{文末正下方中心}提供了本人 \color{red} 联系方式,\color{blue}点击本人照片即可显示WX→官方认证} 文末正下方中心提供了本人联系方式,点击本人照片即可显示WX→官方认证
一、前言
通过前面的博客,我们已经知道如何从 单应性矩阵Homography,或者 基本矩阵Fundamental 中恢复 R t \mathbf R\mathbf t Rt,但是这里存在一个比较尴尬的问题,其结果都存在多组解,也就是多组 R t \mathbf R\mathbf t Rt,比如从 Homography 中恢复 R t \mathbf R\mathbf t Rt 存在8组解,从 Fundamental 中恢复 存在4组解。那么我们如何去判断那组解是最优的呢?
在 Initializer.cc 文件中,之前介绍的两个函数: ReconstructH() 与 ReconstructF(), 都调用了一个比较重要的函数→CheckRT(),该函数主要是对 R t \mathbf R\mathbf t Rt 进行评估,得出其可靠性与稳定性。该代码中主要涉及的东西包含:特征点三角化、重投影误差。
三角化在不同位置观测同一个三维点 X = ( X , Y , Z ) \mathbf X=(X,Y,Z) X=(X,Y,Z),其在二维的投影是不一样的,设两个位置的二维投影(归一化后特征点坐标)为 x 1 \mathbf x_1 x1, x 2 \mathbf x_2 x2,视角关系如下:
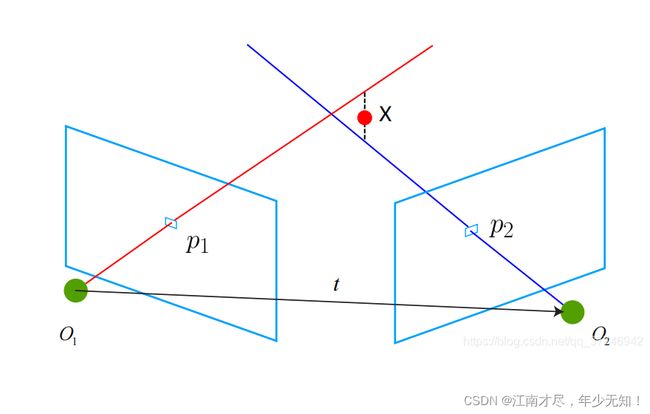
红线与蓝线因为噪音的影响,是没有办法相交的。主要的目的,就是利用上图的三角信息,恢复出三维点的深度信息 Z Z Z。
二、基础理论
假设三维点 X = ( X , Y , Z ) T \mathbf X=(X,Y,Z)^T X=(X,Y,Z)T, 投影之后归一化特征点坐标 x 1 , x 2 \mathbf x_1,\mathbf x_2 x1,x2,分别对应投影矩阵 P 1 P_1 P1, P 2 P_2 P2,那么他们之间的转换关系如下, 如果已知 R t \mathbf R\mathbf t Rt 满足如下关系:
s 1 x 1 = s 2 R x 2 + t (01) \tag{01} \color{blue} s_1 \mathbf x_1=s_2 \mathbf R \mathbf x_2+\mathbf t s1x1=s2Rx2+t(01)现在需要求解两个特征点的深度 s 1 , s 2 s_1,s_2 s1,s2, 当然这两个深度是可以分开求的,比如说 s 2 s_2 s2,如果我们要算 s 2 s_2 s2,式子两侧都左乘一个 x 1 ∧ \mathbf x_1^{\wedge} x1∧(列向量的反对称矩阵,如果不是很理解得朋友可以百度一下向量叉乘)。
s 1 x 1 ∧ x 1 = 0 = s 2 x 1 ∧ R x 2 + x 1 ∧ t (02) \tag{02} \color{blue} s_{1} \mathbf {x}_{1}^{\wedge} \mathbf {x}_{1}=0=s_{2} \mathbf {x}_{1}^{\wedge} \mathbf {R} \mathbf {x}_{2}+\mathbf{x}_{1}^{\wedge} \mathbf t s1x1∧x1=0=s2x1∧Rx2+x1∧t(02)该式左侧为0,右侧可看成 s 2 s_2 s2的一个方程。可以直接求解 s 2 s_2 s2, 有了 s 2 s_2 s2, s 1 s_1 s1 也非常容易求出,这样就能获得两帧下点的帧深度。也就确定了它们的空间坐标,当然,由于噪声的存在,我们估得 R t \mathbf R\mathbf t Rt,不一定精确使得(01)式有解,所以常见得做法是最小二乘,而不是零解。
另外还存在一个问题,从式(02)我们可以看出,当 t \mathbf t t 为0时,也就是图一中的红线与蓝线重合,无法产生三角形,处于红线(蓝线)上的任意一点,都满足其投影 ,故存在无穷多解。也就是 X \mathbf X X 不唯一。同时如果平移距离比较小,则改变的一个很小的角度会导致深度大幅变化,如下图:
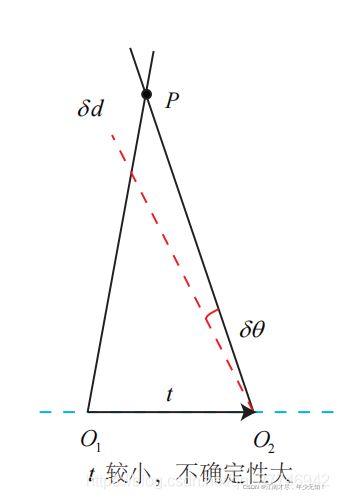
上图是相机 O 2 O_2 O2 向左旋转,那么我们现象一种极端情况,就是 t \mathbf t t 无穷小,那么 O 2 O_2 O2 向右旋转一点点,他们的交点到了无穷远处,也就是深度无穷大。总的来说, 就是 t \mathbf t t 比较小的时候, R \mathbf R R 的一点点误差,会导致深度 Z Z Z 会偏差很大。 但是呢,平移过大则会导致特征匹配失败,这就是三角化的矛盾。
因此,为了增加三角化的精度,可以提高特征点的提取精度,也就是提高图像分辨率,但是会加大计算量;或者增大平移量,但是容易导致图像变化过大,进而导致匹配难度的增加,导致匹配失败。下面再来看看根据一对特征点求解 X = ( X , Y , Z ) T \mathbf X=(X,Y,Z)^T X=(X,Y,Z)T 的矩阵推导。
三、公式推导
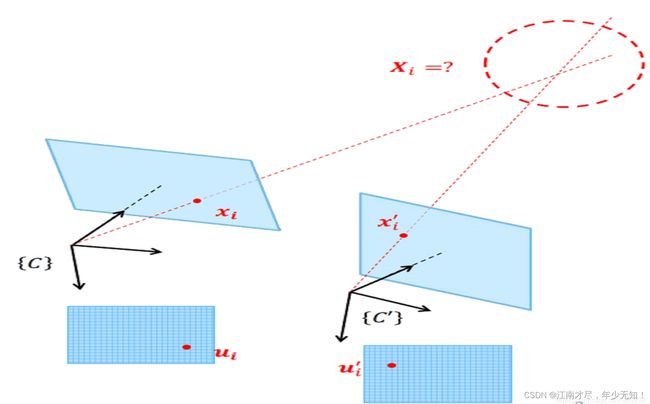
如上图所示, X \mathbf X X 为三维空间点在世界坐标系下的齐次坐标, T \mathbf T T 为世界坐标到相机坐标的变换矩阵,以及 x \mathbf x x 为归一化平面坐标, λ \lambda λ 为深度值,如下所示:
X = [ X Y Z 1 ] T = [ r 1 r 2 r 3 ] = [ R ∣ t ] x = [ u v 1 ] (03) \tag{03} \color{blue} \mathbf X=\left[\begin{array}{l} X \\ Y \\ Z \\ 1 \end{array}\right]~~~~~~\mathbf T=\left[\begin{array}{l} r_1 \\ r_2 \\ r_3 \\ \end{array}\right]=[\mathbf R|\mathbf t]~~~~~~\mathbf{x}=\left[\begin{array}{l} u \\ v \\ 1 \end{array}\right] X=⎣ ⎡XYZ1⎦ ⎤ T=⎣ ⎡r1r2r3⎦ ⎤=[R∣t] x=⎣ ⎡uv1⎦ ⎤(03) 这里需要注意一个点 \color{red}{这里需要注意一个点} 这里需要注意一个点 ,对于其上 x \mathbf{x} x 的坐标1,是有特殊含义的,这里默认相机圆心到成像平面的距离(焦距)为1,也就是进行单位化,如果后续需要计算真实3D坐标,需要乘以焦距。根据相机成像原理,则存在:
λ x = T X λ x × T X = 0 x ∧ T X = 0 (04) \tag{04} \color{blue} \begin{array}{c} \lambda \mathbf{x}=\mathbf T \mathbf X \\ \lambda \mathbf{x} \times \mathbf T \mathbf X=\mathbf 0 \\ \mathbf x^{\wedge} \mathbf T \mathbf X=\mathbf 0 \end{array} λx=TXλx×TX=0x∧TX=0(04)然后我们向量叉乘的公式进行展开: x ∧ T X = [ 0 − 1 v 1 0 − u − v u 0 ] [ r 1 r 2 r 3 ] X = 0 (05) \tag{05} \color{blue} \mathbf{x}^{\wedge} \mathbf T \mathbf X=\left[\begin{array}{ccc} 0 & -1 & v \\ 1 & 0 & -u \\ -v & u & 0 \end{array}\right]\left[\begin{array}{l} {r}_{1} \\ {r}_{2} \\ {r}_{3} \end{array}\right] \mathbf X=\mathbf 0 x∧TX=⎣ ⎡01−v−10uv−u0⎦ ⎤⎣ ⎡r1r2r3⎦ ⎤X=0(05)进一步进行简化 x ∧ T X = [ − r 2 + v r 3 r 1 − u r 3 − v r 1 + u r 2 ] X = 0 A = [ − r 2 + v r 3 r 1 − u r 3 − v r 1 + u r 2 ] (06) \tag{06} \color{blue} \mathbf{x}^{\wedge} \mathbf T \mathbf X =\left[\begin{array}{c} -{r}_{2}+v {r}_{3} \\ {r}_{1}-u {r}_{3} \\ -v {r}_{1}+u {r}_{2} \end{array}\right] \mathbf X=\mathbf 0~~~~~~~~\mathbf A= \left[\begin{array}{c} -{r}_{2}+v {r}_{3} \\ {r}_{1}-u {r}_{3} \\ -v {r}_{1}+u {r}_{2} \end{array}\right] x∧TX=⎣ ⎡−r2+vr3r1−ur3−vr1+ur2⎦ ⎤X=0 A=⎣ ⎡−r2+vr3r1−ur3−vr1+ur2⎦ ⎤(06)这个时候我认真观察一下,可以发现矩阵 A \mathbf A A 的第一行乘以 − u -u −u,第二行乘以 − v -v −v, 再相加,即可得到第三行,因此其是线性相关,保留前两行即可,那么可以的推理出: x ∧ T X = [ v r 3 − r 2 r 1 − u r 3 ] X = 0 (07) \tag{07} \color{blue} \mathbf{x}^{\wedge} \mathbf T \mathbf X =\left[\begin{array}{c} v {r}_{3} -{r}_{2}\\ \\ {r}_{1}-u {r}_{3} \\ \end{array}\right] \mathbf X=\mathbf 0 x∧TX=⎣ ⎡vr3−r2r1−ur3⎦ ⎤X=0(07)上面的推导是针对于一个特征点,如果是一对特征点(不同成像平面),可以写成如下公式(同一相机)
x ∧ T X = [ v 1 r 3 − r 2 r 1 − u 1 r 3 v 2 r 3 − r 2 r 1 − u 2 r 3 ] [ X Y Z 1 ] = A X = 0 (08) \tag{08} \color{blue} \mathbf{x}^{\wedge} \mathbf T \mathbf X =\left[\begin{array}{c} v_1 {r}_{3} -{r}_{2}\\ {r}_{1}-u_1 {r}_{3} \\ v_2 {r}_{3} -{r}_{2}\\ {r}_{1}-u_2 {r}_{3} \\ \end{array}\right] \left[\begin{array}{l} X \\ Y \\ Z \\ 1 \end{array}\right]= \mathbf A \mathbf X=\mathbf 0 x∧TX=⎣ ⎡v1r3−r2r1−u1r3v2r3−r2r1−u2r3⎦ ⎤⎣ ⎡XYZ1⎦ ⎤=AX=0(08)
直接对 A \mathbf A A 进行 SVD 奇异值分解,然后根据最小二乘法的推导,即可得到其最优解。最优解为,分解之后最小奇异值对应于右奇异矩阵的特征向量。也就矩阵 V \mathbf V V 的最后一列。即 V T \mathbf V^T VT 最后一行。
四、三维点筛选
根据上述的公式,已经知道如何根据特征点对进行三角化,那么三角化之后的结果是否正确?这个时候我们需要对三角化的结果进行验证。验证主要分为以下几个步骤:
步骤一 \color{blue}步骤一 步骤一: 根据前面的介绍,如果 t \mathbf t t 较小,则求解出来的 X \mathbf X X 坐标,可能存在无穷大的数值,则认为三角化失败。
步骤二 \color{blue}步骤二 步骤二: 判断视差,可以理解为图一红线与蓝线的夹角。如果视差太小,则认为认为三角化失败。
步骤三 \color{blue}步骤三 步骤三: 计算重投影误差,如果误差太大,则任务三角化失败(并且视察不能为负数,也就是三维点需要在相机前方)。
其上的步骤一与步骤二都比较好理解,这里我们重点讲解以下步骤三,其细化流程如下:
1.把第一个相机坐标系下的三维点 X 1 \mathbf X_1 X1,通过 R t \mathbf R\mathbf t Rt 矩阵转换成第二个相机坐标系下的三维点 X 2 \mathbf X_2 X2。
2.再根据计算出来的深度 Z Z Z,求解出该三维点第二个相机下的新图像坐标。
3.使用新图像坐标与特征点2作差,然后再作平方差计算,该结果,即认为是重投影误差。
五、代码注释
代码主调函数位于 Initializer.cc 文件中的 Initializer::CheckRT() 函数,其主要包含的部分为三角化函数Triangulate(),实现如下:
/** 给定投影矩阵P1,P2和图像上的匹配特征点点kp1,kp2,从而计算三维点坐标
* @brief
*
* @param[in] kp1 特征点, in reference frame
* @param[in] kp2 特征点, in current frame
* @param[in] P1 投影矩阵P1
* @param[in] P2 投影矩阵P2
* @param[in & out] x3D 计算的三维点
*/
void Initializer::Triangulate(
const cv::KeyPoint &kp1, //特征点, in reference frame
const cv::KeyPoint &kp2, //特征点, in current frame
const cv::Mat &P1, //投影矩阵P1
const cv::Mat &P2, //投影矩阵P2
cv::Mat &x3D) //三维点
{
// 原理
// Trianularization: 已知匹配特征点对{x x'} 和 各自相机矩阵{P P'}, 估计三维点 X
// x' = P'X x = PX
// 它们都属于 x = aPX模型
// |X|
// |x| |p1 p2 p3 p4 ||Y| |x| |--p0--||.|
// |y| = a |p5 p6 p7 p8 ||Z| ===>|y| = a|--p1--||X|
// |z| |p9 p10 p11 p12||1| |z| |--p2--||.|
// 采用DLT的方法:x叉乘PX = 0
// |yp2 - p1| |0|
// |p0 - xp2| X = |0|
// |xp1 - yp0| |0|
// 两个点:
// |yp2 - p1 | |0|
// |p0 - xp2 | X = |0| ===> AX = 0
// |y'p2' - p1' | |0|
// |p0' - x'p2'| |0|
// 变成程序中的形式:
// |xp2 - p0 | |0|
// |yp2 - p1 | X = |0| ===> AX = 0
// |x'p2'- p0'| |0|
// |y'p2'- p1'| |0|
// 然后就组成了一个四元一次正定方程组,SVD求解,右奇异矩阵的最后一行就是最终的解.
//这个就是上面注释中的矩阵A
cv::Mat A(4,4,CV_32F);
//构造参数矩阵A
A.row(0) = kp1.pt.x*P1.row(2)-P1.row(0);
A.row(1) = kp1.pt.y*P1.row(2)-P1.row(1);
A.row(2) = kp2.pt.x*P2.row(2)-P2.row(0);
A.row(3) = kp2.pt.y*P2.row(2)-P2.row(1);
//奇异值分解的结果
cv::Mat u,w,vt;
//对系数矩阵A进行奇异值分解
cv::SVD::compute(A,w,u,vt,cv::SVD::MODIFY_A| cv::SVD::FULL_UV);
//根据前面的结论,奇异值分解右矩阵的最后一行其实就是解,原理类似于前面的求最小二乘解,四个未知数四个方程正好正定
//别忘了我们更习惯用列向量来表示一个点的空间坐标
x3D = vt.row(3).t();
//为了符合其次坐标的形式,使最后一维为1
x3D = x3D.rowRange(0,3)/x3D.at<float>(3);
}
/**
* @brief 用位姿来对特征匹配点三角化,从中筛选中合格的三维点
*
* @param[in] R 旋转矩阵R
* @param[in] t 平移矩阵t
* @param[in] vKeys1 参考帧特征点
* @param[in] vKeys2 当前帧特征点
* @param[in] vMatches12 两帧特征点的匹配关系
* @param[in] vbMatchesInliers 特征点对内点标记
* @param[in] K 相机内参矩阵
* @param[in & out] vP3D 三角化测量之后的特征点的空间坐标
* @param[in] th2 重投影误差的阈值
* @param[in & out] vbGood 标记成功三角化点?
* @param[in & out] parallax 计算出来的比较大的视差角(注意不是最大,具体看后面代码)
* @return int
*/
int Initializer::CheckRT(const cv::Mat &R, const cv::Mat &t, const vector<cv::KeyPoint> &vKeys1, const vector<cv::KeyPoint> &vKeys2,
const vector<Match> &vMatches12, vector<bool> &vbMatchesInliers,
const cv::Mat &K, vector<cv::Point3f> &vP3D, float th2, vector<bool> &vbGood, float ¶llax)
{
// 对给出的特征点对及其R t , 通过三角化检查解的有效性,也称为 cheirality check
// Calibration parameters
//从相机内参数矩阵获取相机的校正参数
const float fx = K.at<float>(0,0);
const float fy = K.at<float>(1,1);
const float cx = K.at<float>(0,2);
const float cy = K.at<float>(1,2);
//特征点是否是good点的标记,这里的特征点指的是参考帧中的特征点
vbGood = vector<bool>(vKeys1.size(),false);
//重设存储空间坐标的点的大小
vP3D.resize(vKeys1.size());
//存储计算出来的每对特征点的视差
vector<float> vCosParallax;
vCosParallax.reserve(vKeys1.size());
// Camera 1 Projection Matrix K[I|0]
// Step 1:计算相机的投影矩阵
// 投影矩阵P是一个 3x4 的矩阵,可以将空间中的一个点投影到平面上,获得其平面坐标,这里均指的是齐次坐标。
// 对于第一个相机是 P1=K*[I|0]
// 以第一个相机的光心作为世界坐标系, 定义相机的投影矩阵
cv::Mat P1(3,4, //矩阵的大小是3x4
CV_32F, //数据类型是浮点数
cv::Scalar(0)); //初始的数值是0
//将整个K矩阵拷贝到P1矩阵的左侧3x3矩阵,因为 K*I = K
K.copyTo(P1.rowRange(0,3).colRange(0,3));
// 第一个相机的光心设置为世界坐标系下的原点
cv::Mat O1 = cv::Mat::zeros(3,1,CV_32F);
// Camera 2 Projection Matrix K[R|t]
// 计算第二个相机的投影矩阵 P2=K*[R|t]
cv::Mat P2(3,4,CV_32F);
R.copyTo(P2.rowRange(0,3).colRange(0,3));
t.copyTo(P2.rowRange(0,3).col(3));
//最终结果是K*[R|t]
P2 = K*P2;
// 第二个相机的光心在世界坐标系下的坐标
cv::Mat O2 = -R.t()*t;
//在遍历开始前,先将good点计数设置为0
int nGood=0;
// 开始遍历所有的特征点对
for(size_t i=0, iend=vMatches12.size();i<iend;i++)
{
// 跳过outliers
if(!vbMatchesInliers[i])
continue;
// Step 2 获取特征点对,调用Triangulate() 函数进行三角化,得到三角化测量之后的3D点坐标
// kp1和kp2是匹配好的有效特征点
const cv::KeyPoint &kp1 = vKeys1[vMatches12[i].first];
const cv::KeyPoint &kp2 = vKeys2[vMatches12[i].second];
//存储三维点的的坐标
cv::Mat p3dC1;
// 利用三角法恢复三维点p3dC1
Triangulate(kp1,kp2, //特征点
P1,P2, //投影矩阵
p3dC1); //输出,三角化测量之后特征点的空间坐标
// Step 3 第一关:检查三角化的三维点坐标是否合法(非无穷值)
// 只要三角测量的结果中有一个是无穷大的就说明三角化失败,跳过对当前点的处理,进行下一对特征点的遍历
if(!isfinite(p3dC1.at<float>(0)) || !isfinite(p3dC1.at<float>(1)) || !isfinite(p3dC1.at<float>(2)))
{
//其实这里就算是不这样写也没问题,因为默认的匹配点对就不是good点
vbGood[vMatches12[i].first]=false;
//继续对下一对匹配点的处理
continue;
}
// Check parallax
// Step 4 第二关:通过三维点深度值正负、两相机光心视差角大小来检查是否合法
//得到向量PO1
cv::Mat normal1 = p3dC1 - O1;
//求取模长,其实就是距离
float dist1 = cv::norm(normal1);
//同理构造向量PO2
cv::Mat normal2 = p3dC1 - O2;
//求模长
float dist2 = cv::norm(normal2);
//根据公式:a.*b=|a||b|cos_theta 可以推导出来下面的式子
float cosParallax = normal1.dot(normal2)/(dist1*dist2);
// Check depth in front of first camera (only if enough parallax, as "infinite" points can easily go to negative depth)
// 如果深度值为负值,为非法三维点跳过该匹配点对
// ?视差比较小时,重投影误差比较大。这里0.99998 对应的角度为0.36°,这里不应该是 cosParallax>0.99998 吗?
// ?因为后面判断vbGood 点时的条件也是 cosParallax<0.99998
// !可能导致初始化不稳定
if(p3dC1.at<float>(2)<=0 && cosParallax<0.99998)
continue;
// Check depth in front of second camera (only if enough parallax, as "infinite" points can easily go to negative depth)
// 讲空间点p3dC1变换到第2个相机坐标系下变为p3dC2
cv::Mat p3dC2 = R*p3dC1+t;
//判断过程和上面的相同
if(p3dC2.at<float>(2)<=0 && cosParallax<0.99998)
continue;
// Step 5 第三关:计算空间点在参考帧和当前帧上的重投影误差,如果大于阈值则舍弃
// Check reprojection error in first image
// 计算3D点在第一个图像上的投影误差
//投影到参考帧图像上的点的坐标x,y
float im1x, im1y;
//这个使能空间点的z坐标的倒数
float invZ1 = 1.0/p3dC1.at<float>(2);
//投影到参考帧图像上。因为参考帧下的相机坐标系和世界坐标系重合,因此这里就直接进行投影就可以了
im1x = fx*p3dC1.at<float>(0)*invZ1+cx;
im1y = fy*p3dC1.at<float>(1)*invZ1+cy;
//参考帧上的重投影误差,这个的确就是按照定义来的
float squareError1 = (im1x-kp1.pt.x)*(im1x-kp1.pt.x)+(im1y-kp1.pt.y)*(im1y-kp1.pt.y);
// 重投影误差太大,跳过淘汰
if(squareError1>th2)
continue;
// Check reprojection error in second image
// 计算3D点在第二个图像上的投影误差,计算过程和第一个图像类似
float im2x, im2y;
// 注意这里的p3dC2已经是第二个相机坐标系下的三维点了
float invZ2 = 1.0/p3dC2.at<float>(2);
im2x = fx*p3dC2.at<float>(0)*invZ2+cx;
im2y = fy*p3dC2.at<float>(1)*invZ2+cy;
// 计算重投影误差
float squareError2 = (im2x-kp2.pt.x)*(im2x-kp2.pt.x)+(im2y-kp2.pt.y)*(im2y-kp2.pt.y);
// 重投影误差太大,跳过淘汰
if(squareError2>th2)
continue;
// Step 6 统计经过检验的3D点个数,记录3D点视差角
// 如果运行到这里就说明当前遍历的这个特征点对靠谱,经过了重重检验,说明是一个合格的点,称之为good点
vCosParallax.push_back(cosParallax);
//存储这个三角化测量后的3D点在世界坐标系下的坐标
vP3D[vMatches12[i].first] = cv::Point3f(p3dC1.at<float>(0),p3dC1.at<float>(1),p3dC1.at<float>(2));
//good点计数++
nGood++;
//判断视差角,只有视差角稍稍大一丢丢的才会给打good点标记
//? bug 我觉得这个写的位置不太对。你的good点计数都++了然后才判断,不是会让good点标志和good点计数不一样吗
if(cosParallax<0.99998)
vbGood[vMatches12[i].first]=true;
}
// Step 7 得到3D点中较大的视差角,并且转换成为角度制表示
if(nGood>0)
{
// 从小到大排序,注意vCosParallax值越大,视差越小
sort(vCosParallax.begin(),vCosParallax.end());
// !排序后并没有取最小的视差角,而是取一个较小的视差角
// 作者的做法:如果经过检验过后的有效3D点小于50个,那么就取最后那个最小的视差角(cos值最大)
// 如果大于50个,就取排名第50个的较小的视差角即可,为了避免3D点太多时出现太小的视差角
size_t idx = min(50,int(vCosParallax.size()-1));
//将这个选中的角弧度制转换为角度制
parallax = acos(vCosParallax[idx])*180/CV_PI;
}
else
//如果没有good点那么这个就直接设置为0了
parallax=0;
//返回good点计数
return nGood;
}
六、结语
通过该篇博客的介绍,我们已经知道如何对特征点进行三角化。并且验证其三维点是否合格。如果合格我们则认为该三维点是一个正确的三维点。再结合前面的博客与代码。我们知道求解出多组 R t \mathbf R\mathbf t Rt 时,使用每组 R t \mathbf R\mathbf t Rt 对所有的特征点对进行三角化,然后选择正确三角化数量最多的一组 R t \mathbf R\mathbf t Rt 为最终解。
本文内容来自计算机视觉life ORB-SLAM2 课程课件