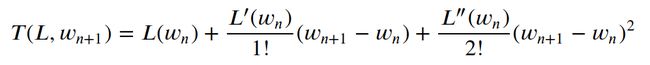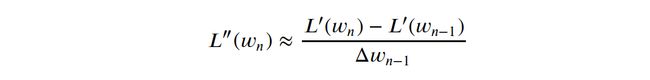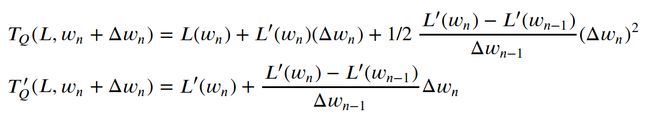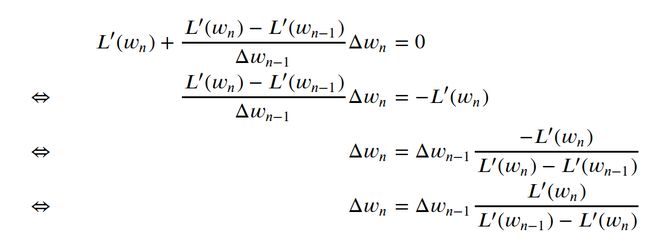反向传播方法
Due to the slowly converging nature of the vanilla back-propagation algorithms of the ’80s/’90s, Scott Fahlman invented a learning algorithm dubbed Quickprop [1] that is roughly based on Newton’s method. His simple idea outperformed back-propagation (with various adjustments) on problem domains like the ‘N-M-N Encoder’ task — i.e. training a de-/encoder network with N inputs, M hidden units and N outputs.One of the problems that Quickprop specifically tackles is the issue of finding a domain-specific optimal learning rate, or rather: an algorithm that adjusts it appropriately dynamically.
由于80年代/ 90年代香草反向传播算法的收敛特性,斯科特·法尔曼(Scott Fahlman)发明了一种称为Quickprop [1]的学习算法,该算法大致基于牛顿方法 。 他的简单想法在“ NMN编码器”任务(例如,使用N个输入,M个隐藏单元和N个输出来训练解码器/编码器网络)等问题领域上胜过反向传播(进行了各种调整)。Quickprop特别解决了其中一个问题是找到特定领域的最佳学习率的问题,或者更确切地说是:一种可以动态地对其进行适当调整的算法。
In this article, we’ll look at the simple mathematical idea behind Quickprop. We’ll implement the basic algorithm and some improvements that Fahlman suggests — all in Python and PyTorch.
在本文中,我们将研究Quickprop背后的简单数学思想。 我们将实现Fahlman建议的基本算法和一些改进-全部用Python和PyTorch进行。
A rough implementation of the algorithm and some background can already be found in this useful blog post by Giuseppe Bonaccorso. We are going to expand on that — both on the theory and code side — but if in doubt, have a look at how Giuseppe explains it.
该算法的粗略实现和一些背景知识已经可以在Giuseppe Bonaccorso的这篇有用的博客文章中找到。 我们将在理论和代码方面对此进行扩展,但是如果有疑问,请查看Giuseppe的解释方式。
The motivation to look into Quickprop came from writing my last article on the “Cascade-Correlation Learning Architecture” [2]. There, I used it to train the neural network’s output and hidden neurons, which was a mistake I realized only later and which we’ll also look into here.
探索Quickprop的动机来自撰写 我 关于“级联相关学习体系结构” [2]的 上一篇文章 。 在那里,我用它来训练神经网络的输出和隐藏的神经元,这是我后来才意识到的错误,我们还将在这里进行研究。
To follow along with this article, you should be familiar with how neural networks can be trained using back-propagation of the loss gradient (as of 2020, a widely used approach). That is, you should understand how the gradient is usually calculated and applied to the parameters of a network to try to iteratively achieve convergence of the loss to a global minimum.
要继续本文,您应该熟悉如何使用损失梯度的反向传播来训练神经网络(截至2020年,这是一种广泛使用的方法)。 也就是说,您应该了解通常如何计算梯度并将其应用于网络的参数,以尝试迭代地将损耗收敛到全局最小值。
总览 (Overview)
We’ll start with the mathematics behind Quickprop and then look at how it can be implemented and improved step by step.To make following along easier, any equations used and inference steps done are explained in more detail than in the original paper.
我们将从Quickprop背后的数学开始,然后逐步了解如何实现和改进它。为了使跟踪变得更容易,与原始论文相比,对使用的任何方程式和完成的推理步骤进行了更详细的说明。
Quickprop背后的数学 (The Mathematics Behind Quickprop)
The often used learning method of back-propagation for neural networks is based on the idea of iteratively ‘riding down’ the slop of a function, by taking short steps in the inverse direction of its gradient.
神经网络反向传播的常用学习方法是基于以下想法:迭代地“降低”函数的斜率,方法是在函数梯度的反方向上采取较短的步骤。
These ‘short steps’ are the crux here. Their length usually depends on a learning rate factor, and that is kept intentionally small to not overshoot a potential minimum.
这些“简短步骤”是这里的症结所在。 它们的长度通常取决于学习率因子,并且有意地将其保持很小,以免超出潜在的最小值。
Back in the days when Fahlman developed Quickprop, choosing a good learning rate was something of a major problem. As he actually mentions in his paper, in the best performing algorithm, the scientist chose the learning rate ‘by eye’ (i.e. manually and based on experience) every step along the way! [1]
在Fahlman开发Quickprop的时代,选择一个好的学习率是一个主要问题。 正如他在论文中实际上提到的那样,在性能最佳的算法中,科学家在整个过程中的每一步都选择了“目视”学习率(即手动并基于经验)! [1]
Faced with this, Fahlman came up with a different idea: Solving a simpler problem.
面对这一点,法曼提出了一个不同的想法:解决一个更简单的问题。
Minimizing the loss function L, especially for deep neural networks, can become extremely difficult analytically (i.e. in a general way on the entire domain).In back-propagation, for instance, we only calculate it point-wise and then do the small steps in the right direction. If we would know how the ‘terrain’ of the function looks like in general, we could ‘jump’ to the minimum directly.
最小化损失函数L尤其是对于深度神经网络,在分析上(例如,在整个域中以一般方式)可能变得极其困难。例如,在反向传播中,我们仅按点计算它,然后执行一些小步骤在正确的方向。 如果我们知道该函数的“地形”总体上看起来如何,则可以直接“跳至”最小值。
But what if we could replace the loss function with a simpler version, of which we know its terrain? This is exactly Fahlmans’ assumption taken in Quickprop: He presumes that L can be approximated by a simple parabola that opens in the positive direction. This way, calculating the minimum (of the parabola) is as simple as finding the intersection of a line with the x-axis.
但是,如果我们可以用一个更简单的版本来代替损失函数,而我们知道它的地形呢? 这正是Fahlmans在Quickprop中所采用的假设:他假设L可以由一个沿正方向打开的简单抛物线近似。 这样,计算(抛物线)的最小值就像找到一条线与x轴的交点一样简单。
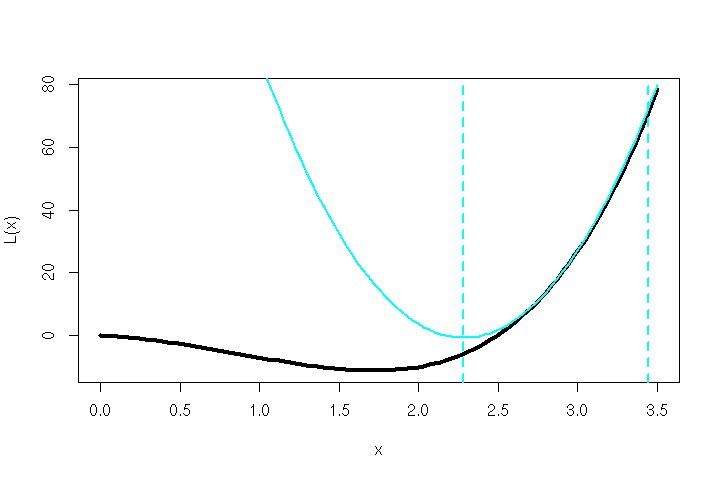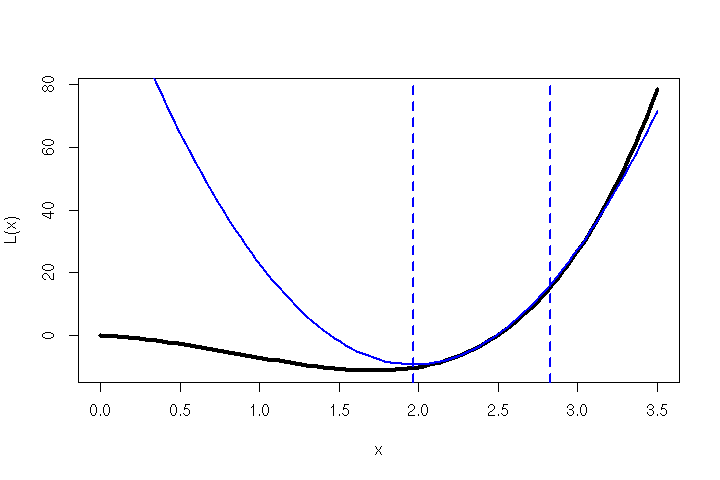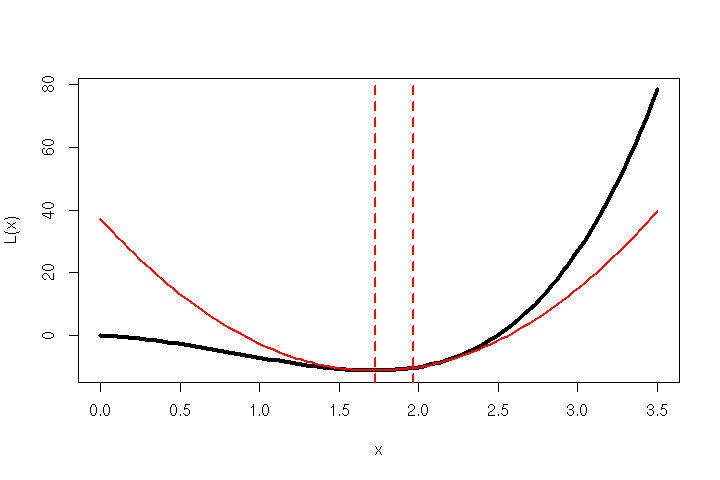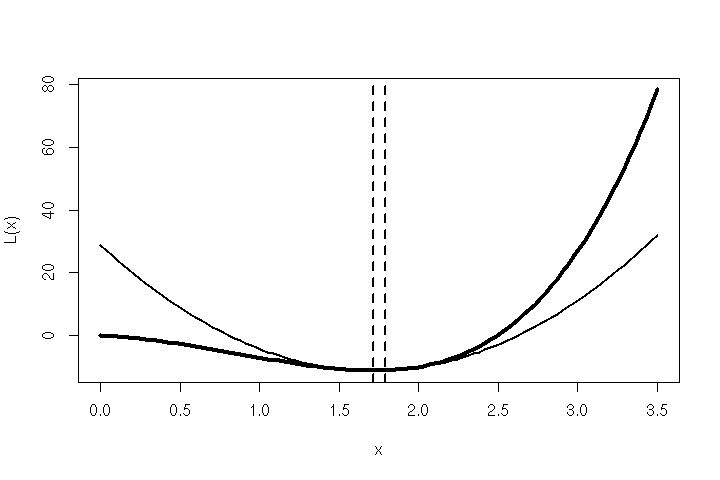
And if that point is not yet a minimum of the loss function, the next parabola can be approximated from there, like in the graphic below.
并且如果该点还不是损失函数的最小值,则可以从此处近似下一个抛物线,如下图所示。
A parabola is fit to the original function and a step is taken towards its minimum. From there, the next parabola is fit and the next step is taken. The two dotted lines are the current and a previous stationary point of the parabola. (Graphic by author) 抛物线适合原始功能,并朝其最小值迈出了一步。 从那里开始,安装下一个抛物线并采取下一步。 两条虚线是抛物线的当前点和前一个固定点。 (作者照片)So… How exactly can we approximate L? Easy — using a Taylor series, and a small trick.
那么……我们究竟如何近似得出L ? 简单-使用泰勒级数和一个小技巧。
Note that for the following equations, we consider the components of the weight vector w to be trained independently, so w is meant to be seen as a scalar. But we can still exploit the SIMD architecture of GPU’s, using component-wise computations.
请注意,对于以下方程式,我们认为权重向量 w 的分量 是独立训练的,因此 w 被视为标量。 但是我们仍然可以使用基于组件的计算来利用GPU的SIMD架构。
We start off with the second order Taylor expansion of L, giving us a parabola (without an error term):
我们从L的二阶泰勒展开式开始,给我们抛物线(无误差项):
(To understand how this was created, check out the Wikipedia article on Taylor series linked above — it’s as simple as inputting L into the general Taylor formula up to the second term and dropping the rest.)
(要了解它是如何创建的,请查看上面链接的有关Taylor系列的Wikipedia文章-就像在第二项中输入L到一般Taylor公式中一样简单,然后删除其余部分即可。)
We can now define the update rule for the weights based on a weight difference, and input that into T:
现在,我们可以基于权重差定义权重的更新规则,并将其输入到T中 :
Quickprop now further approximates L’’ linearly using the difference quotient (this is the small trick mentioned above):
Quickprop现在使用差商进一步线性近似L'' (这是上面提到的小技巧):
Using this, we can rewrite the Taylor polynomial to this ‘Quickprop’ adjusted version and build its gradient:
使用此方法,我们可以将泰勒多项式重写为此“ Quickprop”调整后的版本并建立其梯度:
And that last equation, finally, can be used to calculate the stationary point of the parabola:
最后,最后一个方程可用于计算抛物线的固定点:
That’s it! Now, to put things together, given a previous weight, a previous weight difference and the loss slope at the previous and current weight, Quickprop calculates the new weight simply by:
而已! 现在,将东西放在一起,给定先前的重量,先前的重量差以及先前和当前重量的损耗斜率,Quickprop可以通过以下方式简单地计算新的重量:
放入代码 (Putting It Into Code)
Before starting with the actual Quickprop implementation, let’s import some foundational libraries:
在开始实际的Quickprop实现之前,让我们导入一些基础库:
import numpy as np
import torchWith the last two lines of the mathematical equation from earlier, we can start with Quickprop! If you read the first article on Cascade-Correlation, you might be already familiar with this — here, we’ll concentrate on essential parts of the algorithm first, and put it all together in the end.
从前面的数学方程式的最后两行开始,我们可以开始使用Quickprop! 如果您阅读有关Cascade-Correlation的第一篇文章,您可能已经很熟悉了-在这里,我们将首先专注于算法的重要部分,最后将它们放在一起。
Note that we use PyTorch to do the automatic gradient calculation for us. We also assume to have defined an activation and loss function beforehand.
请注意,我们使用PyTorch为我们执行自动梯度计算。 我们还假设预先定义了激活和损失函数。
# Setup torch autograd for weight vector w
w_var = torch.autograd.Variable(torch.Tensor(w), requires_grad=True)
# Calc predicted values based on input x and loss based on expected output y
predicted = activation(torch.mm(x, w_var))
L = loss(predicted, y)
# Calc differential
L.backward()
# And, finally, do the weight update
dL = w_var.grad.detach() # =: partial(L) / partial(W)
dw = dw_prev * dL / (dL_prev - dL)
dw_prev = dw.clone()
w += learning_rate * dwThis is the simplest Quickprop version for one epoch of learning. To actually make use of it, we’ll have to run it several times and see if the loss converges (we’ll cover that bit later).
这是一个学习最简单的Quickprop版本。 要实际使用它,我们必须运行几次,看看损失是否收敛(稍后再介绍)。
However, this implementation is flawed in several ways, which we are going to investigate and fix in the following sections:
但是,此实现存在多种缺陷,我们将在以下几节中进行研究和修复:
We didn’t actually initialize any of the
..._prevvariables - in the last article I statically initialized them with ones, but that is also not a good idea (see next points)我们实际上并没有初始化任何
..._prev变量-在上一篇文章中,我使用了它们来静态地初始化了它们,但这也不是一个好主意(请参阅下一点)- The weight delta variable might get stuck on zero values, since it is used as a factor in its own update step 重量增量变量可能会卡在零值上,因为它被用作自己更新步骤中的一个因素
- The implementation might overshoot or generally fail to converge, if the gradient ‘explodes’ 如果坡度“爆炸”,则实现可能会超调或收敛失败
- It will result in division by zero if the gradient doesn’t change in one iteration 如果梯度在一次迭代中不发生变化,将导致除以零
改进:通过梯度下降初始化 (Improvement: Init via Gradient Descent)
The first simple fix we can apply is using gradient descent (with a very small learning rate) to prepare the dw_prev and dL_prev variables. This will give us a good first glimpse of the loss function terrain, and kick-starts Quickprop in the right direction.
我们可以应用的第一个简单解决方法是使用梯度下降(学习率非常低)来准备dw_prev和dL_prev变量。 这将使我们对损失函数的地形有一个良好的初步了解,并以正确的方向启动Quickprop。
Gradient descent is easily implemented using pytorch again — we’ll also use the opportunity to refactor the code above a bit as well:
再次使用pytorch可以轻松实现梯度下降-我们还将利用这个机会来重构上面的代码:
def calc_gradient(x, y, w, activation, loss):
# Helper to calc loss gradient
w_var = torch.autograd.Variable(torch.Tensor(w), requires_grad=True)
predicted = activation(torch.mm(x, w_var))
L = loss(predicted, y)
L.backward()
dL = w_var.grad.detach()
return L, dL, predicted
def grad_descent_step(x, y, w, activation, loss, learning_rate=1e-5):
# Calculate the gradient as usually
L, dL, predicted = calc_gradient(x, y, w, activation, loss)
# Then do a simple gradient descent step
dw = -learning_rate * dL
new_w = w + dw
return new_w, dw, L, dL改进:有条件渐变加法 (Improvement: Conditional Gradient Addition)
Sometimes, the weight deltas become vanishingly small when using the Quickprop parabola approach. To prevent that from happening when the gradient is not zero, Fahlman recommends conditionally adding the slope to the weight delta.The idea can be described like this: Go further if you have been moving in that direction anyway, but don’t push on if your previous update sent you in the opposite direction (to prevent oscillation).
有时,使用Quickprop抛物线方法时,重量增量会变得很小。 为了防止在梯度不为零时发生这种情况,Fahlman建议有条件地将权重斜率添加到权重增量中。想法可以这样描述:如果您一直沿那个方向移动,请走得更远,但如果不继续,则不要继续推您之前的更新发送给您的方向相反(以防止振荡)。
With a little piece of decider code, this can be implemented quite easily:
只需编写一些决策程序代码,就可以轻松实现:
# (This code is just to illustrate the process before the real implementation, it won't execute)
# We'll receive dw and dw_prev and need to decide whether to apply the update or not.
# To not have to include conditional execution (if clauses) we'll want to do it branchless.
# This can be achieved by a simple mutliplication rule using the sign function:
# Sign gives us either -1, 0 or 1 based on the parameter being less, more or exactly zero
# (check the docs for specifics),
np.sign(dw) + np.sign(dw_prev)
# With this, we'll have three cases as the outcome of the sum to consider here:
# -2, -1, 0, 1, 2
# But actually, we're really only interested if this is 0 or not, so we can do:
np.clip(np.abs(np.sign(dw) + np.sign(dw_prev)), a_min=0, a_max=1)
# And use that as our deciding factor, which is either 1 or 0 when the dw and dw_prev share the sign or not.With this, we can put it all into one small function:
有了这个,我们可以将其全部整合到一个小函数中:
def cond_add_slope(dw, dw_prev, dL, learning_rate=1.5):
ddw = np.clip(np.abs(np.sign(dw) + np.sign(dw_prev)), a_min=0, a_max=1)
return dw + ddw * (-learning_rate * dL)改进:最大增长因子 (Improvement: Maximum Growth Factor)
As a second step, we’ll fix the issue of exploding weight deltas near some function features (e.g. near singularities).To do that, Fahlman suggests to clip the weight update, if it would be bigger than the last weight update times a maximum grow factor:
第二步,我们将解决一些功能部件(例如奇异点)附近权重增量爆炸的问题。为此,Fahlman建议裁剪权重更新,如果它大于上次权重更新乘以最大值生长因子:
def clip_at_max_growth(dw, dw_prev, max_growth_factor=1.75):
# Get the absolute maximum element-wise growth
max_growth = max_growth_factor * np.abs(dw_prev)
# And implement this branchless with a min/max clip
return np.clip(dw, a_min=(-max_growth), a_max=max_growth)改进:防止被零除 (Improvement: Prevent Division by Zero)
On some occasions, the previous and current computed slope can be the same. The result is that we’ll try to divide by zero in the weight update rule, and will afterward continue having to work with NaN's, which obviously breaks the training.The simple fix here is to do a gradient descent step instead.
在某些情况下,先前和当前计算出的斜率可以相同。 结果是我们将尝试在权重更新规则中除以零,然后将继续使用NaN ,这显然会中断训练。此处的简单解决方法是执行梯度下降步骤。
Observe the two update rules:
遵守两个更新规则:
# Quickprop
dw = dw_prev * dL / (dL_prev - dL)
# Gradient descent
dw = -learning_rate * dL
# We'll get a nicer result if we shuffle the equations a bit:
dw = dL * dw_prev / (dL_prev - dL)
dw = dL * (-learning_rate)Besides the last factor, they look similar, no?Which means we can go branchless again (i.e. save us some if-clauses), stay element-wise and pack everything in one formula:
除了最后一个因素,它们看起来相似,不是吗?这意味着我们可以再次进入无分支(即为我们保存一些if子句),保持元素明智并将所有内容打包为一个公式:
# (This code is just to illustrate the process before the real implementation, it won't execute)
# If (dL_prev - dL) is zero, we want to multiply the learning rate instead,
# i.e. we want to switch to gradient descent. We can accomplish it this way:
# First, we make sure we only use absolute values (the 'magnitude', but element-wise)
np.abs(dL_prev - dL)
# Then we map this value onto either 0 or 1, depending on if it is 0 or not (using the sign function)
ddL = np.sign(np.abs(dL_prev - dL))
# We can now use this factor to 'decide' between quickprop and gradient descent:
quickprop_factor = ddL * (dw_prev / (dL_prev - dL))
grad_desc_factor = (1 - ddL) * (-learning_rate)
# Overall we get:
dw = dL * (quickprop_factor + grad_desc_factor)The attentive reader probably noted the ‘learning rate’ factor we used above — a parameter we thought we could get rid of…Well, actually we sort of did, or at least we did get rid of the problem of having to adjust the learning rate over the course of the training. The Quickprop learning rate can stay fixed throughout the process. It only has to be adjusted once per domain in the beginning. The actual dynamic step sizes are chosen through the parabola jumps, which in turn depend heavily on the current and last calculated slope.
细心的读者可能会注意到我们上面使用的“学习率”因素-我们认为可以摆脱的一个参数……嗯,实际上我们做了一些,或者至少我们摆脱了必须调整学习率的问题在培训过程中。 Quickprop的学习率在整个过程中可以保持不变。 开始时,每个域只需对其进行一次调整。 实际的动态步长通过抛物线跳跃来选择,而抛物线跳跃又很大程度上取决于当前和最后计算出的斜率。
If you think this sounds awfully familiar to how back-propagation learning rate optimizers work (think: momentum), you’d be on the right track. In essence, Quickprop achieves something very similar to them — just that it doesn’t use back-propagation at its core.
如果您认为这对反向传播学习率优化器的工作原理非常熟悉(认为:动量),那么您将走上正确的道路。 本质上,Quickprop实现了与它们非常相似的功能–只是它的核心没有使用反向传播。
Coming back to the code: Since we already implemented gradient descent earlier on, we can build on that and re-use as much as possible:
回到代码:由于我们早先已经实现了梯度下降,因此我们可以在此基础上进行构建并尽可能地重复使用:
def quickprop_step(x, y, w, dw_prev, dL_prev,
activation, loss,
qp_learning_rate=1.5,
gd_learning_rate=1e-5):
# Calculate the gradient as usually
L, dL, predicted = calc_gradient(x, y, w, activation, loss)
# Calculate a 'decider' bit between quickprop and gradient descent
ddL = np.ceil(np.clip(np.abs(dL_prev - dL), a_min=0, a_max=1) / 2)
quickprop_factor = ddL * (dw_prev / (dL_prev - dL))
grad_desc_factor = (1 - ddL) * (-gd_learning_rate)
dw = dL * (quickprop_factor + grad_desc_factor)
# Use the conditional slope addition
dw = cond_add_slope(dw, dw_prev, dL, qp_learning_rate)
# Use the max growth factor
dw = clip_at_max_growth(dw, dw_prev)
new_w = w + dw
return new_w, dw, L, dL, predicted放在一起 (Putting It All Together)
With all of these functions in place, we can put it all together. The bit of boilerplate code still necessary just does the initialization and checks for convergence of the mean loss per epoch.
具备所有这些功能后,我们可以将它们放在一起。 仍然需要样板代码来执行初始化,并检查每个时期的平均损耗是否收敛。
# Param shapes: x_: (n,i), y_: (n,o), weights: (i,o)
# Where n is the size of the whole sample set, i is the input count, o is the output count
# We expect x_ to already include the bias
# Returns: trained weights, last prediction, last iteration, last loss
# NB: Differentiation is done via torch
def quickprop(x_, y_, weights,
activation=torch.nn.Sigmoid(),
loss=torch.nn.MSELoss(),
learning_rate=1e-4,
tolerance=1e-6,
patience=20000,
debug=False):
# Box params as torch datatypes
x = torch.Tensor(x_)
y = torch.Tensor(y_)
w = torch.Tensor(weights)
# Keep track of mean residual error values (used to test for convergence)
L_mean = 1
L_mean_prev = 1
L_mean_diff = 1
# Keep track of loss and weight gradients
dL = torch.zeros(w.shape)
dL_prev = torch.ones(w.shape)
dw_prev = torch.ones(w.shape)
# Initialize the algorithm with a GD step
w, dw_prev, L, dL_prev = grad_descent_step(x, y, w, activation, loss)
i = 0
predicted = []
# This algorithm expects the mean losses to converge or the patience to run out...
while L_mean_diff > tolerance and i < patience:
# Prep iteration
i += 1
dL_prev = dL.clone()
w, dw, L, dL, predicted = quickprop_step(x, y, w, dw_prev, dL_prev, activation, loss, qp_learning_rate=learning_rate)
dw_prev = dw.clone()
# Keep track of losses and use as convergence criterion if mean doesn't change much
L_mean = L_mean + (1/(i+1))*(L.detach().numpy() - L_mean)
L_mean_diff = np.abs(L_mean_prev - L_mean)
L_mean_prev = L_mean
if debug and i % 100 == 99:
print("Residual ", L.detach().numpy())
print("Residual mean ", L_mean)
print("Residual mean diff ", L_mean_diff)
return w.detach().numpy(), predicted.detach().numpy(), i, L.detach().numpy()注意事项 (Caveats)
Quickprop has one major caveat that greatly reduces its usefulness: The mathematical ‘trick’ we used, i.e. the approximation of the second order derivative of the loss function with a simple difference quotient relies on the assumption that this second order derivative is a continuous function.This is not given for activation functions like e.g. the rectified linear unit, or ReLU for short. The second order-derivative is discontinuous and the behavior of the algorithm might become unreliable (e.g. it might diverge).
Quickprop有一个主要警告,它大大降低了其实用性:我们使用的数学“技巧”,即损失函数的二阶导数与简单差分商的近似依赖于以下假设:该二阶导数是连续函数。对于激活功能(例如,整流线性单元或简称ReLU)未提供此功能。 二阶导数是不连续的,算法的行为可能变得不可靠(例如,可能会发散)。
Looking back at my earlier article covering the implementation of Cascade-Correlation, we trained the hidden units of the network using Quickprop and used the covariance function as a way to estimate loss in that process. However, the covariance (as implemented there) is wrapped in an absolute value function. I.e. its second-order derivative is discontinuous and therefore, Quickprop should not be used. The careful reader of Fahlman et al.’s Cascade-Correlation paper [2] may have also noticed that they are actually using gradient ascent to calculate this maximum covariance.
回顾我之前有关级联相关性实现的文章 ,我们使用Quickprop训练了网络的隐藏单元,并使用协方差函数作为估算该过程中损失的一种方法。 但是,协方差(在此处实现)包装在绝对值函数中。 即它的二阶导数是不连续的,因此,不应使用Quickprop。 Fahlman等人的Cascade-Correlation论文[2]的细心读者也可能已经注意到,他们实际上是在使用梯度上升来计算此最大协方差。
Apart from that, it also seems that Quickprop delivers better results on some domains rather than others. An interesting summary by Brust et al. showed that it achieved better training results compared to the quality of back-propagation based techniques on some simple image classification tasks (classifying basic shapes) while at the same time doing worse on more realistic image classification tasks [3].I haven’t done any research in that direction, but I wonder if this could imply that Quickprop might work better on less fuzzy and more structured data (think data frames/tables used in a business context). That would surely be interesting to investigate.
除此之外,Quickprop在某些域上似乎比在其他域上提供了更好的结果。 Brust等人的有趣总结。 结果表明,与基于反向传播技术的质量相比,它在一些简单的图像分类任务(对基本形状进行分类)上取得了更好的训练效果,而在更逼真的图像分类任务上却表现得较差[3]。我还没有做过对此方向的任何研究,但我想知道这是否意味着Quickprop可以在较少模糊和结构化的数据上更好地工作(请考虑在业务环境中使用的数据帧/表)。 调查无疑会很有趣。
摘要 (Summary)
This article covered Scott Fahlman’s idea of improving back-propagation. We had a look at the mathematical foundations and a possible implementation.
本文介绍了斯科特·法尔曼(Scott Fahlman)改进反向传播的想法。 我们看了数学基础和可能的实现。
Now go about and try it out for your own projects — I’d love to see what Quickprop can be used for!
现在继续尝试您自己的项目-我很想看看Quickprop可以用于什么!
If you would like to see variants of Quickprop in action, check out my series of articles on the Cascade-Correlation Learning Architecture.
如果您想了解Quickprop的各种变体,请查看我关于Cascade-Correlation Learning Architecture的系列文章 。
All finished notebooks and code of this series are also available on Github. Please feel encouraged to leave feedback and suggest improvements.
Github上也提供了该系列的所有成品笔记本和代码。 请鼓励您留下反馈意见并提出改进建议。
[1] S. E. Fahlman, An empirical study of learning speed in back-propagation networks (1988), Carnegie Mellon University, Computer Science Department
[1] SE Fahlman, 反向传播网络中学习速度的实证研究 (1988年),卡内基梅隆大学,计算机科学系
[2] S. E. Fahlman and C. Lebiere, The cascade-correlation learning architecture (1990), Advances in neural information processing systems (pp. 524–532)
[2] SE Fahlman和C. Lebiere, 级联相关学习体系结构 (1990年),神经信息处理系统的进展(第524-532页)。
[3] C. A. Brust, S. Sickert, M. Simon, E. Rodner and J. Denzler, Neither Quick Nor Proper — Evaluation of QuickProp for Learning Deep Neural Networks (2016), arXiv preprint arXiv:1606.04333
[3] CA Brust,S。Sickert,M。Simon,E。Rodner和J. Denzler,《 既不快速也不正确—评估用于学习深度神经网络的QuickProp》 (2016年),arXiv预印本arXiv:1606.04333
翻译自: https://towardsdatascience.com/quickprop-an-alternative-to-back-propagation-d9a78069e2a7
反向传播方法