商空间的理解（Quotient space）

商空间（Quotient space）

In linear algebra, the quotient space of a vector space $V$ by a subspace $N$ is a vector spapce obtained by “collapsing” $N$ to zero. The space obtained is called a quotient space and is denoted $V/N$ (read “V mod N” or “V by N”).

定义

令$V$是数域$\mathbb{F}$上的矢量空间(vector space)，$N$是$V$的子空间，即$N\subseteq V$。我们定义矢量空间$V$上的等价相关(equivalence relation $\sim$)，写为：$x\sim y$ if $x-y\in N$（That is $x$ is related to $y$ if one can be obtained from the other by adding an element of $N$）。根据该定义，我们可以推断出：any element of $N$ is related to $0$。更确切地说，$N$中的所有向量都映射到零向量的等价类(equivalent class)中。

The equivalence class (or in this case, the coset) of $x$ is often denoted:
$$[x]=x+N$$

具体的形式：
$$[x]=\{x+n:n\in N\}$$

The quotient space $V/N$ is then defined as $V/\sim$, the set of all equivalence classes induced by $\sim$ on $V$.

Scalar multiplication and addition are defined on the equivalence classes by:
$$\begin{array}{rl}\alpha [x]& =[\alpha x]\forall \alpha \in \mathbb{F}\\ [x]+[y]& =[x+y]\end{array}$$

证明：
（1）齐次性
$$\alpha [x]\iff \alpha [x]=\{\alpha (x+n):n\in N\}\iff \{\alpha x+n:n\in N\}\iff [\alpha x]$$

（2）叠加性
$$[x]+[y]\iff \{(x+n_1)+(y+n_2):n_1,n_2\in N\}\iff \{x+y+n:n_1,n_2\in N\}\iff [x+y]$$

这些线性操作使商空间$V/N$变成了数域$\mathbb{F}$上的一个矢量空间，只是我们需要注意该矢量空间的元素不是一个向量，而是一个等价类。并且我们不难得到，子空间$N$为”0类“（zero class），即
$$N=[0]$$

The mapping that associates to $v\in V$ the equivalence calss $[v]$ is known as quotient map (商映射)
商映射即定义为$v\in V$与等价类$[v]$的映射。

强调

！！商空间首先是一个集合，这个集合里边有很多元素，里边的每个元素是一个等价类。如果在商空间上定义函数，那么函数的定义域就是一个等价类，即商空间中的一个元素。另外，可以把商空间$V/N$理解为数域$\mathbb{F}$上的一个矢量空间，只是我们需要注意该矢量空间的元素不是一个向量，而是一个等价类。

举例

例子-1

令$X={\mathbb{R}}^2$来表示标准笛卡尔平面(Cartesian plane)，令$Y$为$X$中穿过原点的一条直线，那么商空间$X/Y$就是$X$中所有与$Y$平行的线（This is to say that, the elements of the set $X/Y$ are lines in $X$ in parallel to $Y$）。Note that the points along any one such line will satisfy the equivalence relation because their difference vectors belong to $Y$. (<= this gives a way to visualize quotient spaces geometrically.)
对这句话的直观理解如下图所示

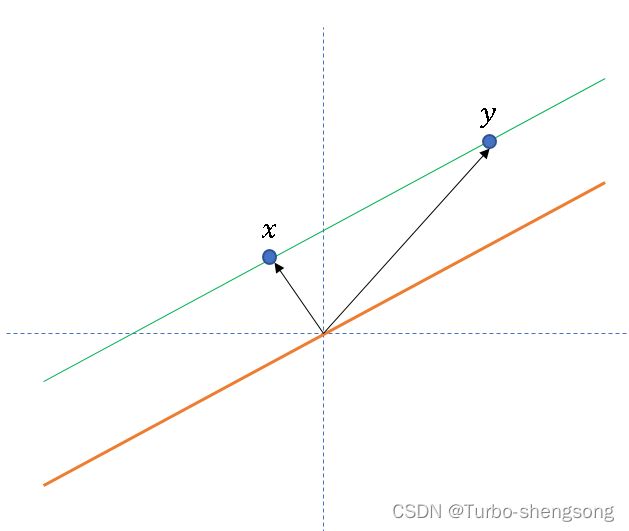
直观地理解，上面所描述的商空间就是一个集合，这个集合里的任意一个元素就是与$Y$平行的直线。

例子-2

我们考虑矢量空间${\mathbb{R}}^n$与其中一个子空间（例如：m standard basis vectors）的商空间。我们将矢量空间与子空间描述为：

• The space ${\mathbb{R}}^n$ consists of all n-tuples of real numbers $(x_1,\cdots ,x_n)$
• The subspace, identified with ${\mathbb{R}}^m$, consists of all $n-$tuples such that the last $n-m$ entries are zero: $(x_1,\cdots ,x_m,0,\cdots ,0)$

不难得到：
$$\mathbf{x}\sim \mathbf{y}(\mathbf{x},\mathbf{y}\in {\mathbb{R}}^n)\iff \text{ they are identical in the last }n-m\text{ coordinates}$$

另外，商空间${\mathbb{R}}^n/{\mathbb{R}}^m$与矢量空间${\mathbb{R}}^{n-m}$同构（因为商空间${\mathbb{R}}^n/{\mathbb{R}}^m$中的每一个元素/等价类内部的所有向量，最后的$n-m$个元素都相同，那么商空间${\mathbb{R}}^n/{\mathbb{R}}^m$中的每个元素与矢量空间${\mathbb{R}}^{n-m}$中的每个向量都一一对应（单射），并且对应到整个$(n-m)$维矢量空间，从而满足满射，所以两个空间的映射关系为双射，因此两个空间同构）。

商空间的性质

从例子-2中，我们可以直接得到：
$$dim(V/U)=dim(V)-dim(U)$$

(后续相关的性质，之后需要的时候再更新)

参考

[1] CSDN上关于商空间的其他介绍
[2] 维基百科