Chapter3 Pytorch神经网络工具箱

利用Pytorch神经网络工具箱，设计一个神经网网络就像搭积木一样，可以极大的简化我们构建模型的任务。在此介绍如何使用Pytorch神经网络工具箱来构建网络，主要有以下内容:

• 神经网络核心组件
• nn模块中的Module和functional
• 神经网络中的层、块和模型
• 神经网络中的参数管理
• 优化器以及优化器的比较
• 如何构建一个神经网络
• 保存和加载模型
• GPU

1、神经网络核心组件

神经网络看起来很复杂，节点很多，层数多，参数更多。但核心部分或组件不多，把这些组件确定之后，这个神经网络就基本确定了，这些核心组件包括：

1. 层：神经网络的基本结构，将输入张量转换为输出张量
2. 模型：层构成的网络
3. 损失函数：参数学习的目标函数，通过最小化损失函数来学习各种参数。
4. 优化器：如何使损失函数最小，设计优化器。

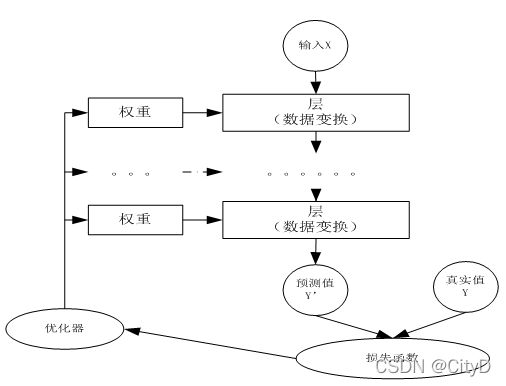
这些组件之间不是独立的，他们之间，以及它们与神经网络其他组件之间有密切关系。这些关键组件及相互关系，如下图所示。

多个层链接在一起构成一个模型或网络，输入数据通过这个模型转换为预测值，然后损失函数把预测值与真实值进行比较，得到损失值，该损失函数值用于衡量预测值与目标结果的匹配或相似程度，优化器利用损失值更新权重参数，从而使损失值越来越小。这是一个循环过程，当损失值达到一个阈值或循环次数到达指定次数，循环结束。

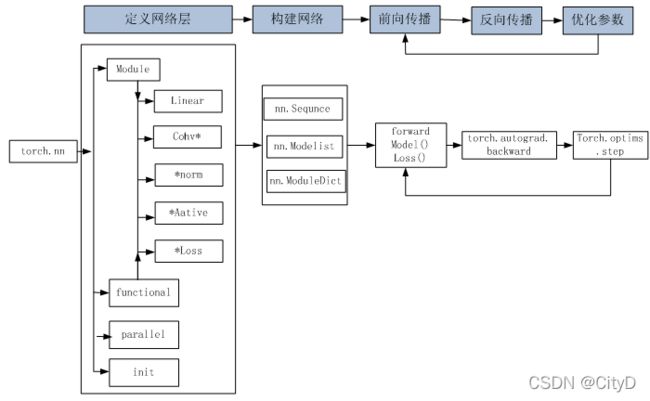
使用Pytorch构建神经网络使用的主要工具(或类)及相互关系，如下图所示。

2、nn模块中的Module和functional

nn模块中有两个重要模块:nn.Model、nn.functional。构建网络层可以基于Module类或函数(nn.functional)。nn.functional中函数与nn.Module中的Layer的主要区别是后者继承Module类，会自动提取可学习的参数。而nn.functional更像是纯函数。两者功能相同，且性能也没有很大的区别，那么应该如何选择？像卷积层、全连接层、Dropout层等因含有可学习参数，一般使用nn.Module;而激活函数、池化层不含可学习参数，可以使用nn.functional中对应的函数。

2.1、nn.Module

nn.Module是nn的一个核心数据结构，它可以是神经网络的某个层(Layer)，也可以是包含多层的神经网络。在实际使用中，最常见的做法是继承nn.Module，生成自己的网络/层。nn中已实现了绝大多数层，包括全连接层、损失层、激活层、卷积层、循环层等，这些层都是nn.Module的子类，能够自动检测到自己的Parameter，并将其作为学习参数，且针对GPU进行了cuDNN优化。

2.2、nn.functional

nn中的层，一类是继承了nn.Module，其命名一般为nn.Xxx(第一个为大写)，如nn.Linear、nn.Conv2d、nn.CrossEntropyLoss等。另一类是nn.functional中的函数，其名称一般为nn.functional.xxx，如nn.functional.linear、nn.functional.conv2d、nn.functional.cross_entropy等。从功能来说两者相当，且性能没有太大差异。在具体使用时，两者还是有区别，主要区别如下：

1. nn.Xxx继承于nn.Module，nn.Xxx需要先实例化并传入参数，然后以函数调用的方式调用实例化的对象并传入输入数据。它能够很好地与nn.Sequential结合使用，而nn.functional.xxx无法与nn.Sequential结合使用。
2. nn.Xxx不需要自己定义和管理weight、bias参数；而nn.functional.xxx需要自己定义weight、bias参数，每次调用的时候都需要手动传入weight、bias等参数，不利于代码复用。
3. Dropout操作在训练和测试阶段是有区别的，使用nn.Xxx方式定义Dropout，在调用model.eval()之后，自动实现状态的转换，而使用nn.functional.xxx没有该功能。

Pytorch官方推荐:具有学习参数的(例如，conv2d,linear,batch_norm)采用nn.Xxx方式。没有学习参数的(例如，maxpool、loss func、activation func)等根据个人选择使用nn.functional.xxx或nn.Xxx的方式。

2.3、Sequential()使用介绍

Sequential()函数的功能是将网络的层组合到一起，功能与Keras的models.Sequential()类似，构建网络就像搭积木一样，十分的方便。下面使用Sequential()函数构建一个多层的多层感知机网络，有关Sequential()函数是如何实现的可看3.3节。

import torch
from torch import nn

net=nn.Sequential(nn.Linear(4,8),nn.ReLU(),
                 nn.Linear(8,8),nn.ReLU(),
                 nn.Linear(8,1))
X=torch.rand(2,4)
net(X),net

(tensor([[-0.3123],
         [-0.3337]], grad_fn=),
 Sequential(
   (0): Linear(in_features=4, out_features=8, bias=True)
   (1): ReLU()
   (2): Linear(in_features=8, out_features=8, bias=True)
   (3): ReLU()
   (4): Linear(in_features=8, out_features=1, bias=True)
 ))

如果要对每个层定义一个名称，可以采用Sequential的一种改进方法，在Sequential的基础上，通过add_module()添加每一层，并且为每一层添加一个单独的名字。

net=nn.Sequential()
net.add_module('linear1',nn.Linear(4,8))
net.add_module('activate1',nn.ReLU())
net.add_module('linear2',nn.Linear(8,8))
net.add_module('activate2',nn.ReLU())
net.add_module('linear3',nn.Linear(8,1))
X=torch.rand(2,4)
net(X),net

(tensor([[-0.1616],
         [-0.1190]], grad_fn=),
 Sequential(
   (linear1): Linear(in_features=4, out_features=8, bias=True)
   (activate1): ReLU()
   (linear2): Linear(in_features=8, out_features=8, bias=True)
   (activate2): ReLU()
   (linear3): Linear(in_features=8, out_features=1, bias=True)
 ))

另一种方法实在Sequential的基础上，通过字典的形式添加每一层，并且设置单独的层名称，以下是采用字典方式构建网络的一个示例代码:

#子类OrderedDict，实现了对字典对象中元素的排序
#使用OrderedDict会根据放入元素的先后顺序进行排序
from collections import OrderedDict
class Net(nn.Module):
    def __init__(self):
        super(Net,self).__init__()
        self.block=nn.Sequential(
            OrderedDict([
                ("dense1",nn.Linear(4,8)),
                ("relu1",nn.ReLU()),
                ("dense2",nn.Linear(8,8)),
                ("relu2",nn.ReLU()),
                ("dense3",nn.Linear(8,1))
            ])
        )
    def forward(self,X):
        return self.block(X)
net=Net()
X=torch.rand(2,4)
net(X),net

(tensor([[0.1490],
         [0.1656]], grad_fn=),
 Net(
   (block): Sequential(
     (dense1): Linear(in_features=4, out_features=8, bias=True)
     (relu1): ReLU()
     (dense2): Linear(in_features=8, out_features=8, bias=True)
     (relu2): ReLU()
     (dense3): Linear(in_features=8, out_features=1, bias=True)
   )
 ))

2.4、使用nn.Module和nn.functional构建MLP模型

import torch
from torch import nn
import torch.nn.functional as F
class Net(nn.Module):
    def __init__(self,in_dim,n_hidden_1, n_hidden_2,out_dim):
        super(Net,self).__init__()
        #Sequential()函数的功能是将网络的层组合到一起
        #线性层和batchNorm使用nn.Module
        self.layer1=nn.Sequential(nn.Linear(in_dim,n_hidden_1),nn.BatchNorm1d(n_hidden_1))
        self.layer2=nn.Sequential(nn.Linear(n_hidden_1,n_hidden_2),nn.BatchNorm1d(n_hidden_2))
        self.layer3=nn.Sequential(nn.Linear(n_hidden_2,out_dim))
    def forward(self,x):
        #激活函数使用nn.functional
        x=F.relu(self.layer1(x))
        x=F.relu(self.layer2(x))
        x=self.layer3(x)
        return x
#实例化网络，参数为个层的节点数
net=Net(2,3,3,1)
print(net)

Net(
  (layer1): Sequential(
    (0): Linear(in_features=2, out_features=3, bias=True)
    (1): BatchNorm1d(3, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  )
  (layer2): Sequential(
    (0): Linear(in_features=3, out_features=3, bias=True)
    (1): BatchNorm1d(3, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  )
  (layer3): Sequential(
    (0): Linear(in_features=3, out_features=1, bias=True)
  )
)

3、神经网络中的层、块和模型

对于单一输出的线性模型只有一个神经元组成。单个神经元(1)接受一些输入；(2)生成相应的标量输出；(3)具有一组相关参数，这些参数可以以优化某些感兴趣的目标函数。对于多个输出的网络也可以由上述进行描述。在使用线性模型的时候，一个单层本身就是模型。

而对于多层感知机而言，整个模型及其组成层都是这种结构。整个模型接受原始输入(特征)，生成输出(预测)，并包含一些参数(所有组成层的参数集合)。同样每个单独的层接受输入(由前一层提供)生成输出(到下一层)，并且具有一组可调参数，这些参数根据从下一层反向传播的信号进行更新。

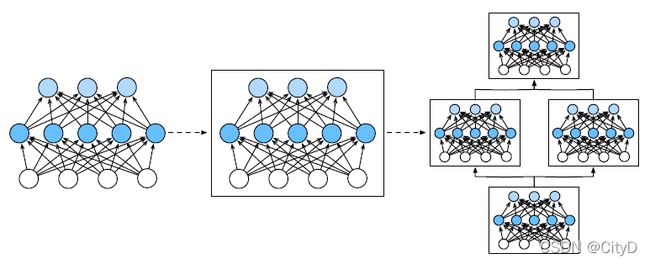
虽然神经元、层和模型为我们的业务提供了足够的抽象，但讨论“比单个层⼤”但“比整个模型小”的组件更有价值。计算机视觉中流行的ResNet-152架构有数百层，这些层是由层组的重复模式组成。层组以各种重复模式排列的类似架构在现在是普遍存在的。为了实现这些复杂的网络，我们引入了神经网络块的概念。块可以描述单个层、由多个层组成的组件或者整个模型本身。通过定义代码来按需生成任意复杂度的块，可以通过简洁的代码实现复杂的神经网络。

从编程的角度看，块由类表示，它的任何子类都必须定义一个将其输入转换为输出的前向传播函数，并且必须存储任何必须必的参数。由于自动微分实现了反向传播，因此我们只需要考虑前向传播和必须的参数。

下面是一个多层感知机的代码。代码构成一个网络，其中包含一个具有256个单元的ReLU激活函数的全连接层的隐藏层，然后是一个具有10个隐藏单元且不带激活层的全连接层的输出层。

import torch
from torch import nn
from torch.nn import functional as F

#构建网络
net = nn.Sequential(nn.Linear(20,256),nn.ReLU(),nn.Linear(256,10))

#输出张量
X=torch.randn(2,20)

#输出
net(X)

tensor([[-0.1556,  0.1318, -0.3911,  0.0676,  0.1655,  0.0950, -0.2956,  0.0608,
          0.6323, -0.1332],
        [ 0.1199,  0.2001, -0.2833,  0.2620, -0.0786, -0.1871,  0.0011,  0.3654,
          0.1516, -0.1067]], grad_fn=)

在本例中，通过实例化nn.Sequential来构建模型。nn.Sequential定义了一种特殊的Module。

3.1、自定义层

深度学习可以用创造性的方式组合广泛的层，从而设计出适用于各种任务的结构，因此需要自己去构建深度学习框架中还不存在的层。

3.1.1、不带参数的层

首先构建一个没有任何参数的层，下面的CenterLayer类实现从其输入中减去均值。需要继承基础层类并实现正向传播功能。

import torch
import torch.nn.functional as F
from torch import nn

class CenteredLayer(nn.Module):
    def __init__(srlf):
        super().__init__()
    def forward(self,X):
        return X-X.mean()      

提供一些数据验证该层是否可以按预期工作。

#定义对象
layer=CenteredLayer()
#将输入传入层，获得输出
layer(torch.FloatTensor([1,2,3,4,5]))

tensor([-2., -1.,  0.,  1.,  2.])

可以将层作为组件合并到更复杂的模型中。

net=nn.Sequential(nn.Linear(8,128),CenteredLayer())

传入数据，检查是否可以运行。

Y=net(torch.rand(4,8))
Y.mean()

tensor(5.5879e-09, grad_fn=)

3.1.2、带参数的层

继续定义一个有参数的层，，这些参数可以通过训练进行调整。我们可以使用内置函数来创建参数，这些函数提供⼀些基本的管理功能。比如管理访问、初始化、共享、保存和加载模型参数。这样做的好处之⼀是：我们不需要为每个自定义层编写自定义的序列化程序。

实现一个自定义版本的全连接层。该层需要权重和偏置两个参数。使用ReLU作为激活函数。该层需要两个输入in_units和units，分别表示输入和输出的数量。

class MyLinear(nn.Module):
    def __init__(self,in_units,units):
        super().__init__()
        #Parameter:首先可以把这个函数理解为类型转换函数，
        #将一个不可训练的类型Tensor转换成可以训练的类型parameter
        #并将这个parameter绑定到这个module里面
        self.weight=nn.Parameter(torch.randn(in_units,units))
        self.bias=nn.Parameter(torch.randn(units,))
    def forward(self,X):
        #matmul:张量相乘
        linear=torch.matmul(X,self.weight.data)+self.bias.data
        return F.relu(linear)

实例化MyLinear类并访问其模型参数。

linear=MyLinear(5,3)
linear.weight

Parameter containing:
tensor([[ 1.1091,  1.4573, -0.8924],
        [ 0.0896, -1.4303, -0.0430],
        [-0.9766,  0.1827,  0.4117],
        [-1.1084,  0.5383,  0.1812],
        [ 0.4216, -0.0934,  0.1748]], requires_grad=True)

使用自定义的层直接执行正向传播计算。

linear(torch.rand(2,5))

tensor([[0.0000, 0.2072, 0.8235],
        [0.0000, 0.0000, 1.6173]])

还可以使用自定义层构建模型。可以像使用内置的全连接成一样使用自定义层。

net=nn.Sequential(MyLinear(64,8),MyLinear(8,1))
net(torch.rand(2,64))

tensor([[0.],
        [0.]])

3.2、自定义块

要想直观了解块是如何工作的，最简单的方法就是自己实现一个。每个块必须提供的基本功能如下。

1. 将输入数据作为其正向传播函数的参数。
2. 通过正向传播函数生成输出。
3. 计算其输出关于输入的梯度，可以通过反向传播函数实现，通常是自动进行的。
4. 存储和访问正向传播计算所需的参数。
5. 根据需要初始化模型参数。

从零开始编写一个块。它包含一个多层感知机，其具有256个隐藏单元的隐藏层和一个10维输出层。下面的MLP类继承了表示块的类(nn.Module)。因此只需要提供自己的构造函数(Python中的__init__函数)和前向传播函数。

import torch
from torch import nn
from torch.nn import functional as F

class MLP(nn.Module):
    #定义模型的层，声明两个全连接的层
    def __init__(self):
        #初始化父类
        super().__init__()
        self.hidden=nn.Linear(20,256)#隐藏层
        self.out=nn.Linear(256,10)#输出层
    #定义正向传播，可以根据输出X返回模型的输出
    def forward(self,X):
        #使用ReLU激活函数
        return self.out(F.relu(self.hidden(X)))

我们定制的__init__函数通过super().__init__() 调用父类的__init__函数，省去了重复编写模版代码的痛苦。然后，我们实例化两个全连接层，分别为self.hidden和self.out。注意，除⾮我们实现⼀个新的运算符，否则不必担心反向传播函数或参数初始化，系统将自动生成这些。

X=torch.rand(2,20)
net=MLP()
net(X)

tensor([[-0.1003,  0.1205,  0.1990,  0.0434,  0.2265,  0.2731, -0.2046, -0.0733,
          0.1833,  0.3483],
        [-0.2320,  0.1059,  0.2352, -0.1212,  0.2700,  0.1981, -0.1899, -0.1203,
          0.0759,  0.3010]], grad_fn=)

抽象块的一个优点是它的多功能性。可以子类化块以创建层、整个模型或具有中等复杂度的各种组件。

3.3、顺序块(Sequential类)

为了更清楚的了解Sequential类是如何工作的，下面构建自己简化的MySequential，只需要定义两个关键函数：1.一种将块逐个追加到列表的函数。2.一种正向传播函数，用于将输入按追加块的顺序传递给块组成的“链条”。

import torch
from torch import nn
from torch.nn import functional as F

class MySequential(nn.Module):
    def __init__(self,*args):
        super().__init__()
        for block in args:
            #这里 block是Module子类的一个实例。将其保存在Module类的成员变量_modules中。block的类型是OrderedDict
            self._modules[block]=block
    def forward(self,X):
        #OrderedDict保证了按照成员添加的顺序遍历他们
        for block in self._modules.values():
            X=block(X)
        return X

每个Module都有一个_modules属性。使用它而不使用自己定义的python的列表是因为_modules在块的初始化过程中，系统知道在_modules字典中查找需要初始化参数的子块。

当MySequential的正向传播函数被调用时，每个添加的块都按照他们被添加的顺序执行。

net=MySequential(nn.Linear(20,256),nn.ReLU(),nn.Linear(256,10))
X=torch.rand(2,20)
net(X)

tensor([[ 0.0995,  0.0281, -0.0389,  0.0936,  0.0438,  0.2560,  0.2108, -0.1924,
          0.0846, -0.1313],
        [ 0.0511,  0.0070, -0.0647,  0.0691,  0.0067,  0.3497,  0.2170, -0.1781,
         -0.0008, -0.2260]], grad_fn=)

3.4、在正向传播中执行代码

并不是所有的架构都是简单的顺序结构。当需要更大的灵活性时，我们需要自定义块。例如，在正向传播函数中执行python的控制流。此外可能希望执行任意的数学运算，而不是简单的依赖预定义的神经网络层。下面实现了FixedHiddenMLP类。

import torch
from torch import nn
from torch.nn import functional as F

class FixedHiddenMLP(nn.Module):
    def __init__(self):
        super().__init__()
        #不计算梯度的随机权重参数，在训练期间保持不变
        self.rand_weight=torch.rand((20,20),requires_grad=False)
        self.linear=nn.Linear(20,20)
    def forward(self,X):
        X=self.linear(X)
        #使用创建的常量参数以及relu和dot函数
        X=F.relu(torch.mm(X,self.rand_weight)+1)
        #复用全连接层，两个全连接成共享参数
        X=self.linear(X)
        #控制流
        while X.abs().sum()>1:
            X/=2
        return X.sum()

没有标准的神经网络可以执行上述操作。下面查看是否可以实现该网络。

net=FixedHiddenMLP()
X=torch.rand(2,20)
net(X)

tensor(0.1608, grad_fn=)

还可以混合搭配各种组合块的方法。下面的例子中，实现方法嵌套块。

class NestMLP(nn.Module):
    def __init__(self):
        super().__init__()
        self.net=nn.Sequential(nn.Linear(20,64),nn.ReLU(),nn.Linear(64,32),nn.ReLU())
        self.linear=nn.Linear(32,16)
    def forward(self,X):
        return self.linear(self.net(X))
chimera=nn.Sequential(NestMLP(),nn.Linear(16,20),FixedHiddenMLP())
X=torch.rand(2,20)
chimera(X)

tensor(-0.1679, grad_fn=)

4、神经网络中的参数管理

有时，我们希望提取参数，以便在其他环境中复用他们，将模型保存到磁盘，以便它可以再其他软件中执行，或者为了获得科学的理解而进行检查。因此介绍以下内容：

• 访问参数，用于调试、诊断和可视化
• 参数初始化
• 在不同的模型组件中共享参数

首先定义一个具有单隐藏层的多层感知机。

import torch
from torch import nn

net=nn.Sequential(nn.Linear(4,8),nn.ReLU(),nn.Linear(8,1))
X=torch.rand(size=(2,4))
net(X)

tensor([[0.4796],
        [0.5347]], grad_fn=)

4.1、参数访问

从已有的模型中访问参数。当通过Sequential类定义模型时，可以通过索引来访问模型的任意层。模型就像一个列表。每层的参数都在其属性中。如下所示，可以检查第二个全连接层的参数。

print(net[2].state_dict())

OrderedDict([('weight', tensor([[ 0.2000,  0.3015,  0.2418, -0.0520, -0.0950,  0.1996,  0.1854, -0.0726]])), ('bias', tensor([0.3100]))])

这个全连接层包含两个参数，分别是该层的权重和偏置。

目标参数

下面的代码从第二个神经网络层提取偏置，提取后返回的是一个参数类实例，并进一步访问该参数。

print(type(net[2].bias))
print(net[2].bias)
print(net[2].bias.data)

Parameter containing:
tensor([0.3100], requires_grad=True)
tensor([0.3100])

参数是复合对象，包含值、梯度和额外信息。

除了值之外，还可以访问每个参数的梯度。由于还没有调用网络的反向传播，所以参数的梯度处于初始状态。

print(net[2].weight.grad)

None

一次性访问所有参数

使用递归整个树来提取每个子块的参数。

#获取第0层的参数
print(*[(name,param.shape) for name,param in net[0].named_parameters()])
#获取第所有层的参数，因为第二层是relu层，因此没有参数
print(*[(name,param.shape) for name,param in net.named_parameters()])

('weight', torch.Size([8, 4])) ('bias', torch.Size([8]))
('0.weight', torch.Size([8, 4])) ('0.bias', torch.Size([8])) ('2.weight', torch.Size([1, 8])) ('2.bias', torch.Size([1]))

还有另一种访问网络参数的方式

net.state_dict()['2.bias'].data

tensor([0.3100])

从嵌套块收集参数

让多个块相互嵌套，参数命名约定是如何工作的。为此定义一个生成块，然后将这些组合到更大的块中。

def block1():
    return nn.Sequential(nn.Linear(4,8),nn.ReLU(),
                        nn.Linear(8,4),nn.ReLU())
def block2():
    net=nn.Sequential()
    for i in range(4):
        #嵌套,并给块命名
        net.add_module(f'block{i}',block1())
    return net
rgnet = nn.Sequential(block2(),nn.Linear(4,1))
X=torch.rand(size=(2,4))
rgnet(X)

tensor([[0.2028],
        [0.2029]], grad_fn=)

查看网络是如何组织的

print(rgnet)

Sequential(
  (0): Sequential(
    (block0): Sequential(
      (0): Linear(in_features=4, out_features=8, bias=True)
      (1): ReLU()
      (2): Linear(in_features=8, out_features=4, bias=True)
      (3): ReLU()
    )
    (block1): Sequential(
      (0): Linear(in_features=4, out_features=8, bias=True)
      (1): ReLU()
      (2): Linear(in_features=8, out_features=4, bias=True)
      (3): ReLU()
    )
    (block2): Sequential(
      (0): Linear(in_features=4, out_features=8, bias=True)
      (1): ReLU()
      (2): Linear(in_features=8, out_features=4, bias=True)
      (3): ReLU()
    )
    (block3): Sequential(
      (0): Linear(in_features=4, out_features=8, bias=True)
      (1): ReLU()
      (2): Linear(in_features=8, out_features=4, bias=True)
      (3): ReLU()
    )
  )
  (1): Linear(in_features=4, out_features=1, bias=True)
)

因为层是分层嵌套的，可以像通过嵌套列表索引一样访问他们。例如访问第一个主要的块，其中第二个子块的第一层的偏置项。

rgnet[0][1][0].bias.data

tensor([-0.1297, -0.2927,  0.2727, -0.4982,  0.2166,  0.3460, -0.0646,  0.4258])

4.2、参数初始化

深度学习框架提供默认随机初始化。然而，我们希望可以根据其他规则初始化权重。深度学习框架提供了最常用的规则，也允许自定义初始化方法。

默认情况下，Pytorch会根据一个范围均匀地初始化权重和偏置矩阵，这个范围是根据输入和输出维度计算出的。Pytorch的nn.init模块提供了多种预置的初始化方法。

4.2.1、内置初始化

首先使用内置的初始化器。下面的代码将所有权重参数初始化为标准差为0.01的高斯随机变量，且将偏置参数设置为0。

def init_normal(m):
    if type(m)==nn.Linear:
        nn.init.normal_(m.weight,mean=0,std=0.01)
        nn.init.zeros_(m.bias)
#网络为上一节定义
net.apply(init_normal)
net[0].weight.data[0],net[0].bias.data[0]

(tensor([-4.3025e-03,  2.7619e-03, -8.0229e-03, -5.2681e-05]), tensor(0.))

还可以将所有参数初始化为给定的常数

def init_constant(m):
    if type(m)==nn.Linear:
        nn.init.constant_(m.weight,1)
        nn.init.zeros_(m.bias)
net.apply(init_constant)
net[0].weight.data[0],net[0].bias.data[0]

(tensor([1., 1., 1., 1.]), tensor(0.))

4.2.2、自定义初始化

下面例子中，使用以下的分布为任意权重参数$w$定义初始化方法：

$$w\sim \{\begin{array}{ll}U(5,10),& \text{with probability 1/4 }\\ 0,& \text{with probability 1/2}\\ U(-10,-5),& \text{with probability 1/4}\end{array}$$

def my_init(m):
    if type(m)==nn.Linear:
        print("Init",*[(name,param.shape) for name,param in m.named_parameters()][0])
        nn.init.uniform_(m.weight,-10,10)
        m.weight.data*=m.weight.data.abs()>=5
net.apply(my_init)
net[0].weight[:2]

Init weight torch.Size([8, 4])
Init weight torch.Size([1, 8])





tensor([[ 0.0000,  0.0000,  5.1294, -8.5471],
        [-8.3953,  7.2347, -7.2256, -0.0000]], grad_fn=)

4.3、参数绑定

有时我们希望在多个层之间共享参数，下面定义一个稠密层，然后使用它的参数来设置另一个层的参数。其实就是使用同一个层。

#我们需要给共享层一个参数，以便可以引用它的参数。
shared=nn.Linear(8,8)

net=nn.Sequential(nn.Linear(4,8),nn.ReLU(),
                 shared,nn.ReLU(),
                 shared,nn.ReLU(),
                 nn.Linear(8,1))
X=torch.rand(size=(2,4))
net(X)
#检查参数是否相同
print(net[2].weight.data[0]==net[4].weight.data[0])
net[2].weight.data[0,0]=100
print(net[2].weight.data[0]==net[4].weight.data[0])

tensor([True, True, True, True, True, True, True, True])
tensor([True, True, True, True, True, True, True, True])

5、优化器以及优化器的比较

Pytorch常用的优化器都封装在torch.optim里面，设计灵活，可以扩展为自定义的优化方法。所有的优化方法都继承了基类optim.Optimizer，并实现了自己的优化步骤。最常用的优化算法就是梯度下降法及其各种变种。

5.1、优化器使用步骤

1. 建立优化器实例

导入optim模块，实例化优化器，根据需要选择合适的优化器，这里以动量版的SGD为例

import torch.optim as optim
#model.parameters()为模型的参数,lr为学习率,monentum为动量
optimizer=optim.SGD(model.parameters(),lr=lr,monentum=momentum)

2. 前向传播

把输入数据传入神经网络Net实例化对象model中，自动执行forward函数，得到out输出值，然后用out与标记label计算损失值loss。

out=model(img)
loss=criterion(out,label)

3. 清空梯度

缺省情况下梯度是累加的，在梯度反向传播前，先需把梯度清零。

optimizer.zero_grad()

4. 反向传播

基于损失值，把梯度进行反向传播

loss.backward()

5. 更新参数

基于当前梯度(存储在参数的.grad属性中)更新参数。

optimizer.step()

5.2、修改学习率参数

修改优化器中参数的方式可以修改参数optimizer.params_groups。

optimizer.params_groups：长度为1的list；optimizer.params_groups[0]：长度为6的字典，包括权重参数、lr、momentum等参数。

len(optimizer.param_groups[0]) #结果为6

可以通过修改optimizer.param_groups[0]['lr']的值修改学习率。

5.3、优化器比较

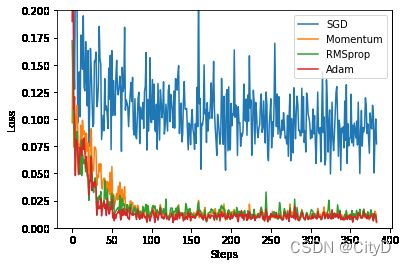
Pytorch中优化器很多，各种优化器都有其适应的场景，不过自适应优化器在深度学习中比较受欢迎，有性能好、鲁棒性、泛化能力强的优点。下面使用多种优化器实现网络。有SGD、SGD的动量版、RMSProp、Adam。

1. 导入所需要的模块。

import torch
import torch.utils.data as data
import torch.nn.functional as F
import matplotlib.pyplot as plt
%matplotlib inline

#超参数
#学习率
LR=0.01
#批量大小
BATCH_SIZE=32
#训练轮次
EPOCH=12

2. 生成数据

#生成数据的函数
def synthetic_data(num_example):
    #生成-1到1区间内的num_example个数据
    x=torch.linspace(-1,1,num_example)
    #将一维变二维，torch智能处理二维的数据
    x=torch.unsqueeze(x,dim=1)
    #生成y，并添加噪声
    y=x.pow(2)+0.1*torch.normal(torch.zeros(*x.size()))
    return x,y
x,y=synthetic_data(1000)
#构造一个Pytorch数据迭代器
def load_array(data_arrays,batch_size,is_train=True):
    #加星号说明为元组
    #TensorDataset 可以用来对 tensor 进行打包
    dataset=data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset,batch_size,shuffle=is_train)
loader=load_array((x,y),BATCH_SIZE)

3. 构建神经网络

class Net(torch.nn.Module):
    def __init__(self):
        super(Net,self).__init__()
        self.hidden=torch.nn.Linear(1,20)
        self.predict=torch.nn.Linear(20,1)
    def forward(self,x):
        x=F.relu(self.hidden(x))
        x=self.predict(x)
        return x

4. 使用多种优化器

#SGD
net_SGD=Net()
#Momentum
net_Momentum=Net()
#RMSProp
net_RMSProp=Net()
#Adam
net_Adam=Net()

nets=[net_SGD,net_Momentum,net_RMSProp,net_Adam]

#设置优化器
opt_SGD=torch.optim.SGD(net_SGD.parameters(),lr=LR)
opt_Momentum=torch.optim.SGD(net_Momentum.parameters(),lr=LR,momentum=0.9)
opt_RMSProp=torch.optim.RMSprop(net_RMSProp.parameters(),lr=LR,alpha=0.9)
opt_Adam=torch.optim.Adam(net_Adam.parameters(),lr=LR,betas=(0.9,0.99))

optimizers=[opt_SGD,opt_Momentum,opt_RMSProp,opt_Adam]

5. 训练模型

#设置损失函数
loss_func=torch.nn.MSELoss()
#记录损失
loss_his=[[],[],[],[]]

#训练模型
for epoch in range(EPOCH):
    #每次去BATCH_SIZE条数据，直到对所有数据取完
    for step,(batch_x,batch_y) in enumerate(loader):
        #对使用不同的优化器的网络进行训练
        #zip用于将可迭代对象作为参数,将对象中对应的元素打包成一个个元组,然后返回由这些元组组成的对象。
        for net,opt,l_his in zip(nets,optimizers,loss_his):
            #得到预测值
            output=net(batch_x)
            #计算损失
            loss=loss_func(output,batch_y)
            #清空梯度
            opt.zero_grad()
            #反向传播
            loss.backward()
            #更新参数
            opt.step()
            #记录损失
            l_his.append(loss.data.numpy())
labels=['SGD','Momentum','RMSprop','Adam']            

6. 可视化结果

for i,l_his in enumerate(loss_his):
    plt.plot(l_his,label=labels[i])
plt.legend(loc='best')
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.ylim((0,0.2))
plt.show()

​

​

6、如何构建一个神经网络

构建神经网络的步骤：

1. 构建网络层，使用nn.Sequential、nn.Module、nn.funcational根据实际情况搭建模型
2. 前向传播，主要定义froward函数。主要任务是将输入层，网络层，输出层连接起来，实现信息的前向传播。
3. 反向传播，Pytorch提供了自动反向传播的功能，使用nn工具箱，无语自己编写反向传播，直接让损失函数loss调用backwrd()即可。在反向传播中，优化器是一个重要角色，需要根据实际情况选择合适的优化器。
4. 模型训练，模型训练时，要注意使模型处于训练模式，即调用model.train()。调用model.train()会把所有的module设置为训练模式。如果是测试或验证阶段，需要使模型处于验证阶段，即调用model.eval()，调用model.eval()会把所有的training属性设置为False。缺省情况下梯度是累加的，调用optimizer.zero_grad()将梯度初始化或清零。训练过程中，正向传播生成网络的输出，计算输出和实际值之间的损失值。调用loss.backward()自动生成梯度，然后使用optimizer.step()执行优化器，把梯度传会并更新参数。也可以使用GPU进行网络的训练。

7、保存和加载模型

介绍保存和加载张量和模型参数

7.1、加载和保存张量

对于单个张量，可以直接调用load和save函数分别读取他们。这两个函数都要求我们提供一个名称，save要求将要保存的变量作为输入。

import torch
from torch import nn
from torch.nn import functional as F

x=torch.arange(4)
print(x)
#保存张量
torch.save(x,'x-file')

tensor([0, 1, 2, 3])

现在可以从存储文件中的数据读回内存。

x2=torch.load('x-file')
x2

tensor([0, 1, 2, 3])

可以存储一个张量列表，然后把他们读回内存。

y=torch.zeros(4)
torch.save([x,y],'xy-files')
x2,y2=torch.load('xy-files')
(x2,y2)

(tensor([0, 1, 2, 3]), tensor([0., 0., 0., 0.]))

还可以写入或读取从字符串映射到张量的字典

mydict={'x':x,'y':y}
torch.save(mydict,'mydict')
mydict2=torch.load('mydict')
mydict2

{'x': tensor([0, 1, 2, 3]), 'y': tensor([0., 0., 0., 0.])}

7.2、加载和保存模型参数(官方推荐)

深度学习框架提供了内置函数来保存和加载整个网络。需要注意的是，这将保存模型的参数而不是保存整个模型。因此在恢复模型的时候，需要用代码生成结构，然后从磁盘加载参数。

#构建一个多层感知机
class MLP(nn.Module):
    def __init__(self):
        super(MLP,self).__init__()
        self.hidden=nn.Linear(20,256)
        self.output=nn.Linear(256,10)
    def forward(self,x):
        return self.output(F.relu(self.hidden(x)))
net=MLP()
X=torch.rand(size=(2,20))
Y=net(X)

将模型的参数保存到一个叫“mlp.params”的文件中。

torch.save(net.state_dict(),"mlp.params")

为了恢复模型，我们实例化原始多层感知机的一个备份。没有随机初始化模型参数，而是直接读取文件中存储的参数。

clone=MLP()
clone.load_state_dict(torch.load('mlp.params'))
clone.eval()

MLP(
  (hidden): Linear(in_features=20, out_features=256, bias=True)
  (output): Linear(in_features=256, out_features=10, bias=True)
)

由于两个实例具有相同的模型参数，在输入相同的X时，两个实例的计算结果应该相同。

Y_clone=clone(X)
Y_clone==Y

tensor([[True, True, True, True, True, True, True, True, True, True],
        [True, True, True, True, True, True, True, True, True, True]])

7.3、加载和保存整个模型(模型+参数)

首先构建一个模型。

import torch
from torch import nn
from torch.nn import functional as F
#构建一个多层感知机

class MLP(nn.Module):
    def __init__(self):
        super(MLP,self).__init__()
        self.hidden=nn.Linear(20,256)
        self.output=nn.Linear(256,10)
    def forward(self,x):
        return self.output(F.relu(self.hidden(x)))
net=MLP()
X=torch.rand(size=(2,20))
net(X)

tensor([[ 0.0579, -0.0811,  0.1751,  0.0401,  0.1001, -0.1680,  0.0061, -0.1768,
         -0.0621, -0.1509],
        [ 0.1113,  0.0192,  0.1754, -0.0482,  0.0619, -0.0059,  0.1285, -0.1294,
         -0.0634,  0.0177]], grad_fn=)

保存整个模型:

torch.save(net,'mlp.pkl')

加载保存的整个模型，陷阱(加载的时候，必须引入模型所定义的类，否则会报错):

net2=torch.load('mlp.pkl')
net2,net2(X)

(MLP(
   (hidden): Linear(in_features=20, out_features=256, bias=True)
   (output): Linear(in_features=256, out_features=10, bias=True)
 ),
 tensor([[ 0.0579, -0.0811,  0.1751,  0.0401,  0.1001, -0.1680,  0.0061, -0.1768,
          -0.0621, -0.1509],
         [ 0.1113,  0.0192,  0.1754, -0.0482,  0.0619, -0.0059,  0.1285, -0.1294,
          -0.0634,  0.0177]], grad_fn=))

可见模型和网络均被保存了下来，使用加载的模型处理相同的数据，输出和原来的模型的输出是相同的。

8、GPU

GPU的发展已经到了较为成熟的阶段。利用GPU来训练深度神经网络，可以充分利用其计算核心的能力。提高深度神经网络的训练速度。Pytorch支持GPU，可以通过to(device)函数来将数据从内存转移到GPU显存上。Pytorch一般把GPU作用于张量(Tensor)或模型(包括torch.nn下面的一些网络模型以及自己创建的模型)等数据结构上。

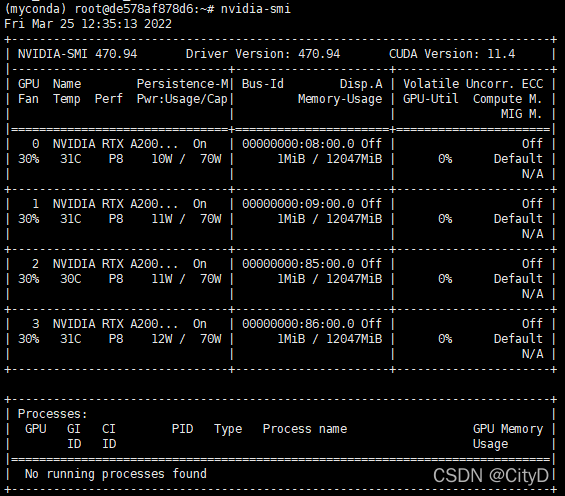
在使用GPU之前，需要确保至少安装了一个NVIDIA GPU。然后下载NVIDIA驱动和CUDA并按照提示设置适当的路径。当准备工作完成后，就可以使用nvidia-smi命令查看显卡信息。

在使用GPU之前，需要确保GPU是可用的，可以通过torch.cuda.is_available()方法的返回值进行判断。

import torch

torch.cuda.is_available()

True

8.1、计算设备

在Pytorch中，CPU和GPU可以用torch.device('cpu')和torch.cuda.device('cuda')表示。如果有多个GPU，可以使用torch.cuda.device(f'cuda:{i}')来表示第$i$块GPU。另外，cuda:0和cuda是等价的。

import torch
from torch import nn

torch.device('cpu'),torch.cuda.device('cuda'),torch.cuda.device('cuda:1')

(device(type='cpu'),
 ,
 )

可以利用下面的方法查询可用GPU的数量。

torch.cuda.device_count()

1

下面定义两个函数，这两个函数允许在请求GPU不存在的情况下运行代码。

#如果存在，则返回gpu(i)，否则返回cpu
def try_gpu(i=0):
    if torch.cuda.device_count()>=i+1:
        return torch.device(f'cuda:{i}')
    return torch.device('cpu')
#返回所有可用的gpu,如果没有gpu,则返回cpu
def try_all_gpus():
    devices=[torch.device(f'cuda:{i}') for i in range(torch.cuda.device_count())]
    return devices if devices else [torch.device('cpu')]

try_gpu(),try_gpu(10),try_all_gpus()

(device(type='cuda', index=0),
 device(type='cpu'),
 [device(type='cuda', index=0)])

8.2、张量与GPU

在默认情况下，张量是在CPU上创建的，我们可以查询张量所在的设备。

x=torch.tensor([1,2,3])
x.device

device(type='cpu')

如果对多个项进行操作，那么它们都必须在同一个设备上。需要确保需要操作的两个张量都位于同一个设备上，否则不知道在哪里存储结果，甚至不知道在哪里执行计算。

存储在GPU上

有几种方法可以再GPU上存储张量，一种是在创建张量的时候指定存储设备；另一种是在创建完张量之后将其放到GPU上。下面介绍这两种方法。

1. 在创建张量的时候指定存储设备。

X=torch.ones(2,3,device=torch.device("cuda:0" if torch.cuda.is_available() else "cpu"))
#还可以这样写
XX=torch.ones(2,3).cuda(0)
X,XX

(tensor([[1., 1., 1.],
         [1., 1., 1.]], device='cuda:0'),
 tensor([[1., 1., 1.],
         [1., 1., 1.]], device='cuda:0'))

也可以使用刚才定义的方法

X1=torch.ones(2,3,device=try_gpu())
X1

tensor([[1., 1., 1.],
        [1., 1., 1.]], device='cuda:0')

2. 创建张量之后将其放到GPU上，使用.to(device)方法

import torch
X2=torch.ones(2,3)
X2.to(try_gpu())
X2.device

device(type='cpu')

按理说是可以的！！！，之后研究下在更新。

假设至少有两个GPU，下面的代码将在第二个GPU上运行，我的电脑没有~~~~。所以被放到了cpu上。

Y=torch.rand(2,3,device=try_gpu(1))
Y,Y.device

(tensor([[0.7841, 0.2906, 0.4341],
         [0.6017, 0.4530, 0.0363]]),
 device(type='cpu'))

X,Y存在不用的设备上，如果直接执行X+Y，将会报错，因此需要将X和Y放到同一个设备上才能正常运行。

X+Y

---------------------------------------------------------------------------

RuntimeError                              Traceback (most recent call last)

~\AppData\Local\Temp/ipykernel_2192/2223898888.py in 
----> 1 X+Y


RuntimeError: Expected all tensors to be on the same device, but found at least two devices, cuda:0 and cpu!

Z=Y.cuda(0)
print(Y)
print(Z)
#然后执行X+Z
X+Z

tensor([[0.7841, 0.2906, 0.4341],
        [0.6017, 0.4530, 0.0363]])
tensor([[0.7841, 0.2906, 0.4341],
        [0.6017, 0.4530, 0.0363]], device='cuda:0')





tensor([[1.7841, 1.2906, 1.4341],
        [1.6017, 1.4530, 1.0363]], device='cuda:0')

8.3、神经网络与GPU

类似地，神经网络也可以指定设备。下面的代码将模型参数放到GPU上。

net1 = nn.Sequential(nn.Linear(3,1))
net2 = nn.Sequential(nn.Linear(3,1))
net3 = nn.Sequential(nn.Linear(3,1))
#1.使用定义的方法
net1=net1.to(device=try_gpu())
#2.使用if判断
net2=net2.to(device=torch.device("cuda:0" if torch.cuda.is_available() else "cpu"))
#3.使用.cuda
net3=net3.cuda(0)
net1,net2,net3

(Sequential(
   (0): Linear(in_features=3, out_features=1, bias=True)
 ),
 Sequential(
   (0): Linear(in_features=3, out_features=1, bias=True)
 ),
 Sequential(
   (0): Linear(in_features=3, out_features=1, bias=True)
 ))

当输入也为GPU上的张量时，模型将在同一GPU上计算结果

X=torch.ones(2,3,device=try_gpu())
net1(X),net2(X),net3(X)

(tensor([[-0.9122],
         [-0.9122]], device='cuda:0', grad_fn=),
 tensor([[-0.2564],
         [-0.2564]], device='cuda:0', grad_fn=),
 tensor([[-0.0785],
         [-0.0785]], device='cuda:0', grad_fn=))

确认模型参数存储在同一个GPU上

net1[0].weight.data.device

device(type='cuda', index=0)