神经网络初级学习（Python代码实现）

运行结果：

 

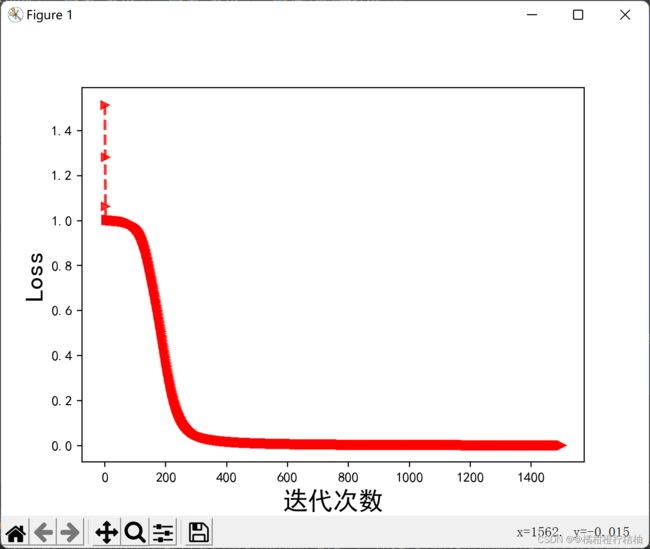
Python代码实现 ：

# coding=gbk

#====导入相关库==========

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体
#mpl.rcParams['font.sans-serif'] = ['Times New Roman'] #Times New Roman字体
mpl.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题
import matplotlib; matplotlib.use('TkAgg')


# 激活函数
def sigmoid(x):
    return 1.0 / (1 + np.exp(-x))

#
def sigmoid_derivative(x):
    return x * (1.0 - x)

# 计算损失函数
def compute_loss(y_hat, y):
    return ((y_hat - y)**2).sum()

class NeuralNetwork:
    def __init__(self, x, y):
        self.input = x
        # 它为每个输入创建 4 个介于 0 和 1 之间的随机数
        self.weights1 = np.random.rand(self.input.shape[1], 4)
        self.weights2 = np.random.rand(4, 1)
        self.y = y
        self.output = np.zeros(self.y.shape)

    def feedforward(self):
        self.layer1 = sigmoid(np.dot(self.input, self.weights1))
        self.output = sigmoid(np.dot(self.layer1, self.weights2))

    def backprop(self):
        # application of the chain rule to find derivative of the loss function with respect to weights2 and weights1
        d_weights2 = np.dot(self.layer1.T, (2 * (self.y - self.output) * sigmoid_derivative(self.output)))
        d_weights1 = np.dot(self.input.T, (np.dot(2 * (self.y - self.output) * sigmoid_derivative(self.output),
                                                  self.weights2.T) * sigmoid_derivative(self.layer1)))

        # update the weights with the derivative (slope) of the loss function
        self.weights1 += d_weights1
        self.weights2 += d_weights2


if __name__ == "__main__":
    #===特征=======
    X = np.array([[0, 0, 1],
                  [0, 1, 1],
                  [1, 0, 1],
                  [1, 1, 1]])
    #====目标======
    y = np.array([[0], [1], [1], [0]])
    nn = NeuralNetwork(X, y)

    loss_values = [] # 记录loss列表
    for i in range(1500):
        nn.feedforward()
        nn.backprop()
        loss = compute_loss(nn.output, y) # 计算loss
        loss_values.append(loss)

print(nn.output) # 输出
print(f" final loss : {loss}") # 最终loss
# 可视化loss变化
plt.plot(loss_values,color='red',marker='>',linestyle='--',linewidth=2,alpha=0.8,label='loss')
plt.xlabel('迭代次数',fontsize=18) #fontsize=18 调整字大小
plt.ylabel('Loss',fontsize=18)
plt.show()

# coding=gbk

#====导入相关库==========

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体
#mpl.rcParams['font.sans-serif'] = ['Times New Roman'] #Times New Roman字体
mpl.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题
import matplotlib; matplotlib.use('TkAgg')


# 激活函数
def sigmoid(x):
    return 1.0 / (1 + np.exp(-x))

#
def sigmoid_derivative(x):
    return x * (1.0 - x)

# 计算损失函数
def compute_loss(y_hat, y):
    return ((y_hat - y)**2).sum()

class NeuralNetwork:
    def __init__(self, x, y):
        self.input = x
        # 它为每个输入创建 4 个介于 0 和 1 之间的随机数
        self.weights1 = np.random.rand(self.input.shape[1], 4)
        self.weights2 = np.random.rand(4, 1)
        self.y = y
        self.output = np.zeros(self.y.shape)

    def feedforward(self):
        self.layer1 = sigmoid(np.dot(self.input, self.weights1))
        self.output = sigmoid(np.dot(self.layer1, self.weights2))

    def backprop(self):
        # application of the chain rule to find derivative of the loss function with respect to weights2 and weights1
        d_weights2 = np.dot(self.layer1.T, (2 * (self.y - self.output) * sigmoid_derivative(self.output)))
        d_weights1 = np.dot(self.input.T, (np.dot(2 * (self.y - self.output) * sigmoid_derivative(self.output),
                                                  self.weights2.T) * sigmoid_derivative(self.layer1)))

        # update the weights with the derivative (slope) of the loss function
        self.weights1 += d_weights1
        self.weights2 += d_weights2


if __name__ == "__main__":
    #===特征=======
    X = np.array([[0, 0, 1],
                  [0, 1, 1],
                  [1, 0, 1],
                  [1, 1, 1]])
    #====目标======
    y = np.array([[0], [1], [1], [0]])
    nn = NeuralNetwork(X, y)

    loss_values = [] # 记录loss列表
    for i in range(1500):
        nn.feedforward()
        nn.backprop()
        loss = compute_loss(nn.output, y) # 计算loss
        loss_values.append(loss)

print(nn.output) # 输出
print(f" final loss : {loss}") # 最终loss
# 可视化loss变化
plt.plot(loss_values,color='red',marker='>',linestyle='--',linewidth=2,alpha=0.8,label='loss')
plt.xlabel('迭代次数',fontsize=18) #fontsize=18 调整字大小
plt.ylabel('Loss',fontsize=18)
plt.show()

# coding=gbk

#====导入相关库==========

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体
#mpl.rcParams['font.sans-serif'] = ['Times New Roman'] #Times New Roman字体
mpl.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题
import matplotlib; matplotlib.use('TkAgg')


# 激活函数
def sigmoid(x):
    return 1.0 / (1 + np.exp(-x))

#
def sigmoid_derivative(x):
    return x * (1.0 - x)

# 计算损失函数
def compute_loss(y_hat, y):
    return ((y_hat - y)**2).sum()

class NeuralNetwork:
    def __init__(self, x, y):
        self.input = x
        # 它为每个输入创建 4 个介于 0 和 1 之间的随机数
        self.weights1 = np.random.rand(self.input.shape[1], 4)
        self.weights2 = np.random.rand(4, 1)
        self.y = y
        self.output = np.zeros(self.y.shape)

    def feedforward(self):
        self.layer1 = sigmoid(np.dot(self.input, self.weights1))
        self.output = sigmoid(np.dot(self.layer1, self.weights2))

    def backprop(self):
        # application of the chain rule to find derivative of the loss function with respect to weights2 and weights1
        d_weights2 = np.dot(self.layer1.T, (2 * (self.y - self.output) * sigmoid_derivative(self.output)))
        d_weights1 = np.dot(self.input.T, (np.dot(2 * (self.y - self.output) * sigmoid_derivative(self.output),
                                                  self.weights2.T) * sigmoid_derivative(self.layer1)))

        # update the weights with the derivative (slope) of the loss function
        self.weights1 += d_weights1
        self.weights2 += d_weights2


if __name__ == "__main__":
    #===特征=======
    X = np.array([[0, 0, 1],
                  [0, 1, 1],
                  [1, 0, 1],
                  [1, 1, 1]])
    #====目标======
    y = np.array([[0], [1], [1], [0]])
    nn = NeuralNetwork(X, y)

    loss_values = [] # 记录loss列表
    for i in range(1500):
        nn.feedforward()
        nn.backprop()
        loss = compute_loss(nn.output, y) # 计算loss
        loss_values.append(loss)

print(nn.output) # 输出
print(f" final loss : {loss}") # 最终loss
# 可视化loss变化
plt.plot(loss_values,color='red',marker='>',linestyle='--',linewidth=2,alpha=0.8,label='loss')
plt.xlabel('迭代次数',fontsize=18) #fontsize=18 调整字大小
plt.ylabel('Loss',fontsize=18)
plt.show()