论文翻译-Learning Deep Network Representations with Adversarially
利用对抗性正则化自编码器学习深层网络表示
- 摘要
- 暂时没时间整理公式,后面有时间改公式
- 1 绪论
- 2 准备工作
-
- 2.1 自动编码器神经网络
- 2.2 生成对抗网络
- 2.3 网络嵌入
- 3 途径
-
- 3.1 随机生成器
- 3.2 反向正则化自动编码器的嵌入
- 4 评估
-
- 4.1 数据集
- 4.2 比较算法
- 4.3 可视化
- 4.4 链路预测
- 4.5 网络重构
- 4.6 多标记分类
- 4.7 参数敏感性
- 5 相关工作
- 6 结论
- 鸣谢
- 参考文献
- 总结与体会
WenchaoYu1,ChengZheng1,WeiCheng2,CharuC.Aggarwal3,DongjinSong2,BoZong2, HaifengChen2,andWeiWang1
1加州大学洛杉矶分校计算机科学系
2NEC美国实验室公司
3IBM AI研究部
{wenchaoyu,chengzheng,weiwang}@cs.ucla.edu,{weicheng,bzong,dsong,haifeng}@nec-labs.com,[email protected]
摘要
网络表示学习的问题,也称为网络嵌入,产生于许多学习任务,假设在顶点表示中存在少量可变性,这些可变性可以捕获原始网络结构的“语义”。具有浅层或深层体系结构的模型,从低维嵌入、局部可重构性和全局可重构性中学习顶点表示从输入网络中取样的序列。同样地,通过学习概率密度函数和取样序列来处理生成顶点表示的问题。然而,由于输入网络采样序列的固有稀疏性,所得到的结果很难在形式上加以推广。因此,通过学习概率密度泛函数在样本序列上生成顶点表示来处理问题。在本研究中,我们建议学习使用反向正则化自编码器(NETRA)的网络表示。NETRA学习了通过联合考虑局部性和全局重构约束来捕获结构的描述。我们实证地演示了网络结构的关键特性是如何被捕获的,以及NETRA在多种任务上的有效性,包括网络重构、链路预测和多标签分类。
关键词:网络嵌入、自动编码器、通用对抗网络
暂时没时间整理公式,后面有时间改公式
1 绪论
网络分析在挖掘有用信息方面具有巨大的潜力,这些有用信息对诸如链接预测、社区检测和社会网络异常检测[34]、生物网络[31]和语言网络[28]、语言网络等下游任务有利。
在分析工作数据时,一个基本的问题是超顶点的低维向量表示,即网络结构被应用到向量空间[23]。问题是,有两个主要挑战:(1)复杂结构性质的保持。嵌入网络的目的在于“适合”训练网络,从而保留网络的结构性质[23,26]。然而,这个复合体的潜在结构却以概率密度的显式形式表现出来,而这种概率密度又能反映局部网络邻域信息和全局网络结构。(2)网络抽样的稀疏性。目前主要采用抽样技术,包括随机游走抽样、广度优先搜索等,来导出约束数据集的外部序列。然而,抽样只占全部顶点序列的很小一部分。另一种方法是构造连续码空间[37]。不幸的是,由于在许多情况下,在低维流形中可能不存在先验分布,因此学习连续离散案例的潜在表示仍然是一个具有挑战性的问题[26]。
近来,网络嵌入在复杂网络的顶点表示方面取得了长足的进展[23,26,37]。这些表示采用非线性变换来捕捉原始网络的“语义”。大多数表示方法首先采用从输入网络开始的遍历,然后建立具有最优允许维顶点嵌入顺序的模型。由于顶点序列的总数非常大,因此采样策略会遇到数据稀疏问题。随后,在稀疏样本集上的学习倾向于产生一个过于复杂的模型来解释采样数据集,最终导致过拟合。流形仍是不相关流形。理想情况下,可以用单重分布实现连续的顶点表示。然而,在很多情况下,在低维流形中,先验分布的形式是不确定的、不可能的、完全定义的。例如,Dai等人[6]建议训练鉴别器来辨别。由固定的先验分布和输入编码产生的区别的样本,并由此将嵌入分布推向固定的先验分布。虽然它具有更大的灵活性,但是它受到模型崩溃问题的困扰[16]。此外,大多数具有深结构的模型通常不考虑先验分布。采样的顶点序列的顶点信息[37]。因此,不能很好地考虑邻近的信息。
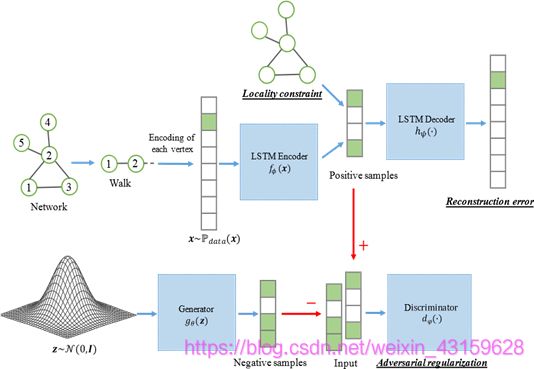
为解决上述问题,在本研究中,我们提出了一个新的模型,它用逆规则描述子(NETRA)来表示,NETRA联合地将局部保持最小化,并把自编码器的构造误差与短期记忆法(LSTM)结合起来。将输入序列映射到固定长度表示的编码器。联合推理用于对抗性训练过程,以避开重复优先分配的要求。如图1所示,我们的模型使用离散LSTM自动编码器来学习控制该模型不仅使LSTM自编码器的构造误差最小化,而且使LSTM自编码器中的局部保持损失也同时减小。生成性对抗训练可以作为网络嵌入过程的补充规则器。
NETRA具有网络嵌入模型所要求的不可分割性:1)结构特性保持,NETRA利用了网络拓扑结构之间的LSTM,以及网络拓扑结构的特征。2)泛化能力,泛化能力,等同于泛化能力,使分布和人口之后的非顶点序列得以生成。明确密度分布克服了输入顶点之间的矛盾。实验结果表明网络重构、链路预测和多标签分类等算法具有较强的嵌入能力。综上所述,本工作的主要贡献如下:
我们利用生成对抗训练过程,通过联合最小化局部保持损失和全局重构误差,提出了一种具有通用规则零树编码NETRA的深度网络嵌入模型。
从网络上看,NETRA学会了从离散输入中产生有用的顶点表示,而不需要定义间接隐含空间先验知识。
我们利用真实世界信息网络进行了网络重构、链接预测和多标记分类的广泛实验。实验结果表明NETRA的有效性和高效性。
在第二节中,我们回顾了自编码器、生成对抗网络和网络嵌入算法的初步知识。在第三节,我们描述了利用生成对抗过程学习低维映射的NETRA框架。通过网络重构、链路预测、多标签分类等联合框架,实现了NETRA的性能。在第五节中,我们比较了NETRA框架和其他网络嵌入算法,讨论了相关的工作,最后,在第六节中,我们总结并提出了未来工作的方向。
2 准备工作
2.1 自动编码器神经网络
训练自动编码器神经网络以将目标值设置为等于输入。网络由两部分组成:编码器f_ϕ (·),用于将输入(x∈R^n)映射到潜在的低维表示,以及解码器h_ψ (·),用于产生输入的重建。具体来说,给定一个数据分布P_data,从中得出x,即x~P_data (x),我们想学习表示f_ϕ (x),使得输出假设h_ψ 〖(f〗_ϕ (x))近似等于x。学习过程简单地描述为最小化成本函数,
minE_(x~P_data (x)) [dist(x,h_ψ (f_ϕ (x)))], (1)
dist(·)是数据空间中的某种相似性度量。在实践中,距离测量有很多选择。例如,如果我们使用l2范数来测量重建误差,那么目标函数可以定义为L_LE(φ,ψ;x)= E_(x~P_data (x) ) ||x-h_ψ (f_ϕ (x)))〖||〗^2。类似地,交叉熵损失的目标函数可以定义为,
-E_(x~P_data (x) ) [xlogh_ψ (f_ϕ (x))+(1-x)log(1-h_ψ (f_ϕ (x)))], (2)
编码器f_ϕ (·)和解码器h_ψ (·)的选择可能因不同的任务而异。在本文中,我们使用LSTM自动编码器[27],它能够处理序列作为输入。
2.2 生成对抗网络
生成对抗网络(GANs)[11]为两个玩家建立一个对抗训练平台,即生成器g_θ (·)和鉴别器d_w (·),以进行极小极大值游戏。
■(min@θ)■(max@w)■(E@x~P_data (x))[logd_w (x)]+■(E@z~P_g (z))[log(1-d_w (g_θ (z)))] (3)
发生器g_θ (·)试图将噪声映射到输入空间,使数据更接近,而鉴别器d_w (x)则表示从数据到噪声的概率,其目的是区分真实数据分布P_data (x)和伪样本分布P_g (z),如z~N(0,I)。Wasserstein GANs [1]用Earth-Mover距离(Wasserstein-1)代替Jensen-Shannon发散,克服了训练不稳定的问题,解决了这个问题。
■(min@θ)■(max@wϵW)■(E@x~P_data (x))[d_w (x)]-■(E@z~P_g (z))[d_w (g_θ (z))] (4)
通过截断判别器的权重,在连续空间[-c,c]中保持了判别器上的Lipschitz约束W。
2.3 网络嵌入
网络嵌入方法寻求学习编码关于网络的结构信息的表示。这些方法学习了将顶点嵌入到低维空间中的映射。给定编码顶点集{x((1)),…,x((n))},找到每个x^((i))的嵌入f_ϕ (x^((i) ) )可以形式化为最优化问题[39,41],
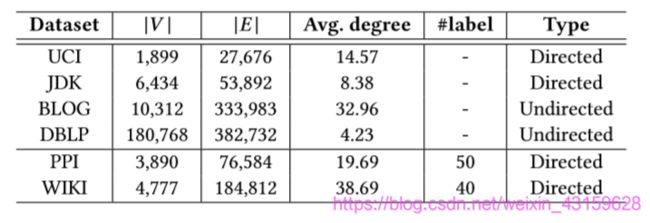
■(min@ϕ)∑_(1≤i 其中f_ϕ (x)ϵRd是给定输入x。L(·)是输入之间的损失函数。φij是x((i))与x^((j))之间的权重。 我们考虑的拉普拉斯特征映射(LE)可以很好地适应这个框架,LE可以通过网络结构来保留网络结构的属性。通常,可以通过最小化以下目标函数来获得嵌入, L_LE (ϕ;x)=∑_(1≤i 在本节中,我们介绍了NETRA,一种深度网络嵌入模型,使用了多个规范的自动编码器,能够平滑地将顶点序列作为输入进行正则化的顶点表示。结果表示可用于下游任务,例如,链接预测,网络重构和多类别分类。 在给定网络G(V,E)的情况下,利用DeepWalk[23]中的随机游动生成器,得到以每个顶点v∈V 在G(V,E)为根的截断随机游动(即序列化顶点)。 图解:在图2(a)中,深入探讨了它们对行走路径长度的影响。理由是,如果窗口设置为小于长度路径,那么它就会相当于增加样本的数量,从而减少行程长度。在图2(b)中,我们通过大幅度的方向减少了大小的变化[2]。 随机游走采样技术在网络嵌入研究中被广泛采用[12,23,37],但存在网络采样的稀疏性问题。对于给定网络中的每个顶点,如果假设平均节点度为d ̅,遍历长度为l,样本数为k,则可以计算遍历的采样率。 P_frac∝(|V|×K)/(|V|×d ̅^l )=k/d ̅^l ×100% (7) 采样分数的影响如图2所示。在本例中,DeepWalk用于在4.1节中描述的UCI消息网络上执行链接预测任务。从图2(a)和图2(b)可以看出,当遍历长度或平均顶点度增加时,性能显著下降1。根据Eq(7),很明显,当l或d ̅增加,游走的抽样比例越来越小。因此,由于输入稀疏,训练后的模型容易出现过拟合。相反,如果样本k的数量增加,性能会越来越好,如图2©所示。然而,更多的采样遍历也需要更多的模型训练的计算负担。因此,开发具有较强稀疏采样网络游动泛化能力的有效模型是十分必要的。 在本文中,我们提出了NETRA,它是一个具有对抗性规则的编码结构的模型,用于解决数据嵌入问题。自动编码器被广泛用于数据嵌入,例如图像和文档。它通过把输入数据映射到潜在空间来提供输入数据的信息量级的表示。正因为如此,如果编码器和解码器被允许过大的容量,那么复制任务就变成了学习任务,而没有提取出关于数据分布的有用信息[10]。我们建议使用弱的对抗性处理和互补性管理器。此外,生成性对抗训练提供了更鲁棒的离散空间表示,以了解稀疏采样步道上的过装配问题[19]。具体地说,在NETRA中,鉴别器通过比较来自自动编码器的潜在空间的样本和来自生成器的伪样本来更新,如图1所示。自编码器的潜在空间为网络中的顶点提供了最佳的嵌入,同时更新了编码器和鉴别器,由于LSTM考虑了采样步长的信息,因此本文使用LSTM作为编码器和解码器网络[27]。 这个联合体构造需要对每个部分进行培训。自动编码器可以通过最小化负的日志重建的可能性来解决这个问题,这可以通过实施的交叉点来实现。 L_AE (ϕ,ψ;x)=-Ε_(x~P_data (x) ) [dist(x,h_ψ (f_ϕ (x))], (8) 其中dist(x,y)=xlogy+(1-x)log(1-y)。这里x是来自训练数据的抽样批次。f_ϕ (x)是x的嵌入潜在表示,它也是鉴别器的正样本,在图1中用箭头表示“+”,φ和ψ分别是编码器和解码器功能的参数。在自动编码器的训练迭代中,不仅更新编码器和解码器,而且联合最小化保持位置损失(等式(6))。 如图1所示,NETRA最小化了来自编码器函数f_ϕ (x)~Ρ_ϕ (x)的学习表示与来自连续基因的表示之间的分布,和来自连续发生器模型的表示g_θ (z)~Ρ_θ (z)。Ρ_ϕ (x)和Ρ_θ (z)之间的地球移动距离的双重形式可以通过以下方式描述[1], W(Ρ_ϕ (x),Ρ_ϕ (z))=■(sup@||d(·)||(L≤1) )Ε(y~Ρ_ϕ (x)) [d(y)]-Ε_(y~Ρ_ϕ (z)) [d(y)] (9) 其中||d(·)||_(L≤1)是Lipschitz连续性约束(Lipschitz常数1)。如果我们有一个函数族{d_w (·)}w∈W对于某些K都是K-Lipschitz,那么我们有, W(Ρ_ϕ (x),Ρ_ϕ (z))∝■(max@wϵW) ■(Ε@x~P_data (x) )[d_w (f_ϕ (x))]-■(Ε@z~P_g (x) )[d_w (g_θ (z))] (10) 我们可以分离生成器和鉴别器。对于生成器,成本函数可以定义为, L_GEN (θ;x,z)=Ε_(X~Ρ_data (X) ) [d_w (f_ϕ (x))]-Ε_(Z~P_g (z) ) [d_w (g_θ (z))] (11) 而鉴别器的成本函数是, L_DIS (w;x,z)=-Ε_(X~Ρ_data (X) ) [d_w (f_ϕ (x))]+Ε_(Z~P_g (z) ) [d_w (g_θ (z))] (12) NETRA通过联合最小化自组织编码器重建错误和对抗训练过程中的局部保留损失来学习平滑表示。具体来说,我们考虑用目标函数求解联合优化问题, L_NETRA (ϕ,ψ,θ,w)=L_AE (ϕ,ψ,x)+λ_1 L_LE (ϕ,x)+λ_2 W(Ρ_ϕ (x),Ρ_θ (z)) (13) 定理3.1,设Ρ_ϕ (x)为任意分布。设Ρ_θ (z)为g_θ (z)的分布,其中z是从分布P_g (z)绘制的样本,而g_θ (·)是满足局部Lipschitz常数的函数E_(z~P_g (z) ) [L(θ,z)]<+∞。然后我们有: ∇_θ L_NETRA=-λ_2 ∇_θ Ε_(Z~P_g (Z) ) [d_w (g_θ (z))] (14) ∇_θ L_NETRA=-λ_2 ∇_w Ε_(X~P_data (X) ) [d_w (f_ϕ (x))]+λ_2 ∇_w Ε_(Z~P_g (z) ) [d_w (g_θ (z))] (15) ∇_ϕ L_NETRA=λ_1 ∇_ϕ ∑_(1≤i ∇_ψ L_NETRA=-∇_ψ Ε_(X~P_data (X) ) [dist(x,h_ψ (f_ϕ (x)))] (17) 证明 LetX⊆R^n是一个紧凑的集合,并且 V(d ̃,θ)=Ε_(y~Ρ_ϕ (x) ) [d ̃(y)]-Ε_(y~Ρ_θ (z) ) [d ̃(y)] 其中d ̃位于D = {d ̃:X→R,d ̃是连续的有界||d ̃||≤1}。由于X是紧致的,我们通过Kantorovich-Rubinstein二元性[1]知道存在一个d∈D获得价值 W(Ρ_ϕ (x),Ρ_θ (z))=■(sup@d ̃ϵD)V (d ̃,θ)=V (d ̃,θ) (19) 并且D^* (θ)={d∈D:V(d,θ)= W(Ρ_ϕ (x),Ρ_θ (z))}是非空的。根据包络定理[21],我们有: ∇_θ W(Ρ_ϕ (x),Ρ_θ (z))=∇_θ V(d,θ) (20) 对于任何d∈D^* (θ),我们可以得到: ∇_θ W(Ρ_ϕ (x),Ρ_θ (z))=∇_θ V(d,θ)=〖∇_θ Ε〗(y~Ρ_ϕ (x) ) [d(y)]-Ε(z~Ρ_g (z) ) [d(g_θ (z)] 因此,我们有∇_θ L_NETRA=-λ_2 ∇_θ Ε_(Z~P_g (Z) ) [d_w (g_θ (z))]。方程(15)-(17)是衍生定义的直接应用。 我们现在拥有所需的所有衍生物。为了训练模型,我们使用块坐标下降来优化模型的不同部分之间的交替:(1)局部保持损失和自动编码器重建误差(更新φ和ψ),(2)对抗训练过程中的鉴别器(更新w),和(3)生成器(更新θ)。算法1给出了完整方法的伪代码。 NETRA的训练过程包括以下步骤:首先,给定网络G(V,E),我们运行随机游走生成器获取长度l的随机游走。然后,将每个顶点的一个热表示x^((i))作为LSTM单元的输入。我们通过编码层传递随机遍历并获得顶点的矢量表示。在解码器网络之后,顶点表示将被转换回n维。通过最小化自动编码器操作中的重建误差,在输入和输出之间计算交叉熵损失。同时,保持局部性的约束确保相邻顶点非常接近(算法1中的步骤2-7)。编码器的潜在表示和发生器的输出将被反馈到鉴别器以获得对抗性损失(步骤10-17)。另外,通过穿过多层感知器,发生器将高斯噪声转换成与真实数据一样接近的潜在空间(步骤20-23)。在NETRA训练之后,我们通过将输入遍历编码器函数来获得网络的顶点表示f_ϕ (x)。 Algorithm 1 NetRA Model Training 最优性分析。如图1所示,NETRA可以解释为最小化两个分布之间的偏差,即P_ϕ (x)和P_θ (z)。我们提供以下命题,表明在我们的参数设置下,如果Wasserstein距离收敛,则编码器分布f_ϕ (x)~P_ϕ (x)收敛于发生器分布g_θ (z)~P_θ (z)。 命题3.2,令P为紧致集合X上的分布,并且(P_n)∈N分布为X。考虑到W(P_n,P)→0为n→∞,以下陈述是等价的: (1)P_n P 其中 表示随机变量的分布的收敛性。 (2)E_(x~P_n ) [F(x)]→E_(x~P) [F(x)],其中F(x)=∏_(i=1)n▒〖x_ipi,x∈Rn,∑_(i=1)n▒〖pi=k〗,k>1,k∈N〗。 证明(1)如[36]所示,P_n收敛到P等于W(P_n,P)→0。 (2)根据Portmanteau定理[36],Ε_(X~P_n ) [F(x)]→Ε_(X~P) [F(x)]得到F:Rn→R是有效的连续函数。我们的编码器f_ϕ (·)在整个球体上的输入正常化,并且通过tanh函数,生成器(θ)也是(-1,1)n。因此,对于所有Pi > 0,F(x)=∏_(i=1)n▒X_iPi 是有效的连续函数。 Ε_(X~P_n ) [∏_(i=1)n▒X_i(p^i ) ]→ Ε_(X~P) [∏_(i=1)n▒X_iPi ] (22) 表1:现实世界网络数据集的统计数据 计算分析。给定网络G(V,E),其中|V| = n,|E| = m,根据方程(6)中的定义,拉普拉斯算子特征图嵌入的总体复杂度为O(n)。在我们的实现中,我们只考虑在它们之间有边缘的顶点对(x((i)),x((j))),因此采样对的大小是O(m),这比O(n^2)小得多,因为真实网络在实际环境中很稀疏。 学习LSTM自动编码器的计算复杂度与参数数|φ|成比例和|ψ|在每次迭代中。因此,LSTM自动编码器的学习计算复杂度为O(n_epoch×(|φ| + |ψ|))。类似地,对于生成器和鉴别器,反向传播的每次调用通常在参数O(|θ|)和O(|w|)的数量上是线性的。因此,生成器和鉴别器的计算复杂度是O(n_epoch×(n_D×|w| + |θ|))。如果输入和隐藏层的大小大致相同,则它基本上是二次的。但是,如果我们将嵌入层的大小设置为远小于输入的大小,则时间复杂度会降低到O(n)。 利用网络数据集,从网络重构、链接预测、多标签分类等多方面对模型进行了性能评价。 为了验证所提出的网络嵌入模型的性能,我们在表1中对不同领域的网络进行实验,包括社会网络、软件依赖网络、生物网络和语言网络。 UCI消息(UCI)[22]是一个直接的通信网络,包含来自加利福尼亚大学的学生的在线社区的用户(顶点)之间的句子消息(边)。 JDK依赖(JDK)2是JDK 1.6.0.7框架的软件类依赖关系网络。网络是定向的,顶点表示Java类,两个顶点之间的边界表示重新存在两个类之间的依赖关系。 Blogcatalog (BLOG)[29]是一个来自BLOG Catalog网站的非定向社交网络,用于管理博客和他们的博客。顶点代表用户,边代表用户之间的友谊。 DBLP3是来自DBLP计算机科学参考书目的非直接合作作者。这个网络中的顶点代表作者,而边代表作者之间的生态权威。 Wikipedia (WIKI)[12]是一个有方向的单词网络。顶点标签表示使用Stanford POS- tagger[33]推断出的词性(POS)标签。 蛋白-蛋白相互作用(PPI)[3]是同系猿人PP网络的子图,是描述人类蛋白质之间相互作用的网络图。顶点标签表示蛋白质的生物学状态。 为了评价我们的网络嵌入模型的性能,本文总结以下几个竞争者。 谱聚类(SC)[30]:SC是一种基于矩阵分解的方法,用图的最小特征向量生成顶点表示。 DeepWalk[23]:基于DeepWalk的skip-gram[20]的模型,它学习了与垂直行走有关的知识。 node2vec[12]:这种方法结合了广度优先遍历深度优先遍历算法的优点。本文提出了结构等价的概念。 结构深层网络嵌入(SDNE)[37]:SDNE是一种基于深度分析的网络嵌入模型,它使用保持局部性的约束来学习捕捉高度非线性网络结构的顶点表示。 对抗网络嵌入(ANE)[6]:AN用于训练鉴别器以推动嵌入分布以匹配固定的先验值。 为了进行公平比较[18],除非另有说明,否则我们采用一种算法,在不同的数据集上生成300维顶点表示。将DeepWalk和node2vec中每个顶点的遍历次数设置为10,遍历长度为30,称为NETRA的随机遍历生成步骤,将DeepWalk和node2vec的窗口大小优化为10。对node2vec的回归和输入输出参数(p,q)∈{0.25,0.50,1,2,4}采用网格搜索进行优化。自动编码网络的定时器.将多层感知器(MLP)用于产生器和鉴别器.对算法进行评估,并将其应用于下行任务,如滑动预测,网络重构,以及后续的多标记分类。 为了演示网络嵌入模型如何很好地捕捉网络结构的关键特性,我们用特征比较法可视化了嵌入。使用t-SNE[35]的二维空间。图3给出了三个类:org.omg的红点,org.w3c的绿点,java.beans的蓝点。其他基线可以检测到不同程度的类。NETRA性能最佳,因为它能够将多个类别与多个边界分开,但两个策略之间只有很小的重叠。 链路预测任务的目的是在给定边缘去除一定比例的情况下推断出缺失的边,从网络中随机去除50%的边作为正样本,选择它们之间具有某种联系的顶点对作为负样本。通过网络嵌入算法学习顶点表示,得到顶点向量2范数的边缘特征,并直接利用其拓扑重新划分边缘,由于焦点在嵌入模型中,因此本文建立了基于假设的性能评价模型。连接顶点应该接近于欧氏空间。我们对链接预测任务进行AUC评分重估。结果如表2所示。显然,我们发现NETRA在所有数据集上的性能都大大优于基线算法。可以看出,基于四个数据集上的AUC评分,NETRA实现了3%到32%的改进。通过比较NETRA、node2vec和DeepWalk三种常用算法,可以看出生成对抗规则化在改进NETRA模型的泛化性能方面的有效性,在相同的随机游走序列下,NETRA能够克服取样序列的不足。 我们还绘制了这四个数据集的ROC曲线,如图4(a)-(d)所示。NETRA的ROC曲线主要接近于(0,1)点。结果如图4(e)-(h)所示。一般来说,在第一个纪元之后,我们可以观察到NETRA收敛速度快于AUC评分。与DeepWalk、node2vec、SDNE和ANE相比,NETRA收敛速度快于AUC评分。 网络嵌入是对原始网络的有效表示。通过网络嵌入学习到的顶点表示保持了网络重构的边缘信息。我们随机选择顶点对,在两者之间选择并计算欧几里德距离。我们使用精确度precision@k,前k预测中正确预测的分数,预估在 precision@k=1/k×|E_pred (1:k)⋂E_obs |, (23) 其中E_pred (1:k)表示原始网络中的pk预测和E_obs表示原始网络。在评估中,UCI消息和BlogCatalog数据集用于说明NETRA的性能,结果如图5所示。 根据精度@k曲线,NETRA模型在网络重构任务中实现了较高的精度。NETRA给出的重建结果非常精确地预测了大多数阳性样本(JDK和DBLP数据集上的结果没有包括在内)。利用生成性对抗性约束过程[11]、我们的模型将保持局部性和全局重构约束集成起来以获得捕获“语义”信息的嵌入。 最近对性能评估的研究中,网络嵌入算法学习到的顶点标记的预测任务很多[12,23,37]。有效的网络嵌入算法应该捕捉到下游机器学习任务最有用的特征。本文利用线[9]包对分类器进行回归,得到分类器的一个顶点特征与重逻辑回归。对于维基百科和PPI数据集,我们随机抽取10%到50%的顶点标记作为测试集,并使用它们作为测试集。我们的报告以Micro-F1[37]作为评估指标。每个结果平均五次运行,如图6所示。 从图中可以看出,NETRA优于多标记分类任务中的现有算法。在PPI数据集中,NETRA通过超过10%的未实验设置获得了比基线模型更高的micro-F1分数。在维基百科数据集中,NETRA模型在更低的百分比训练集下表现得更好。这说明在稀疏的环境下具有自我概括的性能。多标签分类器。由于LSTM自编码器具有通用性,因此其邻域信息可以被维数表示所捕获。 在本章中,我们研究了用于链路预测的NETRA的参数敏感性,研究了训练规模、嵌入维数和局部保持约束参数λ_1如何影响链路预测的性能。注意,对多标签分类和网络重构任务进行类似的观察扫描。 在图7(a)中,我们测量了UCI消息网络中的百分比。据我所知,性能随着训练量的增加而增加。与算法相比,NETRA可以捕获到两个边缘不均匀的边缘,这显示了涅特拉模型。在图7(b)中,我们将嵌入维数从50变化到1000,预测性能达到饱和,维数增加。考虑到嵌入维数与NETRA的参数体积有关,在模型化过程中存在性能与效率之间的矛盾。 参数λ_1由局部保持约束和自编码约束之间的相对强度定义。λ_1越高,来自局部类型保留约束的梯度越大。从图8中可以看出,较高的λ_1提高了UCI消息网络的预测性能,表明了重要的作用。 本文用NETRA的多个变异体来证明NETRA中个体成分的重要性,包括〖NETRA_〗LE、〖NETRA〗LSTM和〖NETRA〗GAN。〖NETRA〗LE和〖NETRA〗GAN移除局部保持约束LLE和对抗正则化W(P_ϕ (x),P_θ (z))。对于〖NETRA〗LSTM,我们用多层感知器代替LSTM。从图9中可以明显看出,LSTM自动编码器、局部保持约束和对抗正则化在NETRA模型中起着重要作用。在〖NETRA〗LSTM和〖NETRA〗_GAN的训练中,过度拟合变得明显。 最近,在自然语言处理成功的启发下,我们目睹了基于随机游走的方法[8,12,23]的出现[23]。它建立了网络结构和自然语言之间的联系。skip-gram算法[20]使随机游动中某一窗口内顶点间的共现概率最大。DeepWalk[23]利用截断随机游动得到了有效的嵌入。Node2vec[12]扩展了模型在同亲性和结构等价性之间的灵活性[42]。 深层学习模型[4,32,37]已经应用于解决嵌入问题。利用其学习高度非线性特性的能力,提出了基于自编码器的方法[4,37]。通过仔细构造学习目标,[37]保持了网络的第一和第二邻近性,从而提供了最先进的性能指标。最近关于图卷积网络[7,17]的研究已经对网络数据进行了有效的分层卷积运算。归纳的和无监督的图[14]利用顶点特征[15]并在顶点特征域之间聚集特征。 近几十年来,深层学习研究的迅速发展为高度非线性的心电研究提供了新方法。生成对抗网络(GAN)[11]实现了对高维数据的再现和学习表示[24]。使用GANs来研究两种代表性的学习。使用GANs来学习诸如自然语言和社交网络等离散性内容在通过离散随机变量进行反向传播时仍然存在问题。最近关于GAN的工作,如GraphGAN[38]和ANE[6]。尽管采用了离散结构[5,40]和改进的双编码器[16]。 在本研究中,我们提出了NETRA,它是一个嵌入模型的深层网络,它具有低维向量表示,并且具有通用的均一化结构。该模型不需要对隐式表示进行显式的先验密度分布,具有较好的泛化能力。特别地,利用LSTM自编码器,通过局部保持约束和生成对抗训练过程对顶点的采样序列进行正则化,从而获得对从网络中采样的稀疏顶点序列具有鲁棒性的光滑顶点表示。从本质上讲,我们评估了网络数据在不同任务中的表现,如网络重构、链接预测和多标签分类。 NIH U01HG008488、NIH R01GM115833、NIH U54GM114833、NSF IIS-1313606等为该工作提供支持。第四作者的研究是由陆军研究实验室赞助的,是在W911NF-09-2-0053号合作协议下完成的。这些观点和结论不应该被解释为代表陆军研究实验室或美国政府的官方政策。美国政府被授权为政府复制和分发转载件,尽管有任何版权。我们感谢匿名审稿人仔细阅读和深入评论手稿。 Martin Arjovsky, Soumith Chintala, and Léon Bottou. 2017. Wasserstein generative adversarial networks. In ICML. 214–223. Peter Borg and Kurt Fenech. 2017. Reducing the maximum degree of a graph by deleting vertices. Australasian Journal Of Combinatorics 69, 1 (2017), 29–40. Bobby-Joe Breitkreutz, Chris Stark, Teresa Reguly, et al. 2007. The BioGRID interaction database: 2008 update. Nucleic acids research 36, suppl_1 (2007), D637–D640. Shaosheng Cao, Wei Lu, and Qiongkai Xu. 2016. Deep Neural Networks for Learning Graph Representations… In AAAI. 1145–1152. Tong Che, Yanran Li, Ruixiang Zhang, R Devon Hjelm, Wenjie Li, Yangqiu Song, and Yoshua Bengio. 2017. Maximum-likelihood augmented discrete generative Quanyu Dai, Qiang Li, Jian Tang, and Dan Wang. 2017. Adversarial Network Embedding. arXiv preprint arXiv:1711.07838 (2017). Michaël Defferrard, Xavier Bresson, and Pierre Vandergheynst. 2016. Convolutional neural networks on graphs with fast localized spectral filtering. In NIPS. 3844–3852. Yuxiao Dong, Nitesh V Chawla, and Ananthram Swami. 2017. metapath2vec: Scalable representation learning for heterogeneous networks. In KDD. ACM, 135–144. Rong-En Fan, Kai-Wei Chang, Cho-Jui Hsieh, Xiang-Rui Wang, and Chih-Jen Lin.2008 LINEAR: A library for large linear classification. JMLR 9, Aug (2008), 1871–1874. Ian Goodfellow, Yoshua Bengio, Aaron Courville, and Yoshua Bengio. 2016. Deep learning. Vol. 1. MIT press Cambridge. Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. 2014. Generative adversarial nets. In NIPS. 2672–2680. Aditya Grover and Jure Leskovec. 2016. node2vec: Scalable feature learning for networks. In KDD. ACM, 855–864. Ishaan Gulrajani, Faruk Ahmed, Martin Arjovsky, Vincent Dumoulin, and Aaron Courville. 2017. Improved training of wasserstein gans. arXiv preprint arXiv:1704.00028 (2017). William L Hamilton, Rex Ying, and Jure Leskovec. 2017. Inductive Representation Learning on Large Graphs. arXiv preprint arXiv:1706.02216 (2017). Yoon Kim, Kelly Zhang, Alexander M Rush, Yann LeCun, et al. 2017. Adversarially Regularized Autoencoders for Generating Discrete Structures. arXiv preprint arXiv:1706.04223 (2017). Thomas N Kipf and Max Welling. 2016. Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907 (2016). Omer Levy, Yoav Goldberg, and Ido Dagan. 2015. Improving distributional similarity with lessons learned from word embeddings. Transactions of the Association for Computational Linguistics 3 (2015), 211–225. Alireza Makhzani, Jonathon Shlens, Navdeep Jaitly, and Ian Goodfellow. 2016. Adversarial Autoencoders. In ICLR. Tomas Mikolov, Ilya Sutskever, Kai Chen, Greg S Corrado, and Jeff Dean. 2013. Distributed representations of words and phrases and their compositionality. In NIPS. 3111–3119. Paul Milgrom and Ilya Segal. 2002. Envelope theorems for arbitrary choice sets. Econometrica 70, 2 (2002), 583–601. Tore Opsahl and Pietro Panzarasa. 2009. Clustering in weighted networks. Social networks (2009), 155–163. Bryan Perozzi, Rami Al-Rfou, and Steven Skiena. 2014. Deepwalk: Online learning of social representations. In KDD. ACM, 701–710. Alec Radford, Luke Metz, and Soumith Chintala. 2015. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv preprint arXiv:1511.06434 (2015). Sai Rajeswar, Sandeep Subramanian, Francis Dutil, Christopher Pal, and Aaron Courville. 2017. Adversarial Generation of Natural Language. arXiv preprint arXiv:1705.10929 (2017). Leonardo F.R. Ribeiro, Pedro H.P. Saverese, and Daniel R. Figueiredo. 2017. Ilya Sutskever, Oriol Vinyals, and Quoc V Le. 2014. Sequence to sequence learning with neural networks. In NIPS. 3104–3112. Jian Tang, Meng Qu, Mingzhe Wang, Ming Zhang, Jun Yan, and Qiaozhu Mei. 2015. Line: Large-scale information network embedding. WWW, 1067–1077. Lei Tang and Huan Liu. 2009. Relational learning via latent social dimensions. In KDD. ACM, 817–826. Lei Tang and Huan Liu. 2011. Leveraging social media networks for classification.Data Mining and Knowledge Discovery 23, 3 (2011), 447–478. Athanasios Theocharidis, Stjin Van Dongen, Anton J Enright, and Tom C Freeman.2008 Network visualization and analysis of gene expression data using BioLayoutExpress3D. Nature protocols 4, 10 (2009), 1535–1550. Fei Tian, Bin Gao, Qing Cui, Enhong Chen, and Tie-Yan Liu. 2014. Learning Deep Representations for Graph Clustering… In AAAI. 1293–1299. Tomasz Tylenda, Ralitsa Angelova, and Srikanta Bedathur. 2009. Towards timeaware link prediction in evolving social networks. In Proceedings of the 3rd workshop on social network mining and analysis. ACM, 9. Cédric Villani. 2008. Optimal transport: old and new. Vol. 338. Springer Science & Business Media. Daixin Wang, Peng Cui, and Wenwu Zhu. 2016. Structural deep network embedding. In KDD. ACM, 1225–1234. Hongwei Wang, Jia Wang, Jialin Wang, Miao Zhao, Weinan Zhang, Fuzheng Zhang, Xing Xie, and Minyi Guo. 2018. GraphGAN: Graph Representation Learning with Generative Adversarial Nets. AAAI (2018). J. Weston, F. Ratle, and R. Collobert. 2008. Deep learning via semi-supervised embedding. In ICML. Lantao Yu, Weinan Zhang, Jun Wang, and Yong Yu. 2017. SeqGAN: Sequence Generative Adversarial Nets with Policy Gradient. In AAAI. 2852–2858. Wenchao Yu, Guangxiang Zeng, Ping Luo, Fuzhen Zhuang, Qing He, and Zhongzhi Shi. 2013. Embedding with autoencoder regularization. In ECMLPKDD. Springer, 208–223. Daokun Zhang, Jie Yin, Xingquan Zhu, and Chengqi Zhang. 2016. Homophily, Structure, and Content Augmented Network Representation Learning. In ICDM. IEEE, 609–618. 网络分析在挖掘有用信息方面具有巨大的潜力,这些有用信息对诸如链接预测、社区检测和社会网络异常检测、生物网络和语言网络、语言网络等下游任务有利。在分析数据时,超顶点的低维向量表示(即网络结构被应用到向量空间),主要有两个挑战:1、复杂结构性质的保持;2、网络抽样的稀疏性。为解决以上的问题与挑战,现有的方法大多是从输入网络开始的遍历,然后建立具有最优允许维顶点嵌入顺序的模型。但是容易出现三个问题:1、稀疏样本产生一个复杂的模型而造成过拟合;2、固定的先验分布导致模型崩溃;3、未考虑先验分布而导致不能很好考虑邻近信息。 在本文的研究中,研究者提出了一个新的模型—NETRA,它用逆规则描述子(NETRA)来表示,NETRA联合地将局部保持最小化,并把自编码器的构造误差与短期记忆法(LSTM)结合起来。该模型在给定的网络G(V,E)中通过随机游走生成器获得长度为l的随机游走,将其中的每个顶点作为以编码器f_ϕ (·)(本文根据需求选用的是LSTM自动编码器)以及解码器h_ψ (·)训练出的自联想神经网络的输入,然后利用生成器g_θ (·)与鉴别器d_w (·)的极大极小值游戏生成对抗网络(GANs),之后通过网络嵌入方法通过给定的输入f_ϕ (x)ϵR^d以及输入之间的损失函数L(·)和权重φij学习关于网络结构信息的表示并逐渐优化。 NETRA模型构建工作完成后,研究者通过现有的一些数据集(UCImessage、Blogcatalog、DBLP3、Wikipedia)的测试以及与其他人的算法(谱聚类(SC)、DeepWalk、结构深层网络嵌入(SDNE)、node2vec、对抗网络嵌入(ANE))的网络重构、多标签分类、精度、性能、参数敏感性等方面的表现得对比,得出本文研究者提出的模型更好。 总的来说,本文的研究者们利用生成对抗训练过程,通过联合最小化局部保持损失和全局重构误差,提出了一种具有通用规则零树编码NETRA的深度网络嵌入模型。从网络上看,NETRA学会了从离散输入中产生有用的顶点表示,而不需要定义间接隐含空间先验知识。我们利用真实世界信息网络进行了网络重构、链接预测和多标记分类的广泛实验。并且通过同一模型不同数据集和同一测试集不同算法的实验结果表明NETRA的有效性和高效性。 3 途径
3.1 随机生成器

图2:网络采样的稀疏性 3.2 反向正则化自动编码器的嵌入
=Ε_(y~Ρ_ϕ (x) ) [d ̃(y)]-Ε_(z~Ρ_g (z) ) [d ̃(g_θ (z)] (18)
=〖-∇_θ Ε〗_(z~Ρ_g (z) ) [d_w (g_θ (z)] (21)
Require: the walks generated from input graph, maximum training epoch n_epoch, the number of discriminator training per generator iteration n_D.
1: for epoch = 0;epoch < n_epoch do
2: Minimizing L_LE(ϕ; x) with autoencoder L_AE (ϕ, ψ; x)
3: Sample {z^((i) ) } ■(B@i=1)~P_data (x) a batch from the walks
4: Compute latent representation f_ϕ (x^((i)))
5: Compute reconstruction output h_ψ (f_ϕ (x^((i))))
6: Compute〖 L〗_AE (ϕ, ψ) and L_LE (ϕ) using Eq.(8) and Eq.(6)
7: Backpropagate loss and update ϕ and ψ using Eq.(16)-(17)
8:
9: Discriminator training
10: for n = 0, n < n_D do
11: Sample {z^((i) ) } ■(B@i=1)~P_data (x) a batch from the walks
12: Sample {z^((i) ) } ■(B@i=1)~P_g (z) a batch from the noise
13: Compute representations f_ϕ (x^((i))) and g_θ (z^((i)) )
14: Compute L_DIS (w) using Eq.(12)
15: Backpropagate loss and update w using Eq.(15)
16: clip the weight w within [−c, c]
17: end for
18:
19: Generator training
20: Sample {z^((i) ) } ■(B@i=1)~P_g (z) a batch from the noise
21: Compute the representation g_θ (z^((i)) )
22: Compute 〖 L〗_GEN (θ) using Eq.(11)
23: Backpropagate loss and update θ using Eq.(14)
24: end for
4 评估
4.1 数据集
4.2 比较算法
4.3 可视化
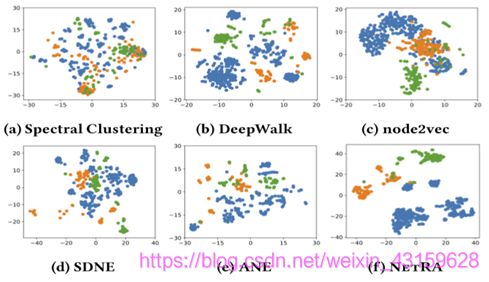
图3:JDK依赖关系网络上比较方法的可视化结果:红点属于org.omg类,绿点属于org.w3c类,蓝点属于java.beans类。 4.4 链路预测

图4:使用顶点表示的链接预测。用AUC ROC分数和训练时间进行评估。 4.5 网络重构
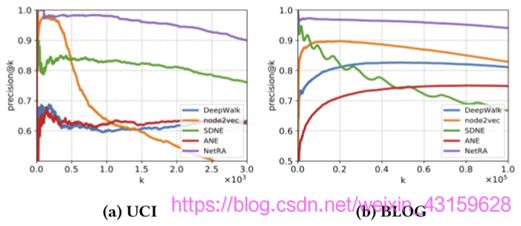
图5:UCI消息和博客目录的网络重构结果,通过precision@k进行评估。 4.6 多标记分类
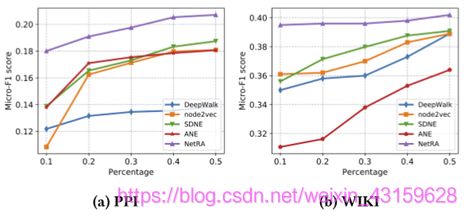
图6:PPI和维基百科的多标签分类
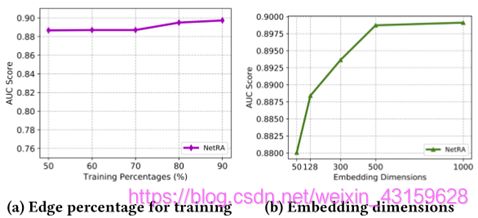
图7:参数敏感性分析
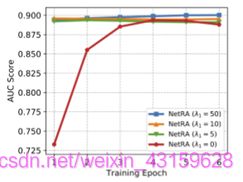
图8:LLE在不同λ_1上的性能
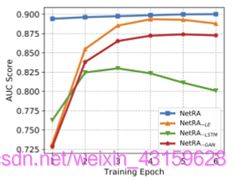
图9:不同NETRA架构的性能 4.7 参数敏感性
5 相关工作
6 结论
鸣谢
参考文献
adversarial networks. arXiv preprint arXiv:1702.07983 (2017).
Xiao Huang, Jundong Li, and Xia Hu. 2017. Label informed attributed network embedding. In WSDM. ACM, 731–739.
Struc2Vec: Learning Node Representations from Structural Identity. In KDD. ACM, 385–394.
Kristina Toutanova, Dan Klein, Christopher D Manning, and Yoram Singer. 2003. Feature-rich part-of-speech tagging with a cyclic dependency network. Association for Computational Linguistics, 173–180.
Laurens van der Maaten and Geoffrey Hinton. 2008. Visualizing Data using t-SNE. JMLR 9 (2008), 2579–2605.
总结与体会