论文阅读+实战：SimGNN：A Neural Network Approach to Fast Graph Similarity Computation

Part 1: 论文阅读

论文链接：SimGNN: A Neural Network Approachto Fast Graph Similarity Computation

1. 摘要

图相似性搜索是最重要的基于图的应用程序之一，例如查找与查询化合物最相似的化合物。图相似度/距离计算，例如图编辑距离（GED）和最大公共子图（MCS），是图相似度搜索和许多其他应用程序的核心操作，但在实践中计算成本很高。

作者受最近神经网络方法在几种图应用（例如节点或图分类）中取得成功的启发，提出了一种基于神经网络的新方法来解决这个经典但具有挑战性的图问题，旨在减轻计算负担的同时保持良好的性能。

2. 论文提出背景

• 图相似性搜索是最重要的基于图的应用之一
• 图编辑距离（GED）和最大公共子图（MCS），是图相似度搜索的核心操作，但在实践中计算成本很高
• 有两大类方法来解决图相似性搜索问题。第一类是剪枝验证框架；第二类试图直接降低图相似度计算的成本，以快速和启发式的方式找到近似值。第一类方法通过一系列数据库索引技术和剪枝策略，计算总量减少到易于处理的程度，但是指数时间复杂度的基本问题仍然存在。第二类方法通常需要基于离散优化或组合搜索的复杂设计和实现，时间复杂度通常仍然是多项式甚至是次指数的（相对于图中节点数）。

3. 前期工作

3.1 图编辑距离

形式上，G1 和 G2 之间的编辑距离，用GED(G1, G2) 表示，是在将 G1 转换为 G2 的最佳对齐中的编辑操作的数量，对图 G 的编辑操作是指插入或删除（顶点/边）和重新标记顶点。直观地说，如果两个图同构，则它们的 GED 为 0。下图显示了两个简单图之间的 GED 示例：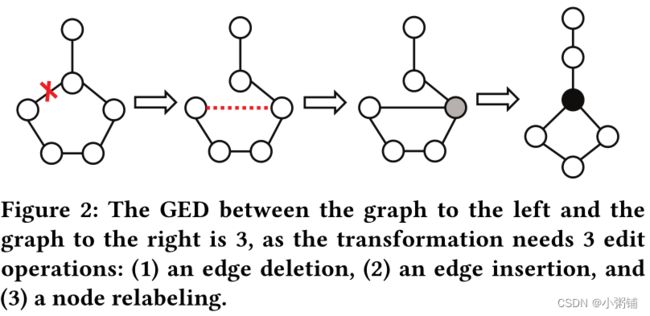

图1：图编辑距离 一旦计算了两个图之间的距离，我们就可以将其转换为介于 0 和 1 之间的相似度分数。

3.2 图卷积网络（GCN）

SimGNN 中的两种策略都需要计算节点嵌入。在策略 1 中，为了计算图级嵌入，它使用注意力聚合节点级嵌入；在策略 2 中，两个图的成对节点比较也是基于节点级嵌入计算的。
在许多现有的节点嵌入算法中，我们选择使用图卷积网络（GCN），因为它是图表示不变的，只要仔细设计初始化即可。它也是归纳的，因为对于任何看不见的图，我们总是可以在 GCN 操作之后计算节点嵌入。
GCN 现在是最流行的节点嵌入模型之一，属于基于邻居聚合的方法。它的核心操作，图卷积，对一个节点的表示进行操作，记为$u_n\in R^D$，定义如下：
$$conv(u_n)=f_1(\sum _{m\in N(n)}\frac{1}{\sqrt{d_n{d}_m}}{u}_m{W}_1^{(l)}+b_1^{(l)})$$

其中，$N(n)$是节点n的一阶邻域加上节点自身，$d_n$是节点度数加一，$W_1^{(l)}\in R^{D^l\times D^{l+1}}$是和GCN第l层卷积相关的权重矩阵，$b_1^{(l)}\in D^{l+1}$是偏移，$f_1(\cdot )$是类似于ReLU = max(0,x)的激活函数，直观地说，图卷积操作聚合了节点一阶邻居的特征和节点自身的特征。

4. SimGNN模型

该论文提出了一种加速图相似度计算的新方法，其目的与前面提到的第二类方法相同，但不是直接使用组合搜索计算近似相似度，而是将其变成一个学习问题。更具体地说，我们设计了一个基于神经网络的函数，将一对图映射到一个相似度分数。在训练阶段，该函数所涉及的参数将通过最小化预测的相似度得分与真实相似性得分之间的差异来学习，每个训练数据点都是一对图以及它们的真实相似度得分。在测试阶段，通过向学习函数提供任意一对图，我们可以获得预测的相似度分数。我们将这种方法命名为 SimGNN，即SIMilarity Computation via Graph Neural Networks.

4.1 前提条件

由于神经网络计算的性质，SimGNN 的关键优势在于效率高。然而，为了SimGNN模型的有效性，我们需要仔细设计神经网络架构以满足以下三个属性：

• (1) Representation-invariant. 通过排列节点的顺序，可以用不同的邻接矩阵表示同一个图。计算出的相似度分数应该不受这些变化的影响。
• (2) Inductive. 相似度计算应该推广到看不见的图，即计算训练图对之外的图的相似度分数。
• (3) Learnable. 该模型应该通过训练调整其参数来适应任何相似性度量

4.2 模型总体架构

概括地说，SimGNN是一种基于端到端神经网络的方法，它试图学习一个函数来将一对图映射到一个相似度分数。 SimGNN 的概述如下图所示：

图2：SimGNN架构 首先，我们的模型将每个图的节点转换为向量，对每个节点周围的特征和结构属性进行编码。然后，提出了两种策略来模拟两个图之间的相似性，一种基于两个图级嵌入之间的交互，另一种基于比较两组节点级嵌入。最后，将两种策略组合在一起，输入一个全连接的神经网络，得到最终的相似度分数。

4.3 模型策略

4.3.1 策略一：图级嵌入交互

该策略基于这样一个假设，即一个好的图级嵌入可以对图的结构和特征信息进行编码，并且通过交互两个图级嵌入，可以预测两个图之间的相似性。

它涉及以下阶段：

1. 节点嵌入阶段，将图的每个节点转换为向量，对其特征和结构属性进行编码；
2. 图嵌入阶段，通过基于注意力的聚合前一阶段生成的节点嵌入，为每个图生成一个嵌入；
3. 图-图交互阶段，接收两个图级嵌入并返回表示图-图相似度的交互分数；
4. 最终的图相似度得分计算阶段，进一步将交互得分降低为一个最终的相似度得分。它将与图对之间真实的相似度得分进行比较，以更新4个阶段所涉及的参数。

• Stage 1：节点嵌入
  我们采用 GCN，一种基于邻居聚合的方法，因为它学习了一个表示不变的聚合函数，并且可以应用于看不见的节点。
  原始节点表示是 one-hot 编码的（基于节点类型的，而非节点ID），对于具有未标记节点的图，我们将每个节点都视为具有相同的标签，从而产生与初始化表示相同的常数，然后将节点特征和邻接矩阵输入多层 GCN生成节点嵌入。
• Stage 2：图嵌入：全局上下文感知注意力
  我们提出了以下注意机制，让模型学习由特定相似度指标引导的权重。我们将输入节点嵌入表示为 $U\in R^{N\times D}$。首先，计算全局图上下文 $c\in R^D$，它是施以非线性变换的节点嵌入的简单平均值： $c=tanh((\frac{1}{N}{\sum }_{n=1}^N{u}_n)W_2)$，其中 $W_2\in R^{D\times D}$ 是可学习的权重矩阵。上下文 c 通过学习权重矩阵提供了适应给定相似度度量的图的全局结构和特征信息。基于 c，我们可以为每个节点计算一个注意力权重。
  对于节点 n，为了使其注意力了解全局上下文，我们取 c 与其节点嵌入之间的内积。直觉是，类似于全局上下文的节点应该接收更高的注意力权重。将 sigmoid 函数 $f_2(x)=\frac{1}{1+exp(-x)}$应用于结果，以确保注意力权重在 (0, 1) 范围内。我们没有将权重归一化为长度 1，因为希望嵌入范数反映图的大小，这对于图相似度计算的任务是必不可少的。
  最后，图嵌入$h\in R^D$是节点嵌入的加权和$h={\sum }_{n=1}^N{a}_n{u}_n$。总的节点注意机制总结如下：
  $$h=\sum _{n=1}^N{f}_2(u_n^{T}c)u_n=\sum _{n=1}^N{f}_2(u_n^{T}tanh((\frac{1}{N}\sum _{m=1}^N{W}_2))u_n$$
• Stage 3：图-图交互：神经张量网络
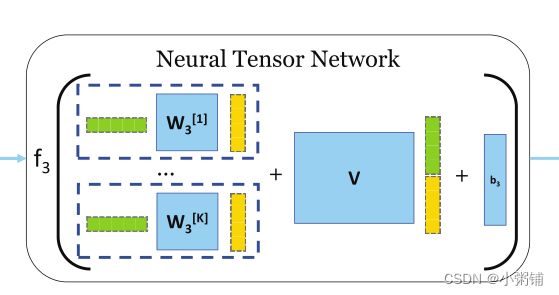
  针对前一阶段生成的两个图的图级嵌入，对它们的关系进行建模的一种简单方法是取两者的内积。然而，这种方式会导致两者之间的交互不足。因此，我们使用神经张量网络 (NTN) 来模拟两个图级嵌入之间的关系：
  $$g(h_i,h_j)=f_3(h_i^T{W}_3^{[1:K]}{h}_j+V[\begin{array}{c}{h}_i\\ h_j\end{array}]+b_3)$$
  其中，$h_i\in R^D,h_j\in R^D$是注意力层生成的图嵌入对，$W_3^{[1:K]}\in R^{D\times D\times K}$是权重张量，[]表示连接操作，$V\in R^{K\times 2D}$是权重向量，$b_3\in R^K$是偏移向量，$f(\cdot )$是激活函数，K 是一个超参数，控制模型为每个图嵌入对产生的**交互（相似性）分数的数量。**神经张量网络示意图如下：
  

图3：神经张量网络

• Stage 4：图相似度得分计算在获得相似度得分列表后，我们应用标准的多层全连接神经网络逐步降低相似度得分向量的维数。最后，预测一个分数 $\widehat{s_{ij}}\in \mathbb{R}$，并使用以下均方误差损失函数将其与真实相似性分数进行比较：
  $$\mathcal{L}=\frac{1}{|\mathcal{D}|}\sum _{(i,j)\in \mathcal{D}}(\widehat{s_{ij}}-s({\mathcal{G}}_i,{\mathcal{G}}_j))$$
  其中，$\mathcal{D}$是训练图对的集合，$s({\mathcal{G}}_i,{\mathcal{G}}_j)$是${\mathcal{G}}_i,{\mathcal{G}}_j$之间的基准相似性。
• 策略一的局限性
  图级嵌入可能会丢失节点级信息，例如节点特征分布和图大小。在许多情况下，两个图之间的差异在于较小的子结构，很难通过图级嵌入来反映。一个类比是，在自然语言处理中，基于每个句子一个嵌入的模型的句子匹配的性能可以通过使用细粒度的词级信息进一步增强，这导致了我们的第二个策略。

4.3.2 策略二：成对节点比较

为了克服前面提到的限制，我们考虑绕过 NTN 模块，直接使用节点级嵌入。如图三底部数据流所示，如果 ${\mathcal{G}}_i$ 有 $N_i$个节点，${\mathcal{G}}_j$ 有 $N_j$ 节点，则会有$N_i{N}_j$成对交互分数，由$S=\sigma (U_i{U}_j^T)$ 获得，其中$U_i\in R^{N_i\times D}$ 和 $U_j\in R^{N_j\times D}$ 分别是 ${\mathcal{G}}_i$ 和 ${\mathcal{G}}_j$ 的节点嵌入。由于节点级嵌入没有被归一化，因此应用sigmoid 函数来确保相似度得分在 (0, 1) 的范围内。对于两个不同大小的图，为了强调它们的大小差异，我们将假节点填充到较小的图中。如图 3 所示，将两个具有零嵌入的假节点填充到底部图，从而在 S 中产生两个额外的零列。
表示 $N=max(N_1,N_2)$。成对节点相似度矩阵 $S\in R^{N\times N}$ 是一个有用的信息来源，因为它编码了细粒度的成对节点相似度分数。利用 S 的一种简单方法是将其向量化：$vec(S)\in R^{N^2}$，并将其馈送到全连接层。但是，图节点之间通常没有自然排序。同一图的不同初始节点排序将导致不同的$S$和$vec(S)$。
为了确保模型图表示不变性，可以通过应用一些节点排序方案对图进行预处理，但我们考虑了一种更有效和更自然的方式来利用 S。我们提取其 直方图特征 : $hist(S)\in {\mathbb{R}}^B$，其中 B 是控制直方图中 bin 数量的超参数。在图 3 的情况下，直方图使用了七个 bin。直方图特征向量被归一化并与图级交互分数 $g(h_i,h_j)$ 连接，并馈送到全连接层以获得图对的最终相似度分数。
不懂什么是直方图特征
需要注意的是，仅直方图特征不足以训练模型，因为直方图不是连续微分函数，不支持反向传播。事实上，我们依靠策略 1 作为更新模型权重的主要策略，并使用策略 2 来补充图级特征，这为我们的模型带来了额外的性能提升。
综上所述，我们结合了策略 1 捕获的粗略全局比较信息和策略 2 捕获的细粒度节点级比较信息，以提供图与模型比较的全面视图。

4.3.3 时间复杂度分析

一旦 SimGNN 被训练，它就可以用来计算任何一对图的相似度得分。时间复杂度涉及两部分：

1. 节点级和全局级嵌入计算阶段，每个图需要计算一次；
   • 时间复杂度为 O(E)，其中 E 是图的边数。
   • 注意，图级嵌入可以预先计算和存储，并且在图相似度搜索的设置中，未见过的查询图只需处理一次即可获得其图级嵌入。
2. 相似度计算阶段，需要对每对图进行计算
   • 策略 1 的时间复杂度为 $O(D^{2}K)$，其中 D 是图级嵌入的维度，K 是 NTN 的特征图维度。我们的策略 2 的时间复杂度是 $O(D{N}^2)$，其中 N 是较大图中的节点数。这可以通过节点采样来构建相似矩阵 S 来减少策略2的复杂度。此外，矩阵乘法 $S=\sigma (U_1{U}_2^T)$ 可以通过 GPU 大大加速。我们在实验中验证了使用第二种策略时没有明显的运行时间增加。

总之，在我们提出的两种策略中： 策略 1 是主要策略，它是有效的，但仅基于粗略的图级嵌入；策略二是辅助性的，包含细粒度的节点级信息，但比较耗时。在最坏的情况下，该模型在关于节点数量的二次时间中运行，这是用于近似图距离计算的最先进算法之一。

5. 实验

5.1 数据集

实验使用了三个真实世界的图形数据集。

• 第一个数据集是AIDS，它是NCI/NIH开发治疗计划中的抗病毒筛选化合物的集合，已用于几个现有的图形相似性搜索工作。它含有42687种化合物结构，其中省略了氢原子。我们选择700个图，每个图都有10个或少于10个节点。每个节点都标有29种类型中的一种，如图4a所示：
  

图4(a)：AIDS数据集的节点标签分布

• 第三个数据集是LINUX。它由48747个从Linux内核生成的程序依赖关系图（PDG）组成。每个图表示一个函数，其中节点表示一条语句，边表示两条语句之间的依赖关系。我们随机选择1000个图，每个图的节点数等于或小于10个。节点未标记。
• 第三个数据集是IMDB。IMDB数据集由1500个电影演员的自我网络组成，如果这两个人出现在同一部电影中，就有边相连。为了测试我们提出的方法的可伸缩性和效率，我们使用了完整的数据集。节点未标记。
• 三个数据集的统计数据如表1、图4（b）、图4（c）所示
  
  

图4(b)：三个数据集的图大小分布 图4(c): 三个数据集的图编辑距离分布

5.2 数据预处理

对于每个数据集，我们将所有图的 60%、20% 和 20% 分别随机拆分为训练集、验证集和测试集。评估反映了图查询的真实场景：对于测试集中的每个图，我们将其视为一个查询图，并让模型计算查询图与数据库中每个图的相似度。数据库图根据计算的与查询的相似性进行排名。
由于来自 AIDS 和 LINUX 的图相对较小，因此使用名为 A* 的指数时间精确 GED 计算算法来计算所有图对之间的 GED。然而，对于 IMDB 这样的大数据集，A* 不能再使用，因为“ 目前没有可用的算法能够在超过 16 个节点的图之间的合理时间内可靠地计算 GED” 。
为了正确处理 IMDB 数据集，我们采用三种著名的近似算法计算的最小距离，Beam 、Hungarian 和 VJ 。然后取最小值而不是平均值，因为它们返回的 GED 保证大于或等于真实 GED。
为了将基准真相GEDs转换为基准真相相似度分数来训练我们的模型，我们首先根据Qureshi等人提出的方法[33] 对GEDs进行归一化：$nGED({\mathcal{G}}_1,{\mathcal{G}}_2)=\frac{GED({\mathcal{G}}_1,{\mathcal{G}}_2)}{(|{\mathcal{G}}_1|+|{\mathcal{G}}_2|)/2}$，其中${\mathcal{G}}_i$表示${\mathcal{G}}_i$节点的数量，然后我们采用指数函数 $\lambda (x)=e^{-x}$ 将归一化的 GED 转换为 (0, 1] 范围内的相似度得分。注意 GED 和相似度之间存在一对一的映射关系分数。

5.3 基线方法

我们的基线包括两种类型的方法，快速近似 GED 计算算法和基于神经网络的模型。
第一类基线包括三种经典的 GED 计算算法。

• (1) A*-Beamsearch（光束）[28]。它是次指数时间的 A* 算法的变体
• (2) Hungarian[23,35]
• (3) VJ分别是基于匈牙利算法的二分图匹配[9] 和 Volgenant 和 Jonker 算法[18] 的两种三次时间算法。

第二类基线包括以下神经网络架构的七个模型。

• (1) SimpleMean 简单地采用图的所有节点嵌入的未加权平均值来生成其图级嵌入
• (2) HierarchicalMean (分层平均）
• (3) HierarchicalMax [7] 是基于图粗化的原始 GCN 架构，它们使用全局均值或最大池化来生成图层次结构。我们使用来自 GCN 5 第一作者的 Github 存储库的实现。接下来的四个模型将注意力机制应用于节点。
• (4) AttDegree 使用节点度数的自然对数作为其注意力权重
• (5) AttGlobalContext
• (6) AttLearnableGlobalContext (AttLearnableGC) 都利用全局图上下文来计算注意力权重，但前者没有对上下文应用具有可学习权重的非线性变换，而后者则使用了
• (7) SimGNN 是我们的完整模型，它结合了策略 1 (AttLearnableGC) 和策略 2 的优点

5.4 参数设置

对于模型架构，我们将 GCN 层数设置为 3，并使用 ReLU 作为激活函数。对于初始节点表示，我们针对有节点标记的 AIDS 采用反映节点类型的 one-hot 编码方案，对于没有节点标记的 LINUX 和 IMDB 采用常量编码方案。 GCN 的第 1 层、第 2 层和第 3 层的输出维度分别为 64、32 和 16。
对于 NTN 层，我们将 K 设置为 16。对于成对节点比较策略，我们将直方图 bin 的数量设置为 16。我们使用 4 个全连接层来降低NTN 模块的串联结果，从 32 到 16、16 到 8、8 到 4 和 4 到 1。
我们在一台配备 Intel i7-6800K CPU 和一个 Nvidia Titan GPU 的机器上进行所有实验。至于训练，我们将批量大小设置为 128，使用 Adam 算法 [21]进行优化，并将初始学习率固定为 0.001。我们将迭代次数设置为 10000，并根据最低验证损失选择最佳模型。

5.5 评价指标

我们采用以下指标用于评估所有模型：

• 时间。收集每个模型计算一对图的相似度得分所需的时间。
• 均方误差 (MSE)。均方误差测量计算的相似度和真实相似度之间的均方差。
  我们还采用以下指标来评估排名结果。
• Spearman 秩相关系数 (ρ) [39] 和 Kendall 秩相关系数 (τ) [20] 衡量预测的排名结果与真实排名结果的匹配程度。
• k (p@k) 处的精度。p@k 是通过将预测的前 k 个结果与真实的前 k 个结果的交集除以 k 来计算的。与 p@k 相比，ρ 和 τ 评估全局排名结果，而不是关注前 k 个结果。

5.6 结果

1. 有效性
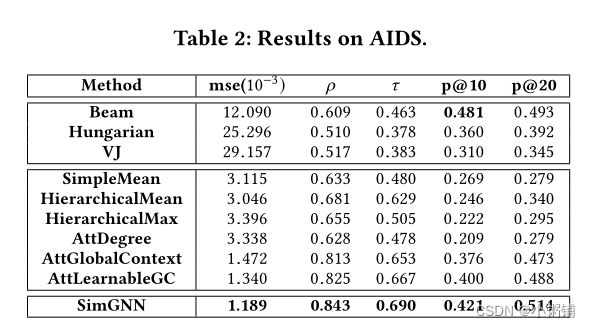
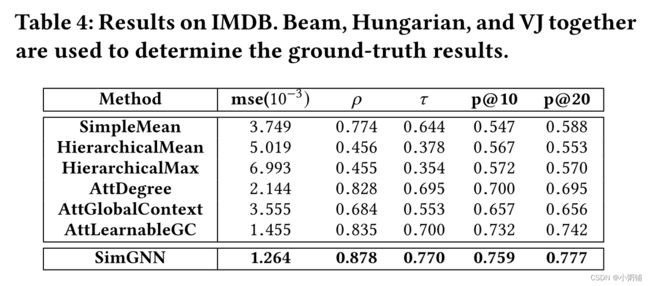
   由表 2、3 和 4 中可知，我们的模型在三个数据集均有效，三个数据集的所有指标上始终达到最佳或次佳性能。在基于神经网络的方法中，SimGNN 在所有指标上始终取得最佳结果。这表明我们的模型可以学习一个很好的嵌入函数，该函数可以推广到看不见的测试图。
   
   
   
   值得注意的是，在基于神经网络的模型中，AttDegree 在 IMDB 上取得了较好的效果，但在 AIDS 或 LINUX 上却没有。这可能是由于 IMDB 中普遍存在的独特的自我网络结构。如图 10 所示，高度中心节点表示特定的演员/女演员（他/她自己），关注哪个可能是合理的启发式。相比之下，AttLearnableGC 通过可学习的全局上下文适应 GED 指标，并且始终比 AttDegree 表现更好。结合策略 2，SimGNN 实现了更好的性能。
   
   节点注意力的可视化可以在图 5 中看到。我们观察到以下类型的节点接收相对较高的注意力权重：
   • 度数较大的中心节点，例如(a) 和 (b) 中的“S”，带有标签的节点很少出现在数据集中，例如（f）中的“Ni”，（g）中的“Pd”，（h）中的“Br”
   • 形成特殊子结构的节点，例如（e）中的两个中间“C”等。
     这些模式具有直观意义，进一步证实了所提出方法的有效性。
     
2. 效率
   三个数据集的效率比较如图 6 所示。基于神经网络的模型在所有三个数据集上始终取得最佳结果。具体来说，与精确算法 A* 相比，SimGNN 在 AIDS 上快 2174 倍，在 LINUX 上快 212 倍。 A* 算法甚至不能应用于大型图，并且在 IMDB 的情况下，它的变体 Beam 仍然比 SimGNN 慢 46 倍。
   
   SimGNN测量的时间包括图嵌入的时间。如果预先计算和存储图嵌入，SimGNN 将花费更少的时间。所有这些都表明，在实践中，使用 SimGNN 作为图相似度计算的快速方法是合理的，这对于大型图尤其如此，因为在 IMDB 中，与 AIDS 和 LINUX 相比，我们的计算时间并没有增加太多。

5.7 参数灵敏度

我们评估了图级嵌入的维度和直方图箱的数量如何影响结果。我们报告艾滋病的均方误差。如图 7a 所示，如果使用更大的尺寸，性能会变得更好。这很直观，因为更大的嵌入维度使模型有更多的能力来表示图。在我们的策略 2 中，如图 7b 所示，性能对直方图箱的数量相对不敏感。这表明在实践中，只要直方图的 bin 不是太少，就可以获得相对较好的性能。

5.8 实例探究

我们在图 8、9 和 10 中演示了三个示例查询，一个来自每个数据集。在每个演示中，第一行描述了查询以及真实排名结果，并标有查询的标准化 GED；底行显示了我们的模型返回的图表，每个图表的排名都显示在顶部。


上述结果表明，SimGNN有能力检索类似于查询的图形，例如对于 LINUX（图 9），前 6 个结果是查询的同构图。

6. 相关工作

6.1 网络/图嵌入

节点级别嵌入：年来，提出了几种用于学习节点表示的方法，包括基于矩阵分解的方法（NetMF[32]）、基于skip-gram的方法（DeepWalk[31]、Node2Vec[12]、LINE[40]）、自动编码器的方法（SDNE[43]）、邻域聚合的方法（GCN[7、22]、GraphSAGE[13]）等。
图形级别嵌入：为每个图生成一个嵌入的最直观的方法是通过简单的平均值或一些加权平均值来聚合节点级嵌入，称为“基于总和”的方法[14]。通过将图形视为分层数据结构并应用图形粗化，可以实现更复杂的图形表示方法[7，47]。此外，[19]通过直方图聚合节点集，[29]在图上应用节点排序以使其适合CNN。
图上的注意力机制：使用注意力引导行走来查找与图形分类最相关的部分。因此，它只从整个图中选择了固定数量的节点，这对于我们的任务（图相似性计算）来说太粗糙了。[41，42]为节点级任务的每个节点邻居分配注意权重。我们是第一批将注意力机制应用于图形相似性计算任务的人。
图神经网络应用：基于神经网络的方法已经处理了大量基于图形的应用程序，其中大多数是作为节点级别的预测任务[27，37]。然而，一旦转移到图级任务，大多数现有的工作都涉及单个图的分类[7，29，47]。在这项工作中，我们首次考虑了图的相似性计算。

6.2 图的相似性计算

图距离/相似性度量：图形编辑距离（GED）[3]可以视为字符串编辑距离度量[25]的扩展，它定义为通过序列图形编辑操作将一个图形转换为另一个图形所需的最小成本。另一个度量是最大公共子图（MCS），它相当于某个成本函数下的GED[4]。图核[11,16,30,46]可以被视为一系列不同的图相似性度量，主要用于图分类。
成对GED计算算法：已经提出了一系列近似算法来降低时间复杂度，同时牺牲精度[2，6，9，28，35]。我们知道最近的一些工作声称它们的时间复杂度为O（n2）[2]，但它们的代码在这个阶段是不稳定的。
图形相似性搜索：计算GED是图形数据库分析中的一个基本算子，已被用于一系列关于图形相似性搜索的工作[26，44，48，49，51]。这些研究侧重于数据库级技术，以加快涉及精确GED计算的整个查询过程。

7.讨论与未来方向

未来的工作有几个方向：
（1）我们的模型可以处理具有节点类型的图形，但不能处理边缘特征。在化学中，化合物的键通常是标记的，因此将边缘标记合并到我们的模型中是有用的；
（2） 很有希望探索不同的技术来进一步提高topk结果的精度，这主要是由于训练数据集中的相似性分布偏斜而没有很好地保持；
（3）考虑到无法计算大型图的精确GED这一约束条件，学习只在小型图之间的精确GEDs上训练的模型如何推广到大型图。

参考文献

[7] Michaël Defferrard, Xavier Bresson, and Pierre Vandergheynst. 2016. Convolutional neural networks on graphs with fast localized spectral filtering. In NIPS.3844–3852.
[9] Stefan Fankhauser, Kaspar Riesen, and Horst Bunke. 2011. Speeding up graph edit
distance computation through fast bipartite matching. In International Workshop on Graph-Based Representations in Pattern Recognition. Springer, 102–111.
[18] Roy Jonker and Anton Volgenant. 1987. A shortest augmenting path algorithm for dense and sparse linear assignment problems. Computing 38, 4 (1987), 325–340.
[20] Maurice G Kendall. 1938. A new measure of rank correlation. Biometrika 30, 1/2
(1938), 81–93.
[21] Diederik P Kingma and Jimmy Ba. 2015. Adam: A method for stochastic optimization. ICLR (2015).
Harold W Kuhn. 1955. The Hungarian method for the assignment problem. Naval research logistics quarterly 2, 1-2 (1955), 83–97.
[28] Michel Neuhaus, Kaspar Riesen, and Horst Bunke. 2006. Fast suboptimal algorithms for the computation of graph edit distance. In Joint IAPR International Workshops on Statistical Techniques in Pattern Recognition (SPR) and Structural and Syntactic Pattern Recognition (SSPR). Springer, 163–172.
[33] Rashid Jalal Qureshi, Jean-Yves Ramel, and Hubert Cardot. 2007. Graph based
shapes representation and recognition. In International Workshop on Graph-Based
Representations in Pattern Recognition. Springer, 49–60.
[35] Kaspar Riesen and Horst Bunke. 2009. Approximate graph edit distance computation by means of bipartite graph matching. Image and Vision computing 27, 7(2009), 950–959.
[39] Charles Spearman. 1904. The proof and measurement of association between two things. The American journal of psychology 15, 1 (1904), 72–101.