Hopfield神经网络以及其python实现（一）

摘要

对于上世纪八十年代初神经网络的研究复兴而言，Hopfield起到了举足轻重的作用。在早期的学术活动中，Hopfield曾研究光和固体间的相互作用，而后，他集中研究生物分子间的电子转移机制，他在数学和物理学上的学术研究和他后来在生物学上的经验的结合，在当今被称为cross-disciplinary，为日后神经网络的研究以及概念的提出建立了坚实的基础。Hopfield神经网络于1982年被提出，可以解决一大类模式识别问题，还可以给出一类组合优化问题的近似解。这种神经网络模型后被称为Hopfield神经网络。1985年Hopfield在PRD发表的文章详细阐述了该网络与Ising Model的联系，并且提出了其相变特性。
本文主要从四个方面阐述作者在近些日子以来对Hopfield神经网络的了解与体会，主要以其Python实现为主，根据代码的优化以及结果的优化说明其主要应用以及可能的改进。并且阐明其与Ising Model的联系以及相变特性。由于最后一部分涉及大量热力学相关知识，本科知识略显羞涩，故主要提出作者的一些体会与朦胧的感受。

主要内容

• General Features.
• algorithm
• Python code implementation
• thermodynamic characteristics related to Ising Model.

一，网络特性

在之前的学习中，我们已经接触了非常多常见的神经网络。例如， 神经元的输出可以在下一个时间段直接作用到自身的RNN, 设计精巧并且得到最大程度应用的FNN, 由于图像中存在固有的局部模式（如人脸中的眼睛、鼻子、嘴巴等），所以将图像处理和神将网络结合引出卷积神经网络的CNN，为了克服梯度消失，ReLU、maxout等传输函数代替了sigmoid的DNN等。作为我们非常熟悉的神经网络，这些网络在工业和生活中已经非常成熟并且得到了广泛的应用。Hopfield神经网络是一种非常典型的反馈型神经网络，除了与前馈神经系统相同的神经元之间的前馈连接，很明显还存在一种反馈连接。总体上而言，Hopfield网络结构可以用以下示意图描述：

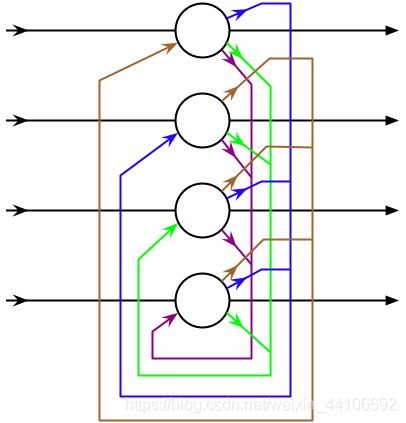
从示意图中可知，该神经网络结构具有以下三个特点：

• 神经元之间全连接，并且为单层神经网络。
• 每个神经元既是输入又是输出，导致得到的权重矩阵相对称，故可节约计算量。
• 在输入的激励下，其输出会产生不断的状态变化，这个反馈过程会一直反复进行。假如Hopfield神经网络是一个收敛的稳定网络，则这个反馈与迭代的计算过程所产生的变化越来越小，一旦达到了稳定的平衡状态，Hopfield网络就会输出一个稳定的恒值。
• Hopfield网络可以储存一组平衡点，使得当给定网络一组初始状态时，网络通过自行运行而最终收敛于这个设计的平衡点上。当然，根据热力学上，平衡状态分为stable state和metastable state, 这两种状态在网络的收敛过程中都是非常可能的。
• 为递归型网络，t时刻的状态与t-1时刻的输出状态有关。之后的神经元更新过程也采用的是异步更新法（Asynchronous)。

本文章主要探讨神经元状态为二值：+1，-1情况下的离散型网络。上文提到的稳定状态，具体含义为迭代如下的神经元输出，$\sigma {}_i^{\mu }=sgn({\sum }_j^{}J{}_{ij}\sigma {}_j^{\mu })$最终使得整个系统的神经元状态在迭代前后保持稳定。另外，值得一提的是，从数学上也可证明迭代到最后稳定的状态，该状态也是能量上的一个局部最小值（local minimum)。这里定义能量：$H=-{\sum }_{<i,j>}^{}J{}_{ij}\sigma {}_i^{\mu }\sigma {}_j^{\mu }$.这里的能量函数虽然形式上与物理上一致，但是代表的是系统的转化趋势。最终达到的稳定态可能是能量函数的亚稳态值。式中$\sigma {}_i^{\mu }$代表第$\mu$个pattern下的系统中第i个神经元的状态，在离散的情况下，有+1和-1两个状态。$J{}_{ij}$代表神经元之间的耦合系数，更常称为两个神经元之间的权重，可以表达为：$J{}_{ij}=\frac{1}{N}{\sum }_{\mu =1}^p\xi {}_i^{\mu }\xi {}_j^{\mu }$，其中$\mu$依然表示为pattern, 从1至p个，N代表神经元的数目，$\xi$代表神经元+1和-1的状态。由此，可以完全将H用$\sigma$和$\xi$等变量表示，从而表示出配分函数Z， 便可研究其热力学特性，这一些都是后话了。
可见，Hopfield神经网络是一种单层、全连接的递归型神经网络，并且可通过上文提到的迭代获得系统的某种稳定状态。这便是通过该网络获取回忆过程的总体原理。

二，详尽算法

首先，我们考虑用该网络存储一张二值图片，根据某个阈值色度可将每一张图片导出为0-1图片。假设我们图片的像素为n$\times$n（也可以用向量代表），我们需要使用一个含有n个节点的网络来存储这张图片。根据前文提到的权重，每两个神经元之间的权重矩阵定义为$J{}_{ij}=\frac{1}{N}{\sum }_{\mu =1}^p\xi {}_i^{\mu }\xi {}_j^{\mu }$。这里我们解释一下为什么权重矩阵是这样取的。前文我们也提到了能量函数$H=-{\sum }_{<i,j>}^{}J{}_{ij}\sigma {}_i^{\mu }\sigma {}_j^{\mu }$，形式与物理学热统中的能量函数如出一辙，事实上，能量函数的形式是可以任意定义的。这里这样定义可能是刻意与Ising Model靠近，以获得更多有用的信息，并且这个形式也刚好可以解释节点状态变化带来的整个系统的transforming trend. 读者可以任意取一些特殊点来验证这个观点。
Hopfield神经网络并不是只能存储一张图片的鸡肋存在，如果我们需要存储另外一张图片，我们可以也利用同样的方法，获得另外的权重矩阵，两个权重矩阵相加，就可以获得整个系统的记忆权重矩阵。看到这里，读者可能会问：生成一个矩阵，如何能回忆起多张图片？事实上，这里作者的理解是，每一个权重矩阵都有一个局部最小值，那么权重矩阵相加带来的结果就是许多个局部最小值，如下图所示：

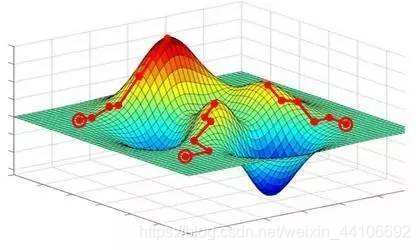
根据实验结果，该网络会自动筛选出和原图像最类似的test picture, 故猜测，在构造出来的能量空间内，若输入一个测试图像，即向量的位置靠近某一个局部极小值，在迭代的过程中掉入收敛到这个极小值，即为回忆起所谓的原始图像。当然，这个状态空间不是我们日常认为的三维空间，而是更类似固体物理中的k空间。
在利用输入的训练图片，根据之前的公式，获得权重矩阵，或者耦合系数矩阵之后（就像上文说的，一个矩阵包含了所有图片的信息），将该记忆矩阵保存。之后便到了更新神经元的步骤。为了得知神经网络的回忆特性，我们输入一个有扰动的图片，观察网络能否回忆起该图片扰动之前的样子。依然是将图片矩阵化，得到二值矩阵。这里我们采用异步更新法则（Asynchronous）：$\sigma {}_i^{\mu }=sgn({\sum }_j^{}J{}_{ij}\sigma {}_j^{\mu })$，根据激活函数获得+1与-1二值。异步更新法则也是更符合生物体的回忆特性，每次只更新一个神经元，每一个神经元更新都可以用到最新更新神经元的状态，从而可以减小计算内存，加快计算速度。迭代的结果，可能有三个：有限循环状态，混沌状态，稳定状态。若网络是不稳定的，由于DHNN网每个节点的状态只有1和-1两种情况，网络不可能出现无限发散的情况，而只可能出现限幅的自持振荡，这种网络称为有限环网络。
在有限环网络中，系统在确定的几个状态之间循环往复，系统也可能不稳定收敛于一个确定的状态，而是在无限多个状态之间变化，但是轨迹并不发散到无穷远，这种现象叫做混沌。为保证异步方式工作时网络收敛，权重矩阵应为对称阵，而这一点在程序中和前文的理论准备中已经有体现。
最后，测试图片迭代至稳态或者亚稳态，此时的状态即可认为网络已回忆起原始图片。

三，Python程序详解

首先，说明自己使用的库名、库类型与模块等，本代码所使用的主要如下：

import numpy as np
import random
from PIL import Image
import os
import re
import matplotlib.pyplot as plt
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"

之后，开始按照自己的习惯把算法分解成为可理解的若干分块。在这个过程中，发现有许多步骤需要将图片转换为二值矩阵或者其逆操作等，故先写几个函数便于调用。
下面这个函数用于将jpg格式或者jpeg格式的图片转换为二值矩阵。先生成x这个全零矩阵，从而将imgArray中的色度值分类，获得最终的二值矩阵。这个函数在全文中将多次调用。

def readImg2array(file,size, threshold= 145):
    #file is jpg or jpeg pictures
    #size is a 1*2 vector,eg (40,40)
    pilIN = Image.open(file).convert(mode="L")
    pilIN= pilIN.resize(size)
    #pilIN.thumbnail(size,Image.ANTIALIAS)
    imgArray = np.asarray(pilIN,dtype=np.uint8)
    x = np.zeros(imgArray.shape,dtype=np.float)
    x[imgArray > threshold] = 1
    x[x==0] = -1
    return x

下面在定义的便是其逆变换，由于Python中已经有该逆变换的函数，故只是稍作加工便可使用。

def array2img(data, outFile = None):

    #data is 1 or -1 matrix
    y = np.zeros(data.shape,dtype=np.uint8)
    y[data==1] = 255
    y[data==-1] = 0
    img = Image.fromarray(y,mode="L")
    if outFile is not None:
        img.save(outFile)
    return img

写到这一步，已经可以输入原始图片获得该二值矩阵了。这里需要注意，选取图片时尽量选取黑白分明的图片以获得好的display, 可以调整size与threshold改变最后图片的对比度以及图片大小。如下图便是一个输出：

下面是另一个为了方便计算而编写的程序，利用x.shape得到矩阵x的每一维个数，从而得到m个元素的全零向量。将x按i\j顺序赋值给向量tmp1. 最后得到从矩阵转换的向量。

def mat2vec(x):
    #x is a matrix
    m = x.shape[0]*x.shape[1]
    tmp1 = np.zeros(m)

    c = 0
    for i in range(x.shape[0]):
        for j in range(x.shape[1]):
            tmp1[c] = x[i,j]
            c +=1
    return tmp1

接下来便是非常重要的一步，创建$H{}_{ij}$,即权重矩阵，根据权重矩阵的定义$J{}_{ij}=\frac{1}{N}{\sum }_{\mu =1}^p\xi {}_i^{\mu }\xi {}_j^{\mu }$。根据权重矩阵的对称特性，可以很好地减少计算量。

#use Hebbian rule create weight matrix
def create_W_single_pattern(x):
    # x is a vector
    if len(x.shape) != 1:
        print ("The input is not vector")
        return
    else:
        w = np.zeros([len(x),len(x)])
        for i in range(len(x)):
            for j in range(i,len(x)):
                if i == j:
                    w[i,j] = 0
                else:
                    w[i,j] = x[i]*x[j]
                    w[j,i] = w[i,j]
    return w

下一个需要建立的函数便是输入test picture之后对神经元的随机升级。利用异步更新，以及前面提到的迭代公式，从而获取更新后的神经元向量以及系统能量。

#randomly update
def update_asynch(weight,vector,theta=0.5,times=100):
    energy_ = []
    times_ = []
    energy_.append(energy(weight,vector))
    times_.append(0)
    for i in range(times):
        length = len(vector)
        update_num = random.randint(0,length-1)
        next_time_value = np.dot(weight[update_num][:],vector) - theta
        if next_time_value>=0:
            vector[update_num] = 1
        if next_time_value<0:
            vector[update_num] = -1
        times_.append(i)
        energy_.append(energy(weight,vector))
    
    return (vector,times_,energy_)
                

为了更好地看到迭代对系统的影响，我们按照定义计算每一次迭代后的系统能量，最后画出E的图像，便可验证前文的观点。

def energy(weight,x,bias=0):
#weight: m*m weight matrix
#x: 1*m data vector
#bias: outer field
    energy = -x.dot(weight).dot(x.T)+sum(bias*x)
    # E is a scalar
    return energy

定义完主要的函数之后，我们来到main body部分，调用前文定义的函数，便可简洁地把主函数表达清楚。可以调整size和threshod获得更好的输入效果，但是也有可能会增大计算机的计算量而增加运行时间。为了增加泛化能力，我们正则化之后打开训练图片，并且通过该程序获取权重矩阵。

#main 
#import training picture
size_global =(80,80)
threshold_global = 60

train_paths = []
train_path = "/Users/lichan/Desktop/hopfield/train_pics/"
for i in os.listdir(train_path):
    if re.match(r'[0-9 a-z A-Z-_]*.jp[e]*g',i):
        train_paths.append(train_path+i)
flag = 0
for path in train_paths:
    matrix_train = readImg2array(path,size = size_global,threshold=threshold_global)
    vector_train = mat2vec(matrix_train)
    plt.imshow(array2img(matrix_train))
    plt.title("train picture"+str(flag+1))
    plt.show()
    if flag == 0:
        w_ = create_W_single_pattern(vector_train)
        flag = flag +1
    else:
        w_ = w_ +create_W_single_pattern(vector_train)
        flag = flag +1

w_ = w_/flag
print("weight matrix is prepared!!!!!")
    

得到权重矩阵之后的第一步自然是输入测试图片，依然正则化之后，根据图片-矩阵-图片的方式，将测试图片转换为二值图像如下图所示。

## import test data
test_paths = []
test_path = "/Users/lichan/Desktop/hopfield/test_pics/"
for i in os.listdir(test_path):
    if re.match(r'[0-9 a-z A-Z-_]*.jp[e]*g',i):
        test_paths.append(test_path+i)
num = 0
for path in test_paths:
    num = num+1
    matrix_test = readImg2array(path,size = size_global,threshold=threshold_global)
    vector_test = mat2vec(matrix_test)
    plt.subplot(221)
    plt.imshow(array2img(matrix_test))
    plt.title("test picture"+str(num))

最后一步，我们利用对测试图片的矩阵（神经元状态矩阵）进行更新迭代，直到满足我们定义的迭代次数。最后将迭代末尾的矩阵转换为二值图片输出。运用之前定义的函数，这一步可谓是一气呵成。

  #plt.show()
    oshape = matrix_test.shape
    aa = update_asynch(weight=w_,vector=vector_test,theta = 0.5 ,times=8000)
    vector_test_update = aa[0]
    matrix_test_update = vector_test_update.reshape(oshape)
    #matrix_test_update.shape
    #print(matrix_test_update)
    plt.subplot(222)
    plt.imshow(array2img(matrix_test_update))
    plt.title("recall"+str(num))

    #plt.show()
    plt.subplot(212)
    plt.plot(aa[1],aa[2])
    plt.ylabel("energy")
    plt.xlabel("update times")
    
    plt.show()

至此，实现Hopfiled的Python程序已经全部完成，我们来看一下在之前希拉里的输入图片下，训练-回忆之后，我们能得到什么样的输出？

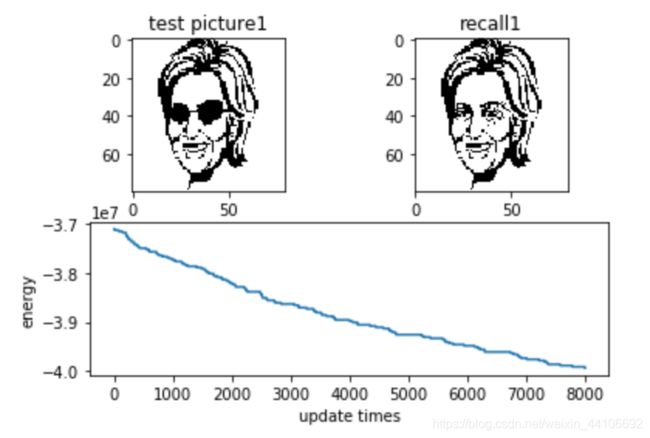
在输入测试图片，迭代8000次之后，程序可以较为精准地回忆起希拉里的原图片。并且可以看出，系统的能量符合随着迭代次数而减小的特点，逐渐进入稳态或者亚稳态。程序依然有许多不足，例如在照片精度较大的情况下运行的时间过长（主要是能量函数的计算）。
本篇文章中，作者主要介绍了离散型Hopfield神经网络的基本特点，算法以及实现Python程序，以及近期来的一些感想与体会。在下一篇文章中主要阐述其热力学特征，对于神经网络而言，用Ising Model的求解可以获取许多热力学特征，解释一些直觉现象，因此也是十分重要。敬请期待！

四，Reference

1. https://en.wikipedia.org/wiki/Hopfield_network
2. Daniel J Amit .Storing Infinite Numbers of Patterns in a Spin-Glass Model of Neural Networks[J].PRL,:,1985.55(14):1530-1533.
3. https://github.com/yosukekatada/Hopfield_network