数据挖掘——无监督学习

一、概述

无监督学习算法：让计算机自己学习，没有属性或者标签

有监督学习算法：每个样本都已经被标明，我们已经被告知了学习的答案

无监督学习的典型算法是聚类算法和降维

二、聚类算法

1、概念：聚类分析，将数据对象分组成为多个蔟，同一簇中的对象彼此相似，不同簇中的对象彼此相异

2、功能：作为一个独立的工具来获得数据分布的情况，作为其他算法（如特征和分类）的预处理的步骤

3、应用场景：帮市场分析人员从客户基本库中发现不同的客户群体，从而可以对不同的客户群采取不同的营销策略。保险业：发现汽车保险中索赔率较高的客户群；城市规划：根据房子的类型、价值和地理位置对其进行分组

4、评判标准：

可扩展性：大多数来自于机器学习和统计学领域的聚类算法在处理数百万条数据时能够体现出高效率来

处理不同数据类型的能力：数字型、二次元型、图像型等等

发现任意形状的能力：基于距离的聚类算法往往发现的是球形的聚类，其实现实的聚类是任意形状的

处理噪声数据的能力：对空缺值、离群点、数据噪声不敏感

对于输入数据的顺序不敏感：同一个数据集合，以不同的次序提交给同一个算法，应该产生相似的结果

5、主要的聚类方式：

基于划分的方法：将数据集中的对象分配到n个簇中，并且通过设定目标函数来驱使算法趋向于目标，且每个组至少包含一个对象，每个对象必须只属于一个组，如K-means聚类、K均值算法

基于层次的方法：是指对于给定的数据集对象，我们通过层次聚类算法获得一个具有层次结构的数据集合子集结合的过程，层次聚类分为两种：自底向上的凝聚法、自顶向下的分裂法

基于密度的方法：基于主要特点: 发现任意形状的聚类 处理噪音 需要密度参数作为终止条件、如DBSCAN 

（DBSCAN聚类方式 一个动态网站：    https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/）

三、DBSCAN

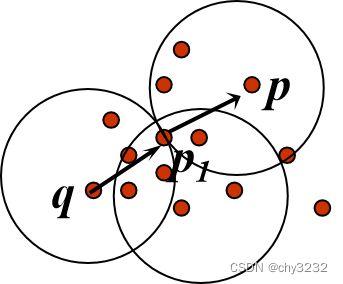
密度可达: 点 p 关于Eps, MinPts 是从 q密度可达的：如果 存在一个节点链 p1, …, pn, p1 = q, pn = p 使得 pi+1 是从pi直接密度可达的。（不是对称关系）

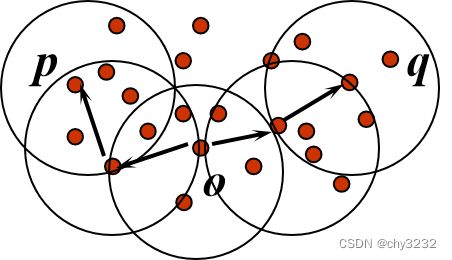
密度相连的: 点 p关于 Eps, MinPts 与点 q是密度相连的：如果 存在点 o 使得, p 和 q 都是关于Eps, MinPts 是从 o 密度可达的（是对称的）

 

利用密度相连的特性来发现连通的稠密区域 任意两个足够靠近(eps内)的核心点将放在一个簇内 任何与核心点足够靠近的边界点也会被放入与核心点的相同的簇 

 2、DBSCAN算法步骤

（1）检测数据库中尚未检查过的对象p，如果p未被处理(归为某个簇或者标记为噪声)，则检查其邻域，若包含的对象数>=minPts，建立新簇C，将其中的所有点加入候选集N；若<=minPts 则暂时标记为噪声

（2）对候选集N 中所有尚未被处理的对象q，检查其邻域，若至少包含minPts个对象，则将这些对象加入N；如果q 未归入任何一个簇，则将q 加入C；

（3）重复步骤2)，继续检查N 中未处理的对象，当前候选集N为空；

（4）重复步骤1)~3)，直到所有对象都归入了某个簇或标记为噪声。

四、降维

1、降维：减少要考虑的随机变量的数量 降维分析是指将高维数据到低维数数据空间（二维或三维）的变化过程，其目的是为了降低时间的复杂度和空间复杂度或者是去掉数据集中夹杂的噪音又或者是为了使用较少的特征进行解释，方便我们可以更好地解释数据以及实现数据的可视化 

2、降维的必要性

 

 

特征维度减少的方法：

实现维度减少有两种技术，既特征选择和特征提取：特征选择指的是选择原始数据集中最具代表性或者统计意义的维度特征；特征提取指的是将原始特征转换为一组具有明显物理意义或者统计意义的特征

 特征选择的代码实现：

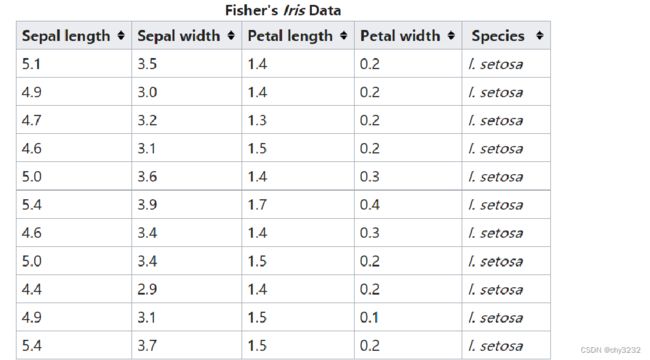
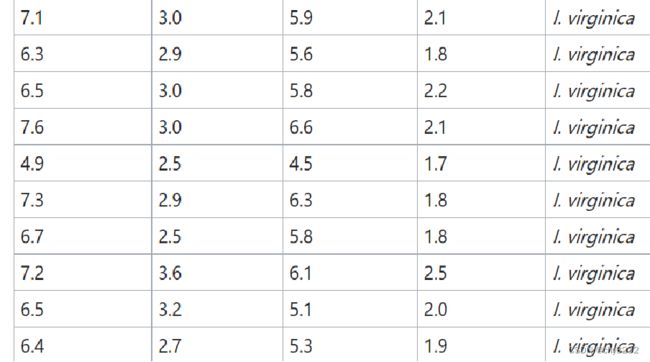
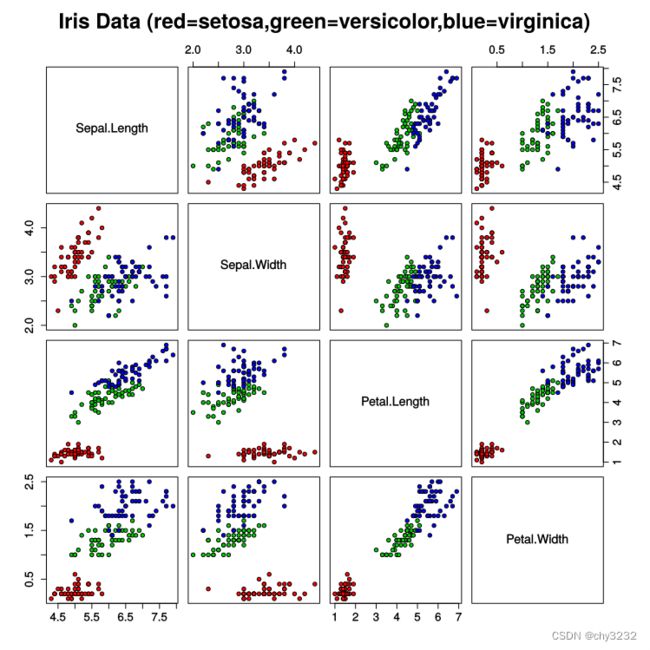
from sklearn.datasets import load_iris 
from sklearn.feature_selection import SelectKBest 
from sklearn.feature_selection import chi2
iris = load_iris() >>> X, y = iris.data, iris.target 
X_new = SelectKBest(chi2, k=2).fit_transform(X, y)

特征提取 ：

特征提取指的是将原始特征转换为一组具有明显物理意义或者统计意义的特征 提取指的是我们并不会因此丢弃某些维度的数据，而转换指的是保留所有的维度数据，只是将高维数据投影低维数空间

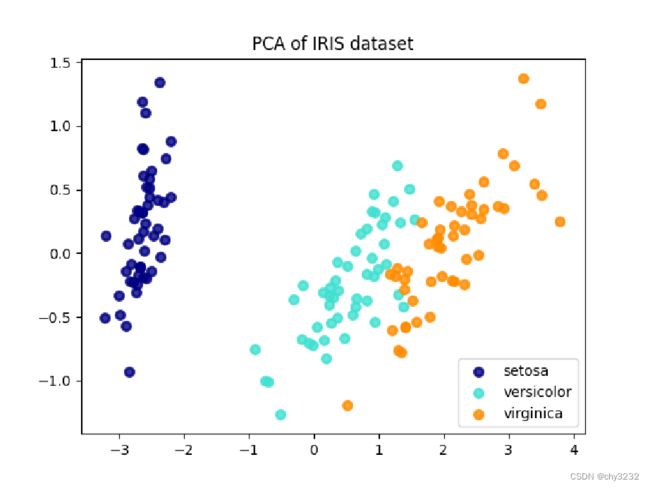
五、PCA算法

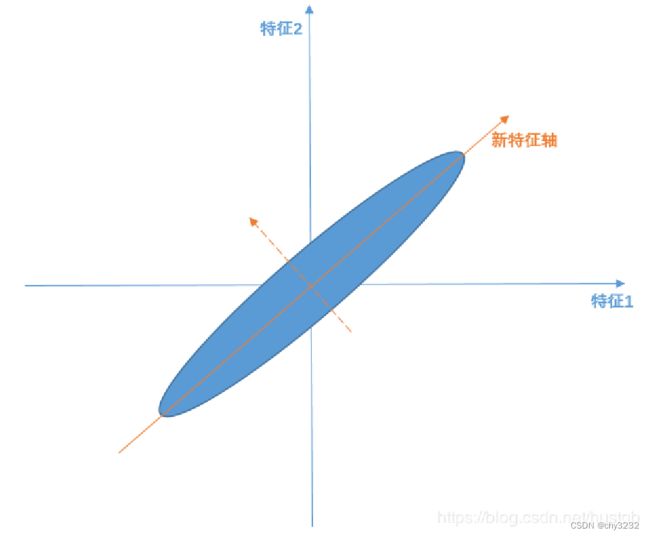
PCA图示

PCA算法过程

线性变换=>新特征轴可由原始特征轴线性变换表征 线性无关=>构建的特征轴是正交的 主要线性分量（或者说是主成分）=>方差最大的方向（希望投影后投影值尽可能分散，而这种分散程度，可以用数学上的方差来表述） PCA算法的求解就是找到主要线性分量及其表征方式的过程 

PCA代码的实现

from sklearn import datasets
iris = datasets.load_iris()
data=iris.data
from sklearn.decomposition import PCA 
pca=PCA(n_components=2)
newData=pca.fit_transform(data)