机器学习1一回归模型（一）

机器学习前先了解

数据挖掘常用的6个模块：

模块名称	模块作用	应用场景
math数学模块	科学计算方法，例如平方根、对数计算、三角函数等	对数据进行标准化、求统计值等处理
datetime日期时间模块	处理时间类型的数据，例如时间数据格式化、时间获取、时间数据与字符串的转换等	数据通常会带有时间戳，有时时间还是一种重要的特征
random随机模块	主要进行随机数的生成(随机选取)	进行数据采样、数据生成经常用到这些随机方法
file文件操作模块	提供文件操作，包括文件的读取和写入	数据挖掘的样本通常都会被存放文件中，所以文件操作也是基本技能之一
re正则匹配模块	使用正则表达式来进行字符串的匹配、检测等	处理文本数据时，经常需要用到正则匹配来进行文本的检索
sys系统接口模块	主要实现与操作系统交互的一些功能，例如获取当前操作系统的情况、设置编码格式等，编写完整的程序通常都会用到	系统接口模块主要是为了获取系统的各种数据

python的第三方库：

• 基础模块有：

名称	含义
Numpy	python语言扩展程序库，支持大量的维度数组和矩阵运算 。
Scipy	集成数学、科学和工程的计算包，有效于计算Numpy矩阵，方便Numpy和Scipy协同工作。
Matplotlib	专门用来绘制图的工具包，可以用它来进行数据分析。
pandas	数据分析工具包，它基于Numpy构建，纳入了大量的库和标准数据模型。

• 机器学习常用的库

名称	含义
scikit-learn	基于SciPy进行延伸的机器学习工具包，包含大量的机器学习算法模型，有6大基本功能:分类、回归、聚类、数据降维、模型选择和数据预处理。
OpenCV	非常庞大的图像处理库，实现了非常多的图像和视频处理方法，如图像视频加载、基础特征获取、边缘检测等，处理图像通常都需要其支持。
NLTK	比较传统的自然语言处理模块，自带很多语料，以及全面的传统自然语言处理算法。比如字符串处理、卡方检验等。
Gensim	包含了浅层词嵌入的文本处理模块，以及常用的自然语言处理相关方法，如 TF-IDF、 word2vec等模型。

---

前言

1.什么是回归

上图是一个简单的回归模型，X坐标是质量，Y坐标是用户满意度，从图中可知，产品的质量越高其用户评价越好，这可以拟合一条直线 y = ax + b 来预测新产品的用户满意度。

在回归模型中，我们需要预测的变量叫做因变量，比如产品质量；选取用来解释因变量变化的变量叫做自变量，比如用户满意度。回归的目的就是建立一个回归方程来预测目标值，整个回归的求解过程就是求这个回归方程的回归系数。

回归定义：

给出一个点集，构造一个函数来拟合这个点集，并且尽可能的让该点集与拟合函数间的误差最小，如果这个函数曲线是一条直线，那就被称为线性回归，如果曲线是一条三次曲线，就被称为三次多项回归。

2.什么是线性回归

线性：结果和特征之间是一次函数关系，比如上述例子中直线y = ax + b 。
非线性：结果和特征之间不是一次函数关系，比如二次函数、三次函数，在图中表示的是一条曲线
由于我们的数据不是完全分布在直线y = ax + b 上的，从而需要一个方法来评估每次产生的线的效果，然后去相应的调整来达到最好的效果。引入两个概念：
损失函数： 计算每个样本点的结果值和当前函数值的差值。具体使用的是 惨差平方和。
最小二乘法： 通过损失函数来计算假设结果为直线y = ax + b 的情况下，得出损失值的大小。而最小二乘法就是要找一组a、b的值，使得损失值达到最小。

• 例题
  
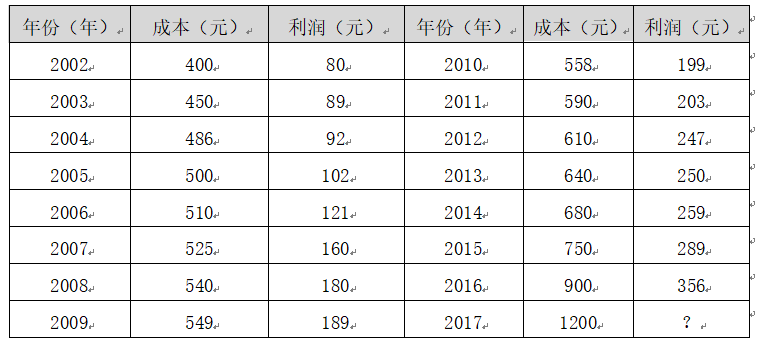
  假设存在表中的数据集，它是某产品的成本和利润数据集。数据集中2002年到2016年的数据集称为训练集，整个训练集共15个样本数据。重点是成本和利润两个变量，成本是输入变量或一个特征，利润是输出变量或目标变量，整个回归模型如下图所示。
  
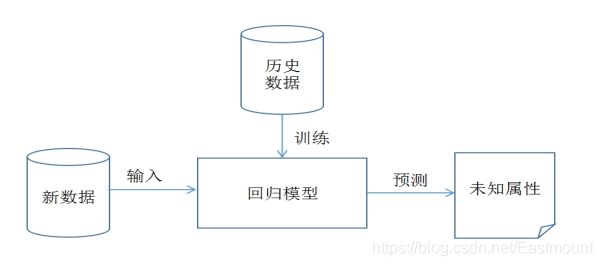
  建立模型，x表示产品成本，y表示产品利润，h表示将输入变量映射到输出变量y的函数，对应一个因变量的线性回归（单变量线性回归）公式如下：
  
  误差是指预测y值和真实y值之间的差值，使用误差的简单累加将使得正差值和负差值相互抵消，所采用的平方误差（最小二乘法）如下：
  
  线性回归模型的损耗函数如下：
  
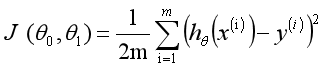
  选择适当的参数让其最小化min，即可实现拟合求解过程。通过上面的这个示例，我们就可以对线性回归模型进行如下定义：根据样本x和y的坐标，去预估函数h，寻求变量之间近似的函数关系。公式如下：
  
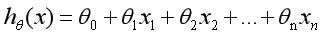
  其中，n表示特征数目，表示每个训练样本的第i个特种值，当只有一个因变量x时，称为一元线性回归；而当多个因变量时，成为多元线性回归。我们的目的是使最小化，从而最好的将样本数据集进行拟合，更好地预测新的数据。

---

一、线性回归 (Linear Regression)

线性回归算法思想主要是求解一组因变量和自变量之间的方程，得到回归函数，同时误差项通常使用最小二乘法进行计算。 机器学习Sklaern包中将调用Linear_model子类的LinearRegression类进行线性回归模型计算。

1.LinearRegression的使用

LinearRegression回归模型在Sklearn.linear_model子类下，主要是调用fit(x,y)函数来训练模型，其中x为数据的属性，y为所属类型。

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
参数说明：

copy_X：布尔型，默认为True。是否对X复制，如果选择False，则直接对原始数据进行覆盖，即经过中心化、标准化后，把新数据覆盖到原数据上。
fit_intercept：布尔型，默认为True。是否对训练数据进行中心化，如果是True表示对输入的训练数据进行中心化处理，如果是False则输入数据已经中心化处理，后面的过程不再进行中心化处理。
n_jobs：整型，默认为1。计算时设置的任务个数，如果设置为-1表示使用所有的CPU。
normalize：布尔型，默认为False。是否对数据进行标准化处理。

LinearRegression类主要包括如下方法：

方法	作用
fit(X,y[n jobs])	对训练集 x，y进行训练，分析模型参数，填充数据集。其中X为特征，y为标记或类属性
predict(X)	使用训练得到的估计器或模型对输入的X数据集进行预测，返回结果为预测值。数据集x通常划分为训练集和测试集。
decision function(X)	使用训练得到的估计器或模型对数据集X进行预测。它与predict(X)区别在于该方法包含了对输入数据的类型检查和当前对象是否存在coef_属性的检查，更安全。
score(X,y[,]samples weight)	返回对于以X为samples、y为target的预测效果评分。
get params([deep])	获取该估计器(Estimator)的参数。
set params( **params)	设置该估计器(Estimator)的参数。
coef_	存放 LinearRegression模型的回归系数。
intercept_	存放 LinearRegression模型的回归截距。

• 对上述的产品成本和利润数据集进行线性回归实验。

from sklearn import linear_model     #导入线性模型
import matplotlib.pyplot as plt       
import numpy as np

# 数据输入，X表示企业成本 Y表示企业利润
X = [[400], [450], [486], [500], [510], [525], [540], [549], [558], [590], [610], [640], [680], [750], [900]]
Y = [[80], [89], [92], [102], [121], [160], [180], [189], [199], [203], [247], [250], [259], [289], [356]]

# 回归训练
clf = linear_model.LinearRegression() 
clf.fit(X, Y) # 对训练集X，Y进行训练

#预测结果
X2 = [[400], [750], [950]]
Y2 = clf.predict(X2)
Y2
res = clf.predict(np.array([1200]).reshape(-1, 1)) # reshape(-1,1)表示（任意行，1列）
# reshape(行数，列数)常用来更改数据的行列数目
# 一般可用于numpy的array和ndarray, pandas的dataframe和series(series需要先用series.values把对象转化成ndarray结构)
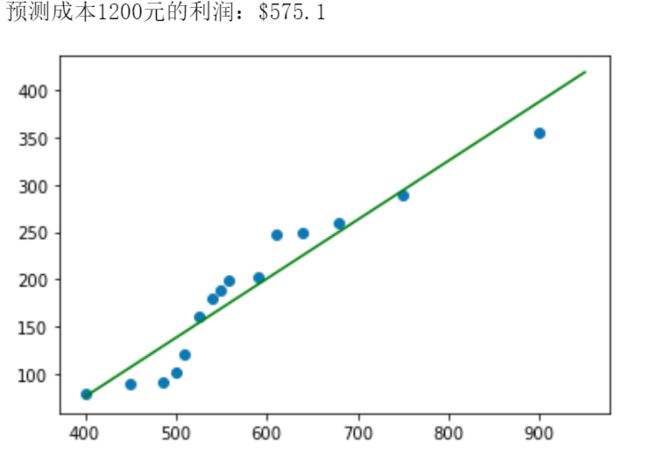
print('预测成本1200元的利润：$%.1f' % res) 

#绘制线性回归图形
#plt.plot(X, Y, 'ks')                 #绘制训练数据集散点图
plt.scatter(X, Y)
plt.plot(X2, Y2, 'g-')               #绘制预测数据集直线(g-表示输出的直线)
plt.show()

输出为：

线性模型的回归系数会保存在coef_变量中，截距保存在intercept_变量中。clf.score(X, Y) 是一个评分函数，返回一个小于1的得分。代码如下：

clf.coef_
clf.intercept_
clf.score(X, Y)
# 输出为
系数 [[0.62402912]]
截距 [-173.70433124]
评分函数 0.9118311887769117

• 该直线对应的回归函数为：y = 0.62402912 * x - 173.70433885，则预测值X2=400的利润值为Y2=75.9，而X中成本为400元对应的真实利润是Y=80元，预测是基本准确的。

2.线性回归预测糖尿病

• 糖尿病数据集

# Sklearn机器学习包提供了糖尿病数据集（Diabetes Dataset），该数据集主要包括442行数据，10个特征值，
# 分别是：年龄（Age）、性别（Sex）、体质指数（Body mass index）、平均血压（Average Blood Pressure）、
# S1~S6一年后疾病级数指标。预测指标为Target，它表示一年后患疾病的定量指标。
from sklearn import datasets                           # 调用sklearn包中的糖尿病数据集
diabetes = datasets.load_diabetes()                    # 载入数据  
# diabetes.data                                        # 数据  
# diabetes.target                                      # 类标  
print('总行数: ', len(diabetes.data), len(diabetes.target))         
print('特征数: ', len(diabetes.data[0]))          # 每行数据集维数  
print('数据类型: ', diabetes.data.shape)                     
print(type(diabetes.data), type(diabetes.target)) # 输出数据和类标的类型  

# 输出为
总行数:  442 442
特征数:  10
数据类型:  (442, 10)
<class 'numpy.ndarray'> <class 'numpy.ndarray'>

• 代码实现
  将糖尿病数据集划分为训练集和测试集，整个数据集共442行，我们取前422行数据用来线性回归模型训练，后20行数据用来预测。其中取预测数据的代码为diabetes_x_temp[-20:]，表示从后20行开始取值，直到数组结束，共取值20个数。

from sklearn import datasets  
import matplotlib.pyplot as plt  
from sklearn import linear_model
import numpy as np  

# 为了方便可视化画图我们只获取其中一个特征进行实验。
#数据集划分
diabetes = datasets.load_diabetes()                # 载入数据  
diabetes_x_temp = diabetes.data[:, np.newaxis, 2]  # 获取第三个特征  
diabetes_x_train = diabetes_x_temp[:-20]           # 训练样本  
diabetes_x_test = diabetes_x_temp[-20:]            # 测试样本 后20行  
diabetes_y_train = diabetes.target[:-20]           # 训练标记  
diabetes_y_test = diabetes.target[-20:]            # 预测对比标记

#回归训练及预测  
clf = linear_model.LinearRegression()  
clf.fit(diabetes_x_train, diabetes_y_train)        # 训练数据集  
pre = clf.predict(diabetes_x_test)                 # 预测值

#绘图  
plt.title(u'LinearRegression Diabetes')            # 标题  
plt.xlabel(u'Attributes')                          # x轴坐标  
plt.ylabel(u'Measure of disease')                  # y轴坐标    
plt.scatter(diabetes_x_test, diabetes_y_test, color = 'black')  # 散点图   
plt.plot(diabetes_x_test, pre, color='blue', linewidth = 2)     # 预测直线
plt.show()          

输出为：

• 代码优化

# 增加了斜率、 截距的计算，可视化绘图增加了散点到线性方程的距离线，增加了保存图片设置像素代码等。
# 这些优化都更好地帮助我们分析真实的数据集。
from sklearn import datasets
import numpy as np
from sklearn import linear_model
import matplotlib.pyplot as plt

# 第一步 数据集划分
d = datasets.load_diabetes()  # 数据 10*442
x = d.data
x_one = x[:,np.newaxis, 2]    # 获取一个特征 第3列数据
y = d.target                  # 获取的正确结果
x_train = x_one[:-42]         # 训练集X [  0:400]
x_test = x_one[-42:]          # 预测集X [401:442]
y_train = y[:-42]             # 训练集Y [  0:400]
y_test = y[-42:]              # 预测集Y [401:442]

# 第二步 线性回归实现
clf = linear_model.LinearRegression()
# print(clf)                   # 回归模型
clf.fit(x_train, y_train)      # 对训练集X和训练集Y进行训练
pre = clf.predict(x_test)      # 预测值
print('预测结果', pre)
print('真实结果', y_test)
   
# 第三步 评价结果
cost = np.mean(y_test-pre)**2   # 平方差之和
print('平方差计算:', cost)
print('系数', clf.coef_) 
print('截距', clf.intercept_)  
print('方差', clf.score(x_test, y_test))

# 第四步 绘图
plt.plot(x_test, y_test, 'k.')      # 散点图
plt.plot(x_test, pre, 'g-')        # 预测回归直线
# 绘制点到直线距离
for idx, m in enumerate(x_test):
    plt.plot([m, m],[y_test[idx], pre[idx]], 'r-')

# plt.savefig('blog12-01.png', dpi=300) # 保存图片
plt.show()  

输出为：

二、多项式回归(polynomial regression)

1.概念

线性回归研究的是一个目标变量和一个自变量之间的回归问题，但有时候在很多实际问题中，影响目标变量的自变量往往不止一个，而是多个自变量。设计一个目标变量与多个自变量间的回归分析，即多元回归分析。

多项式回归（Polynomial Regression）是研究一个因变量与一个或多个自变量间多项式的回归分析方法。如果自变量只有一个时，称为一元多项式回归；如果自变量有多个时，称为多元多项式回归。在一元回归分析中，如果依变量y与自变量x的关系为非线性的，但是又找不到适当的函数曲线来拟合，则可以采用一元多项式回归。
一元m次多项式方程如下：

2.PolynomialFeatures的使用

class sklearn.preprocessing.PolynomialFeatures(degree=2, interaction_only=False, include_bias=True)
参数说明：

degree表示多项式阶数，一般默认值是2；
interaction_only如果值是true（默认是False），则会产生相互影响的特征集；
include_bias表示是否包含偏差列。

3.二项式回归模型例题

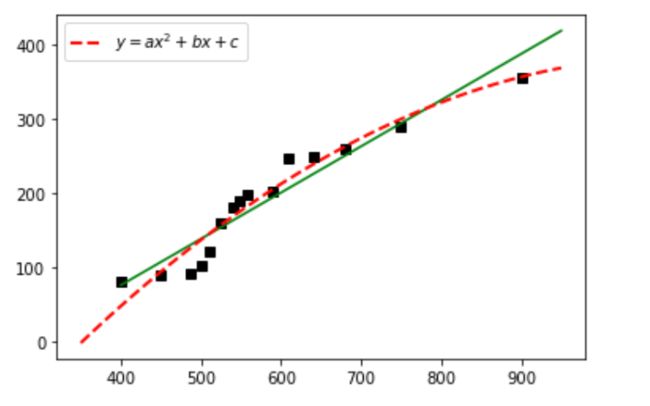
及上述例题中产品成本和利润数据集进行二项式回归分析。

from sklearn.linear_model import LinearRegression    # 导入线性回归模型
from sklearn.preprocessing import PolynomialFeatures # 导入多项式回归模型
import matplotlib.pyplot as plt       
import numpy as np

X = [[400], [450], [486], [500], [510], [525], [540], [549], [558], [590], [610], [640], [680], [750], [900]]
Y = [[80], [89], [92], [102], [121], [160], [180], [189], [199], [203], [247], [250], [259], [289], [356]]
# print('数据集X: ', X)
# print('数据集Y: ', Y)

# 第一步 线性回归分析
clf = LinearRegression() 
clf.fit(X, Y)                     
X2 = [[400], [750], [950]]
Y2 = clf.predict(X2)
# print(Y2)
res = clf.predict(np.array([1200]).reshape(-1, 1)) 
# print('预测成本1200元的利润：$%.1f' % res) 
plt.plot(X, Y, 'ks')    # 绘制训练数据集散点图
plt.plot(X2, Y2, 'g-')  # 绘制预测数据集直线(g-表示输出的直线)

# 重点在第二步 多项式回归分析
xx = np.linspace(350,950,100) # 350到950等差数列
quadratic_featurizer = PolynomialFeatures(degree = 2) # 实例化一个二次多项式特征实例
x_train_quadratic = quadratic_featurizer.fit_transform(X) # 用二次多项式对样本X值做变换    
regressor_quadratic = LinearRegression()                  # 创建一个新的线性回归模型
regressor_quadratic.fit(x_train_quadratic, Y)             # 以多项式变换后的X值为输入，带入线性回归模型做训练

# 把训练好X值的多项式特征实例应用到一系列点上,形成矩阵
xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0], 1))
plt.plot(xx, regressor_quadratic.predict(xx_quadratic), "r--",
         label="$y = ax^2 + bx + c$",linewidth=2)
plt.legend() # 设置图例
plt.show()    

输出为：黑色散点图表示真实的产品成本和利润的关系，绿色直线为一元线性回归方程，红色虚曲线为二次多项式方程。

---

总结

线性回归的优缺点：

优点

• 运算速度快。由于算法很简单，而且符合非常简洁的数学原理，不管是建模速度，还是预测速度都是非常快的。
• 可解释性强。由于最终我们可以得到一个函数公式，根据计算出的公式系数就可以很明确地知道每个变量的影响大小。
• 对线性关系拟合效果好。如果数据是非线性关系，那么就不合适了。

缺点

• 预测的精确度较低。由于获得的模型只是要求最小的损失，而不是对数据良好的拟合，所以精确度略低。
• 不相关的特征会影响结果。对噪声数据也比较难处理，所以在数据处理阶段需要剔除不相关的特征以及噪声数据。
• 容易出现过拟合。尤其在数据量较少的情况下，可能出现这种问题。