机器学习实验 - 逻辑回归
目录
-
- 一、报告摘要
-
- 1.1 实验要求
- 1.2 实验思路
- 1.3 实验结论
- 二、实验内容
-
- 2.1 方法介绍
- 2.2 实验细节
-
- 2.2.1 实验环境
- 2.2.2 实验过程
- 2.2.3 实验与理论内容的不同点
- 2.3 实验数据介绍
- 2.4 评价指标介绍
- 2.5 实验结果分析
- 三、总结及问题说明
- 四、参考文献
- 附录:实验代码
报告内容仅供学习参考,请独立完成作业和实验喔~
一、报告摘要
1.1 实验要求
\qquad 给定一个二分类数据集,编程实现逻辑回归模型,包括数据处理模块、前向计算模块、损失函数模块、梯度计算模块、参数优化模块、预测模块等,使用混淆矩阵评估逻辑回归模型性能表现。
1.2 实验思路
\qquad 使用Python读取German Credit Data数据集并使用梯度下降方法训练一个逻辑回归模型,随后使用生成的模型将数据进行分类预测,并根据精确率、召回率和F1值评测模型性能。
1.3 实验结论
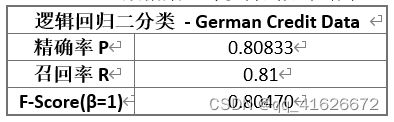
\qquad 本实验训练了一个逻辑回归模型,并对German Credit Data数据集进行分类预测。通过测试,在测试集上取得精确率0.80833、召回率0.81、F1值0.80470的成绩,可以有效完成分类任务。
二、实验内容
2.1 方法介绍
(1)线性回归
\qquad 线性模型是通过属性的线性组合来进行预测的函数,可以表示为:
f ( x ) = w 1 x 1 + w 2 x 2 + . . . + w d x d + b f(x)\ =\ w_1x_1+w_2x_2+...+w_dx_d+b f(x) = w1x1+w2x2+...+wdxd+b
f ( x ) = w T x + b f(x)\ =\ w^Tx+b f(x) = wTx+b
\qquad 回归分析中,如果只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
\qquad 在线性回归中,常采用均方误差衡量预测值与真实值的差别(损失函数),以均方误差最小化,求解最优w和b参数值(目标)。求解过程可以使用最小二乘法来解决,即试图找到一条直线,使得所有样本到直线上的欧式距离之和最小(参数优化问题)。
(2)逻辑回归
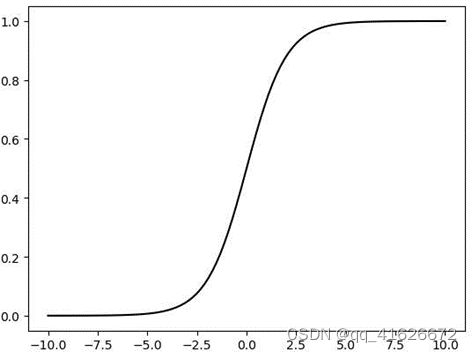
\qquad 逻辑回归是一种广义的线性回归,原因是虽然被称为回归,而且形式也与线性回归的形式基本相同,但逻辑回归完成的是分类任务。简单理解一下,线性回归是用来给出一个值,分类是用来将样本分为几类,那如果将样本进行回归得到一个值,再根据这个值来分类,即使用“线性回归+阈值”来解决分类问题。而具体实践中,由于这个阈值不好准确把握,因此将结果映射到一个(0,1)的区间内进行判断,这个对于连续值进行压缩变换的函数就是Sigmoid函数,数学表达式为
S ( x ) = 1 1 + e − x S\left(x\right)=\frac{1}{1+e^{-x}} S(x)=1+e−x1
\qquad 下面需要找一个决策边界,也就是分类器用于样本区分的边界来完成类别的判定。决策边界由给出的参数决定,而决策边界的确定又可以直接影响分类器的性能。因此需要对参数进行优化,使得整个分类器得到一个较好的分类效果,这也就是参数优化问题。
\qquad 我们使用损失函数来衡量模型的好坏,因此参数优化问题变成了:找到一组参数,使得损失函数最小,此时即为最优解。在逻辑回归中,一般采用极大似然估计作为损失函数,即找到一组参数,使得在这组参数下,我们的数据的似然度(概率)最大。具体的推导过程如下:
\qquad 已知,最大似然估计的函数形式为: L ( w , b ) = ∏ i = 1 N P ( y i ∣ x i ; w , b ) L(w,\ b)\ =\ \prod_{i=1}^{N}{P(y_i|x_i;w,b)} L(w, b) = ∏i=1NP(yi∣xi;w,b),最大对数似然估计的函数为: L ( w , b ) = ∑ i = 1 N l n P ( y i ∣ x i ; w , b ) L(w,\ b)\ =\ \sum_{i=1}^{N}{lnP(y_i|x_i;w,b)} L(w, b) = ∑i=1NlnP(yi∣xi;w,b)。进一步,将 P ( y i ∣ x i ; w , b ) P(y_i|x_i;w,b) P(yi∣xi;w,b)分为了 P ( y i = 0 ∣ x i ; w , b ) P(y_i=0|x_i;w,b) P(yi=0∣xi;w,b),即
P ( y i ∣ x i ; w , b ) = y i P ( y i = 1 ∣ x i ; w , b ) + ( 1 − y i ) P ( y i = 0 ∣ x i ; w , b ) P(y_i|x_i;w,b)=y_iP(y_i=1|x_i;w,b)+(1-y_i)P(y_i=0|x_i;w,b) P(yi∣xi;w,b)=yiP(yi=1∣xi;w,b)+(1−yi)P(yi=0∣xi;w,b)
P ( y i = 0 ∣ x i ; w , b ) = 1 − P ( y i = 1 ∣ x i ; w , b ) P(y_i=0|x_i;w,b)=1-\ P(y_i=1|x_i;w,b) P(yi=0∣xi;w,b)=1− P(yi=1∣xi;w,b)
\qquad 代入 L ( w , b ) L(w,\ b) L(w, b),有:
L ( w , b ) = ∑ i = 1 N y i l n ( P ( y i = 1 ∣ x i ; w , b ) ) − ( 1 − y i ) l n ( 1 − P ( y i = 1 ∣ x i ; w , b ) ) L(w,\ b)\ =\ \sum_{i=1}^{N}y_iln(P(y_i=1|x_i;w,b))-({1-y}_i)ln(1-P(y_i=1|x_i;w,b)) L(w, b) = i=1∑Nyiln(P(yi=1∣xi;w,b))−(1−yi)ln(1−P(yi=1∣xi;w,b))
\qquad 上式的概率最大化等价于最小化,故有损失函数
L ( w , b ) = ∑ i = 1 N − l n ( P ( y i = 1 ∣ x i ; w , b ) ) + ( 1 − y i ) l n ( 1 − P ( y i = 1 ∣ x i ; w , b ) ) \ L(w,\ b)\ =\ \sum_{i=1}^{N}-ln(P(y_i=1|x_i;w,b))+({1-y}_i)ln(1-P(y_i=1|x_i;w,b)) L(w, b) = i=1∑N−ln(P(yi=1∣xi;w,b))+(1−yi)ln(1−P(yi=1∣xi;w,b))
\qquad 参数优化问题常见的优化算法之一是“梯度下降法”。梯度下降法,是一个一阶最优化算法,通常也称为最速下降法。要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。梯度下降法的算法如下:

2.2 实验细节
2.2.1 实验环境
硬件环境:Intel® Core™ i5-10300H CPU + 16G RAM
软件环境:Windows 11 家庭中文版 + Python 3.8
2.2.2 实验过程
(1)数据处理模块
\qquad 本次实验数据采用UCI提供的German Credit Data数据集,由于数据量纲并不统一,为了提升准确率,读取数据后,需要对标签以外的数据进行归一化处理。具体代码如下:
def load_data(): # 数据预处理:读取+归一化
data = np.loadtxt("german.data-numeric") # 读入数据
n, l = data.shape
for j in range(l-1): # 归一化
meanVal = np.mean(data[:, j])
stdVal = np.std(data[:, j])
data[:, j] = (data[:, j]-meanVal) / stdVal
X = data[:,:l-1] # 记得-1,Sigmoid是0/1
y = data[:,l-1]-1
return X,y
(2) 前向计算模块
\qquad 前计算模块的主要功能为计算当前结果对应的Sigmoid值,直接根据Sigmoid函数公式进行编写:
def sigmoid(t): # 前向传播模块
return 1. / (1. + np.exp(-t))
(3) 损失函数模块
\qquad 根据2.1部分的分析,在逻辑回归中,一般使用最大似然估计作为损失函数,根据推导得到的公式进行代码编写。为了方便后续梯度下降法优化参数,这里一并给出求导后的函数。
def J(theta, X_b, y): # 损失函数
y_hat = sigmoid(X_b.dot(theta))
try:
return -np.sum(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat)) / len(y)
except:
return float('inf')
def dJ(theta, X_b, y): # 求导
return X_b.T.dot(sigmoid(X_b.dot(theta)) - y) / len(y)
(4) 梯度计算模块
\qquad 根据梯度下降法的思想,通过不断的梯度下降找到损失函数的最小值即可。这里为了控制计算次数,引入了两个控制条件:maxloop和epsilon,分别用于控制最大循环次数和每次循环的精度。
def gradient_descent(X_b, y, initial_theta, eta, maxloop=1e4, epsilon=1e-8): # 梯度计算模块
theta = initial_theta
now_loop = 0
while now_loop < maxloop:
gradient = dJ(theta, X_b, y)
last_theta = theta
theta = theta - eta * gradient
if abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon:
break
now_loop += 1
return theta
(5) 参数优化模块
def fit(X_train, y_train, eta=0.01, maxloop=1e4): # 参数优化模块
global _theta,intercept,coef # 声明全局变量
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
initial_theta = np.zeros(X_b.shape[1])
_theta = gradient_descent(X_b, y_train, initial_theta, eta, maxloop) # 参数
# 截距
intercept = _theta[0]
# x_i前的参数
coef = _theta[1:]
(6) 预测模块
\qquad 由于逻辑回归其实可以理解为“先回归,再分类”,因此我们这里也根据这个理解完成获取回归值的函数,以及根据回归值判断分类的方法。
def predict_proba(X_predict): # 预测回归值
global _theta,intercept,coef # 声明全局变量
X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
return sigmoid(X_b.dot(_theta))
def predict(X_predict): # 预测分类
global _theta,intercept,coef # 声明全局变量
prob = predict_proba(X_predict)
return np.array(prob >= 0.5, dtype='int')
2.2.3 实验与理论内容的不同点
\qquad 实验与理论内容的主要区别在数据的预处理以及梯度下降的实现上。
\qquad 由于Sigmoid函数在(0,1)区间上,且二分类的结果为0或1。因此,用于训练和使用的数据集也应该将分类结果映射到0或1两种情况。在本次使用的数据集中,标签为1或2,因此需要在读取数据时进行预处理。
\qquad 梯度下降法具体实现时,添加了另外两个控制条件:maxloop和epsilon,分别用于控制最大循环次数和每次循环的精度。最大循环次数相对好理解,用于跳出死循环或接近死循环的过程。引入每次循环的精度是为了阻止系数在最小值附近一直纠结但很难再有大的精进,尽可能保证速度和精度。
2.3 实验数据介绍
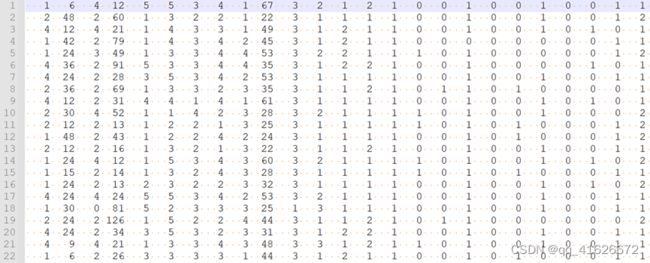
\qquad 实验数据为来自UCI的德国信用数据集German Credit Data。
\qquad 数据集共包含1000组数据。每组数据包括20个参数和1个分类标签,分类标签为是否为风险用户(1为无风险,2为有风险),20个参数分别为:
- 现有支票账户状态
- 信用期限
- 还款状态
- 贷款用途
- 信贷额
- 储蓄账户/债券状态
- 工作年限
- 分期付款占可支配收入百分比
- 性别及婚姻状态
- 担保人
- 当前地址居住时长
- 最有价值的可用资产
- 年龄
- 其他分期付款计划
- 房屋所有权情况
- 本银行信用卡数量
- 职业
- 亲属人数
- 电话
- 是否外国雇员
2.4 评价指标介绍
\qquad 评价指标选择精确率P、召回率R、F1度量值F1,计算公式如下:
P = T P T P + F P P=\frac{TP}{TP+FP} P=TP+FPTP
R = T P T P + F N R=\frac{TP}{TP+FN} R=TP+FNTP
F 1 = 2 ∗ P ∗ R P + R F1=\frac{2*P*R}{P+R} F1=P+R2∗P∗R
\qquad 具体代码实现时,可以直接调用sklearn库中的相应方法进行计算。
print("精确率",precision_score(y_test, y_pred, average='weighted'))
print("召回率",recall_score(y_test, y_pred, average='weighted'))
print("F1度量值",f1_score(y_test, y_pred, average='weighted'))
2.5 实验结果分析
\qquad 将全部的1000条数据随机分为800条训练集,100条验证集和100条测试集。利用测试集进行测试,使用验证集调整相关超参数,最终根据测试集得到的结果计算,对于German Credit Data数据集,可以得到如下结果:
三、总结及问题说明
\qquad 本次实验的主要内容为使用梯度下降法训练逻辑回归模型,实现对德国信用数据集的多元回归预测。
\qquad 在本次实验中,可以通过查阅资料解决实验中产生的问题,并成功完成全部实验任务。
四、参考文献
[1] 周志华. 机器学习[M]. 清华大学出版社, 2016.
[2] API Reference — scikit-learn 1.1.1 documentation [EB/OL]. [2022-5-8]. https://scikit-learn.org/stable/modules/classes.html.
[3] 百面机器学习——python实现二分类逻辑回归[EB/OL]. [2022-5-8]. https://blog.csdn.net/qq_39309652/article/details/104551640.
[4] 【机器学习】逻辑回归(非常详细)[EB/OL]. [2022-5-8]. https://zhuanlan.zhihu.com/p/74874291.
附录:实验代码
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import precision_score, recall_score, f1_score
coef = None # 系数
intercept = None # 截距
_theta = None # 学习率
def load_data(): # 数据预处理:读取+归一化
data = np.loadtxt("german.data-numeric") # 读入数据
n, l = data.shape
for j in range(l-1): # 归一化
meanVal = np.mean(data[:, j])
stdVal = np.std(data[:, j])
data[:, j] = (data[:, j]-meanVal) / stdVal
X = data[:,:l-1] # 记得-1,Sigmoid为0/1
y = data[:,l-1]-1
return X,y
def sigmoid(t): # 前向传播模块
return 1. / (1. + np.exp(-t))
def J(theta, X_b, y): # 损失函数
y_hat = sigmoid(X_b.dot(theta))
try:
return -np.sum(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat)) / len(y)
except:
return float('inf')
def dJ(theta, X_b, y): # 损失函数向量化
return X_b.T.dot(sigmoid(X_b.dot(theta)) - y) / len(y)
def gradient_descent(X_b, y, initial_theta, eta, maxloop=1e4, epsilon=1e-8): # 梯度计算模块
theta = initial_theta
now_loop = 0
while now_loop < maxloop:
gradient = dJ(theta, X_b, y)
last_theta = theta
theta = theta - eta * gradient
if abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon:
break
now_loop += 1
return theta
def fit(X_train, y_train, eta=0.01, maxloop=1e4): # 参数优化模块
global _theta,intercept,coef # 声明全局变量
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
initial_theta = np.zeros(X_b.shape[1])
_theta = gradient_descent(X_b, y_train, initial_theta, eta, maxloop) # 参数
# 截距
intercept = _theta[0]
# x_i前的参数
coef = _theta[1:]
def predict_proba(X_predict): # 预测回归值
global _theta,intercept,coef # 声明全局变量
X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
return sigmoid(X_b.dot(_theta))
def predict(X_predict): # 预测分类
global _theta,intercept,coef # 声明全局变量
prob = predict_proba(X_predict)
return np.array(prob >= 0.5, dtype='int')
X,y = load_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
fit(X_train, y_train)
y_pred = predict(X_test)
print("精确率",precision_score(y_test, y_pred, average='weighted'))
print("召回率",recall_score(y_test, y_pred, average='weighted'))
print("F1度量值",f1_score(y_test, y_pred, average='weighted'))