机器学习-监督学习及典型算法

监督学习(Supervised)

​ 监督学习是目前运用最广泛的一种ML方法。如BP、决策树。监督学习通过训练既有特征又有鉴定标签的训练数据，让机器学习特征与标签之间产生联系。在训练好之后，可以预测只有特征数据的标签。监督学习可分为回归(Regression)分析和分类(Classification)。

​ 回归分析：对训练数据进行分析，拟合出误差最小的函数模型y=f(x)，这里的y就是数据的标签，而对于一个新的自变量x，通过这个函数模型得到标签y。

​ 分类：训练数据是特征向量与其对应的标签，同样通过计算新的特征向量得到所属的标签。

在拿到一个问题时，首先要先区别这是一个回归分析的问题还是一个分类的问题。

例如：根据已被诊断出是否患有无糖尿病的病人信息，判断新的病人是否患有糖尿病

原理

​ 监督学习假设训练数据与真实预测数据属于同一概率分布并且相互独立。监督学习通过训练学习到数据的概率分布，并应用到真实的预测上。

输入空间、特征空间、输出空间

​ 输入空间与输出空间可以相同也可以不同，通常下输出空间远小于输入空间。每一个具体的输入被称作实例、由特征向量表示。所有特征向量组成特征空间，特征空间的每一维代表一个特征。

​ 回归问题：输入变量与输出变量均为连续变量的预测问题。

​ 分类问题：输出变量是有限个离散变量的预测问题。

​ 标注问题：输入变量与输出变量均为变量序列的预测问题。

\\\\\\

KNN算法(K-Nearest Neighbor Classification)

​ 简而言之：周围什么多它就是什么，没有学习的过程，不适合BP。

​ KNN，K近邻算法，根据不同特征值之间的距离来进行分类的ML算法。该算法的主要应用领域是对未知事物进行分类(判断未知事物属于哪一类)。KNN也可用于回归，通过找出一个样本的k个最近邻居，将这些邻居属性的平均值赋给该样本，就i可以得到该样本的属性。

​ KNN算法的原理是：将测试数据的特征与训练集中对应的特征进行比较，找到训练集中最为相似的前K个数据，则该测试数据对应的类别就是K个数据中出现次数最多的那个分类。

计算测试数据与各个训练数据之间的距离。

按照距离的递增关系排序。

选取距离最小的K个点、确定前k个点所在类别的出现频率。

选择出现频率最高的作为测试数据的预测分类。

​ 这里说的距离与K参数的选取直接决定算法的效果。KNN的距离指的是：设定X实例以及Y实例均包含了N维的特征，即$X=(x_1,x_2,\cdot \cdot \cdot ,x_n),Y=(y_1,y_2,\cdot \cdot \cdot ，y_n)$。度量二者的差异，主要由距离度量和相似度度量两类。

①距离度量

②相似度度量

个人想法：有一定的用处，但是准确率貌似不咋样。没什么可以提高的方法（是因为KNN没有学习的过程）。

\\\\\\

近似误差与估计误差：

近似误差：对现有训练集的训练误差，关注训练集，如果近似误差过小可能会出现过拟合的现象，对现有的训练集能有很好的预测，但是对未知的测试样本将会出现较大偏差的预测。模型本身不是最接近最佳模型。

估计误差：可以理解为对测试集的测试误差，关注测试集，估计误差小说明对未知数据的预测能力好，模型本身最接近最佳模型。

K值确定标准：

​ 如果选择较小的K值：就相当于用较小的邻域中的训练实例进行预测，学习的近似误差会减小，只有与输入实例较近的训练实例才会对预测结果起作用，缺点是学习的估计误差会增大，预测结果会对近邻的实例点分敏感。*如果邻近的实例点恰巧是噪声，预测就会出错。*换句话说，K值减小就意味着整体模型变复杂，分不清楚，易发生过拟合。

​ 如果选择较大K值：就相当于用较大邻域中的训练实例进行预测，其优点是可以减少学习的估计误差，但近似误差会增大，也就是对输入实例预测不准确，K值得增大就意味着整体模型变的简单。

实例：

import numpy as np
from sklearn import neighbors

knn = neighbors.KNeighborsClassifier()
data = np.array([[3,104],[2,100],[1,81],[101,10],[99,5],[98,21]])
sample=np.array([[10,92]])
labels = np.array([1,1,1,2,2,2])
knn.fit(data,labels)
print(knn.predict(sample))
//输出  [1]

\\\\\\
\\\\\\

支持向量机(SVM)

​ SVM算法是基于统计学习理论的一种ML方法，它通过寻求结构化风险最小化来提高学习器的繁华能力，实现经验风险和置信范围的最小化，从而达到在样本较少的情况下也能获得良好统计规律的目的。如今常用于对小样本、非线性及高维数据进行模式识别、分类以及回归分析，并能取得良好效果。

​ SVM是一个二分类的分类模型。给定一个包含正反例（正负样本点）的样本集合，SVM会寻找一个超平面来对样本进行分割，把样本中的正反例用超平面进行分开，并使正反例之间的间隔最大。（一般将任何维的分类边界都称为超平面）

​ 其核心思想为：

① SVM算法是针对线性可分情况进行分析；对于线性不可分的情况，通过使用非线性映射算法将低维输入空间线性不可分的样本转化为高维特征空间线性可分，从而使得对样本的非线性特性进行线性分析称为可能。

② SVM算法以结构风险最小化在特征空间中构建最优分割超平面，使得学习器得到全局最优。

​

​ 学习的目标是在特征空间内找到**一个分类超平面 **$\mathbf{w}x+b=0$，分类超平面将特征空间划分为两部分（正类、负类）。

我认为这个算法最重要的应该就是找到这个超平面、就像KNN最重要的是找到它画圈的半径这样？（不知道举例准不准）

注意此处的w：并不是指直线，而是一个集合（反正我这么称呼）、

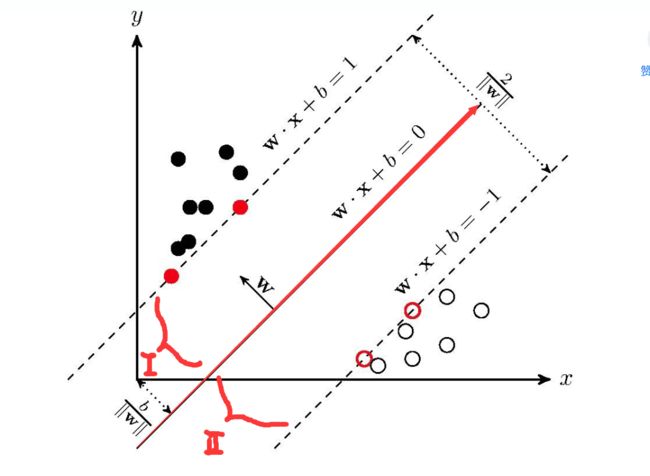
​ 我的理解是：如果我们想要找到这个超平面，可以使用凸二次规划来解决。关于凸二次规划的学习:【 凸集、凸函数、凸优化和凸二次规划】*。凸函数在数学分析中被介绍，果然被广泛运用于很多方面，是一个很有用的函数！*此处的约束条件是：Ⅰ区内无正样本点、Ⅱ区内无负样本点。

​ 对它的处理是使用高数中我们学习过的拉格朗日乘法。后面的处理过程我就不赘述了，毕竟别人写得更好orz

【安利一篇关于SVM超平面推导过程的知乎文章】

这个是我找到的最清晰易懂的KKT条件的介绍：【 Karush-Kuhn-Tucker (KKT)条件 - 知乎】

​ 在线性不可分的情况下，SVM现在低维空间中完成计算，再通过核函数映射到高位特征空间，最终在高维特征空间中构造出最优分离超平面，从而把屏幕上本身不好分的非线性数据分离开。

核函数是？相当于相似度函数方程。通过标记点和相似性函数来定义新的特征变量，从而训练出复杂得到非线性边界。

核函数主要使用于复杂的非线性数据的分类问题。**但是我们从哪得到标记点？**将选取我们拥有的每一个样本点作为标记点。

偏差方差分析：

当 C ($\frac{1}{\lambda }$)和 σ 取值较大时：会发生过拟合、偏差小、方差大；（正态分布函数较为尖锐）

当 C ($\frac{1}{\lambda }$)和 σ 取值较小时：会发生欠拟合、偏差大、方差小；（正态分布函数较为平缓）

如何选择使用SVM还是逻辑回归？

当样本特征的数量远大于样本的数量：基本上使用逻辑回归或是线性核函数（无核SVM）；

反之，样本特征的数值是一个大小适中，m也大小适中，使用高斯SVM；

如果样本特征的数量很小，样本数量很大，此时如果还选择高斯SVM，运行速度会很慢，基本上使用逻辑回归或是线性核函数（无核SVM）。(并自己手动添加一些样本特征)

实例：

from sklearn import svm
import numpy as np
import  matplotlib.pyplot as plt

# 设置子图数量
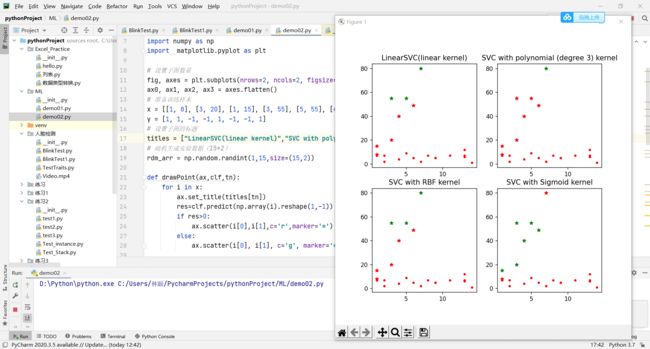
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(7,7))
ax0, ax1, ax2, ax3 = axes.flatten()
# 准备训练样本
x = [[1, 8], [3, 20], [1, 15], [3, 55], [5, 55], [4, 40], [7, 80], [6, 49]]
y = [1, 1, -1, -1, 1, -1, -1, 1]
# 设置子图的标题
titles = ["LinearSVC(linear kernel)","SVC with polynomial (degree 3) kernel","SVC with RBF kernel","SVC with Sigmoid kernel"]
# 随机生成实验数据（15*2）
rdm_arr = np.random.randint(1,15,size=(15,2))

def drawPoint(ax,clf,tn):
    for i in x:
        ax.set_title(titles[tn])
        res=clf.predict(np.array(i).reshape(1,-1))
        if res>0:
            ax.scatter(i[0],i[1],c='r',marker='*')
        else:
            ax.scatter(i[0], i[1], c='g', marker='*')

    for i in rdm_arr:
        res=clf.predict(np.array(i).reshape(1,-1))
        if res>0:
            ax.scatter(i[0],i[1],c='r',marker='.')
        else:
            ax.scatter(i[0], i[1], c='g', marker='.')

# 主函数
if __name__ == "__main__":
    # 选择核函数
    for n in range(0,4):
        if n == 0:
            clf = svm.SVC(kernel="linear").fit(x,y)
            drawPoint(ax0,clf,0)
        elif n == 1:
            clf = svm.SVC(kernel="poly",degree=3).fit(x, y)
            drawPoint(ax1, clf, 1)
        elif n == 2:
            clf = svm.SVC(kernel="rbf").fit(x, y)
            drawPoint(ax2, clf, 2)
        else:
            clf = svm.SVC(kernel="sigmoid").fit(x, y)
            drawPoint(ax3, clf, 3)

    plt.show()

乍一看上去，感觉是不是好像不一样？

但是实际上：虽然分类的标准不一样，但是对于随机出来的点得到的分类结果是一样的。

\\\\\\
\\\\\\

朴素贝叶斯分类(Nave Bayes)

​ 对于朴素贝叶斯来说：最重要的就是它把每个输入变量都设为独立的。

​ 假设有训练数据集合，其中特征向量$X=(x_1,x_2,\cdot \cdot \cdot ,x_n)$对应分类变量y，可以使用贝叶斯理论：$P(y|X)=P(X|y)P(y)P(X)$。朴素贝叶斯的思想基础是这样的：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。

对于朴素贝叶斯，一共分为两种概率：

1. 每个类别的概率$P(C_j)$ 例：患新冠与否

2. 每个属性的条件概率$P(A_i,C_j)$ 例：检测核酸样本呈阳性/阴性

   （对于检测的核酸样本来说：有可能出现假阳的情况：即检测结果为阳性，但实际上没有患病）

​ 对于朴素贝叶斯分类来说，我们将其一共分为三个阶段：

1. 准备阶段：在这个阶段我们需要确定特征属性，比如上面案例中的“身高”、“体重”、“鞋码”等，同时明确预测值是什么。并对每个特征属性进行适当划分，然后由人工对一部分数据进行分类，形成训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段，其质量对整个过程将有重要影响，分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。

2. 训练阶段：这个阶段就是生成分类器，主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率。输入是特征属性和训练样本，输出是分类器。

3. 应用阶段：这个阶段是使用分类器对新数据进行分类。输入是分类器和新数据，输出是新数据的分类结果。

总结：
朴素贝叶斯分类常用于文本分类，尤其是对于英文等语言来说，分类效果很好。它常用于垃圾文本过滤、情感预测、推荐系统等。

优点：

1. 朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
2. 对小规模的数据表现很好，能个处理多分类任务，适合增量式训练，尤其是数据量超出内存时，我们可以一批批的去增量训练。
3. 对缺失数据不太敏感，算法也比较简单，常用于文本分类。

缺点：

1. 理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
2. 需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
3. 由于我们是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。
4. 对输入数据的表达形式很敏感。

emmm 没有实例啦，找到一组讲解的朴素贝叶斯实现算法，非常详细，推荐阅读。

【朴素贝叶斯算法 — 超详细公式讲解+代码实例】

\\\\\\

\\\\\\

决策树算法

​ 决策树学习是根据数据的属性采用的树状结构建立的决策模型，可以用此模型解决分类和回归问题。**决策树算法指的是：对数据特性进行划分的时候选取最优特征的算法，将无序的数据尽量变得更加有序。**常见的算法包括：CART、ID3、C4.5等。

​ 决策树的决策选择最优特征常用的3个度量为：信息增益(Information Gain)、增益比率(Gain Ratio)、基尼不纯度(Gini Impurity)。

信息增益

​ 用划分前集合与划分后集合之间的信息熵差值来衡量当前特征对于样本集合划分的效果。

信息熵：在信息论种代表随机变量不确定的度量。越不确定的事物，它的熵就越大。随机变量X的熵表达式为：
$$H(X)=-\sum _{x\in X}p(x)\log p(x)$$
条件熵：设X和Y是两个离散型的随机变量，随机变量X给定的条件下随机变量Y的条件熵$H(Y|X)$表示在已知随机变量X的条件下随机变量Y的不确定性。

信息增益：$Entroy(前)-Entroy(后)$，其计算公式如下：
$$Gain(S,T)=IG(S,T)=H(S)-\sum _{v\in value(T)}\frac{S_v}{S}H(S_v)$$
S：全部样本集合、value(T)：属性划分后T所有取值的集合、v是T的其中一个属性值。

$S_V$是S中属性T的值为v的样例集合，$|S_v|$为$S_v$中所含样例数。

信息增益率：

​ 节点信息增益与节点分裂信息度量的比值。信息增益率是C4.5算法的基础。信息增益率度量是用增益度量$Gain(S,T)$和分裂信息度量$SplitInfotmation(S,T)$来共同定义的。分裂信息度量$SplitInfotmation(S,T)$就相当于特征T的熵。
KaTeX parse error: Undefined control sequence: \abs at position 101: …_{i=1}^c \frac{\̲a̲b̲s̲{S_i}}{\abs{S}}…
基尼不纯度：

​ 衡量集合的无序程度，表示在样本集合中一个随机选中的样本被分错的概率。($f_i$是样本i出现的概率)
$$I_G(f)=\sum _{i=1}^m{f}_i(1-f_i)=\sum _{i=1}^m{f}_i-\sum _{i=1}^m{f}_i^2=1-\sum _{i=1}^m{f}_i^2$$

1. 基尼不纯度越小，纯度越高，集合的有序程度越高，分类的效果越好。
2. 基尼不纯度为0时，表示集合类别一致，仅有唯一的类别。
3. 基尼不纯度最高(纯度最低)时，$f_1=f_2=\cdot \cdot \cdot =f_m$，$I_G(f)=1-m\ast (\frac{1}{m}{)}^2=1-\frac{1}{m}$。

对于ID3算法：使用最大信息增益构造决策树。因为信息增益越大，就越能减少不确定性，区分样本的能力就越强，越具有代表性。所以，ID3算法在决策树的每一个非叶子结点划分之前，先计算一个属性带来的信息增益，选择最大的信息增益来区分。

ID3实例：

import pydotplus
import csv
from sklearn import preprocessing
from sklearn import tree
from sklearn.feature_extraction import DictVectorizer

film_data=open('test01.csv','rt')
reader=csv.reader(film_data)
# 表头信息
headers=next(reader)
# print(headers)

feature_list =[]
result_list=[]

for row in reader:
    result_list.append(row[-1])# 保留了最后的结果
    feature_list.append(dict(zip(headers[1:-1],row[1:-1])))# 只保留了中间的类别信息
# 打印输出查看结果
# print(result_list)
# print(feature_list)
# 将dict类型的list数据转换为numpy array
vec = DictVectorizer()
dummyX = vec.fit_transform(feature_list).toarray()
dummyY = preprocessing.LabelBinarizer().fit_transform(result_list)
print(dummyX)# 注意这个是按照首字母来排序的 “country”、"gross"、“type”
print(dummyY)

clf = tree.DecisionTreeClassifier(criterion='entropy', random_state=0)
clf = clf.fit(dummyX,dummyY)
print(clf)

dot_data=tree.export_graphviz(clf,feature_names=vec.get_feature_names(),filled=True,rounded=True,special_characters=True,out_file=None)
graph = pydotplus.graph_from_dot_data(dot_data)

# 开始预测
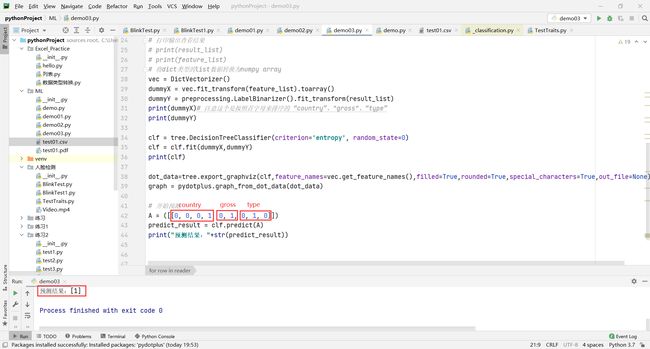
A = ([[0, 0, 0, 1, 0, 1, 0, 1, 0]])
predict_result = clf.predict(A)
print("预测结果："+str(predict_result))

csv文件：

id,type,country,gross,watch
1,anime,Japan,low,yes
2,science,America,low,yes
3,anime,America,low,yes
4,action,America,high,yes
5,action,China,high,yes
6,anime,China,low,yes
7,science,France,low,no
8,action,China,low,no

实验结果: