python统计(一)描述性统计与参数估计
连续型数据的描述
pandas.DataFrame.describe()
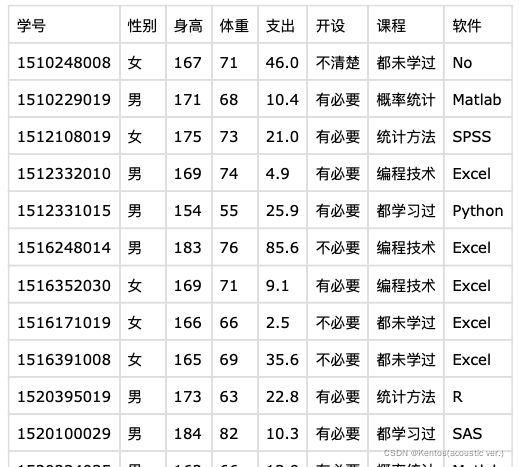
对数值型数据进行描述,包括个数、均值、标准差、最小值、分分位数和最大值
import pandas as pd
df = pd.read_csv(r'/.../bs_data.csv')
df.describe() #首先将数字作为数值型数据处理bs_data.scv
也可以用单独的方法描述各个总体的参数(都是DataFrame和Series的自带方法)
极差
均值
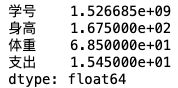
df['身高'].mean()
df.mean(axis=1) # 默认axis=0统计列的数据,axis=1是行中位数
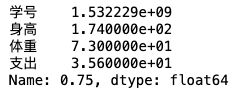
df.median() # 默认描述所有数值型字段,也可以指定字段众数
from scipy import stats
stats.mode(df['身高'])![]()
*返回值是一个元组,包括众数和它的频数
分位数
df.quantile(q=0.75) # q参数用于指定分位位置(0<=q<=1)方差
df['身高'].var()标准差
df['身高'].std()偏度
如果一组数据的分布是对称的,则偏态系数等于0;
大于零为左偏分布,小于零为右偏分布;
若偏态系数绝对值大于1,称为高度偏态分布,绝对值越小,偏斜程度就越低。
df['身高'].skew()峰度
标准正态分布的峰度系数为0;
K>0时为尖峰分布,数据的分布更集中,K<0时为扁平分布,数据的分布越分散;
*有一些定义里标准正态分布的峰度系数是3,pandas里采用的是0的说法
df['身高'].kurt()应用
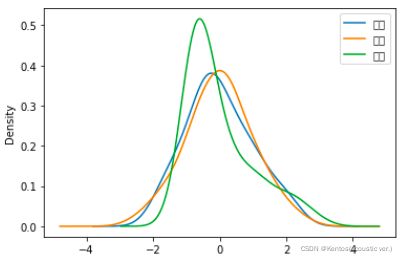
df_sel = df[['身高','体重','支出']]
df_sel = (df_sel-df_sel.mean())/df_sel.std() # 标准化
df_sel.plot(kind='kde')离散型数据的描述
离散型数据包括分类数据和离散型数值数据
describe()方法(含众数)
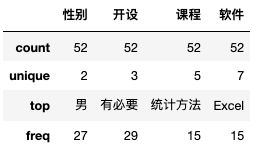
- count:总数;unique:种类数
- top:众数;freq:众数的频数
df[['性别','开设','课程','软件']].describe()频数
df['性别'].value_counts() # 按类别进行计数频率
pandas没有直接计算频率的方法,需要自己计算
df['性别'].value_counts()/df['性别'].count()*100 # 百分制随机变量
scipy的stats模块包含了多种概率分布的随机变量;
- norm:正态分布
- chi2:卡方分布
连续随机变量是rv_continuous 的派生类的对象, 离散随机变量是rv_discrete 的派生类的对象
连续性随机变量
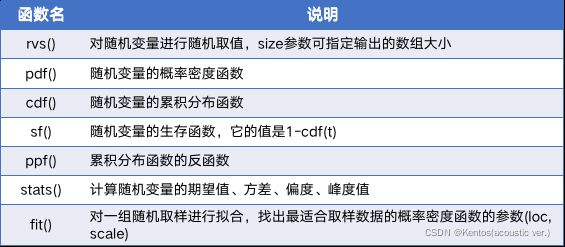
连续性随机变量提供的方法
实例一
from scipy import stats
import seaborn as sns
dl1 = stats.norm.rvs(size=100) # norm为正态分布
sns.displot(dl1)
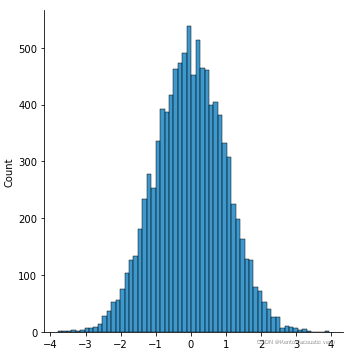
dl2 = stats.norm.rvs(size=10000) # 样本量越大越接近标准正态分布
sns.displot(dl2)*样本量越大越接近正态分布
实例二
loc和scale参数:实现随机变量的偏移和缩放,对于正态分布的随机变量而言,loc参数相当于指定其期望值,scale参数相当于指定其标准差
size=10000
d1 = stats.norm.rvs(size=size) # 默认是标准正态分布
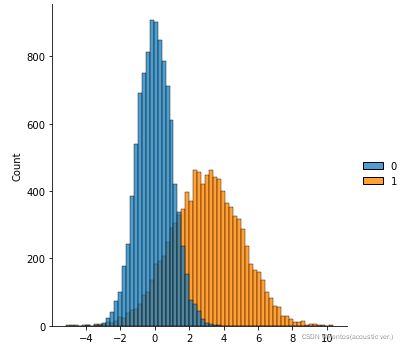
d2 = stats.norm.rvs(loc=3,scale=2,size=size)
ax = sns.displot([d1,d2],alpha=0.7)实例三
d1 = stats.chi2.rvs(df=2,size=size) # chi2为卡方分布,df为自由度
ax = sns.kdeplot(d1)
d2 = stats.chi2.rvs(df=4,size=size)
ax = sns.kdeplot(d2,ax=ax) # 画在同一张图里
d3 = stats.chi2.rvs(df=20,size=size)
ax = sns.kdeplot(d3,ax=ax)*自由度越大,越接近正态分布
实例四
rv = stats.norm(loc=5,scale=3)
rv.cdf(10) # 随机变量的累积分布函数
rv.cdf(10)-rv.cdf(2)离散型随机变量
保留了大部分连续型随机变量的函数;
pdf函数被pmf(probability mass function)函数替代(离散型随机变量的概率质量函数);
函数没有scale参数,但保留了loc参数以指定随机变量的偏移。
二项分布
伯努利实验:独立重复实验
stats.binom.pmf(2,n=3,p=0.05) # 单次实验抽中的概率为0.05,重复3次,抽中2次的概率泊松分布
当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似
其中mu = np
rv = stats.poisson(mu=2.5) # 返回满足这个分布的随机变量对象
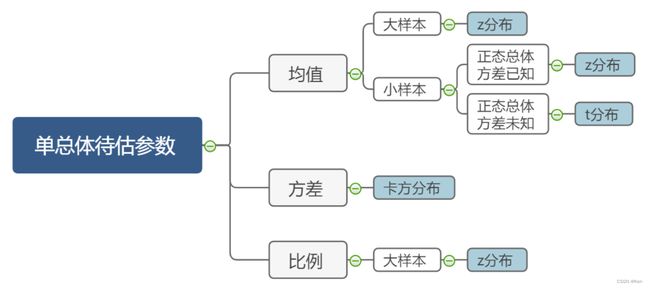
rv.pmf(5) # 发生5次参数估计
scipy.stats
interval()
stats模块里所有随机变量都有的函数求置信区间的方法,参数是置信水平
课堂练习一中有示例
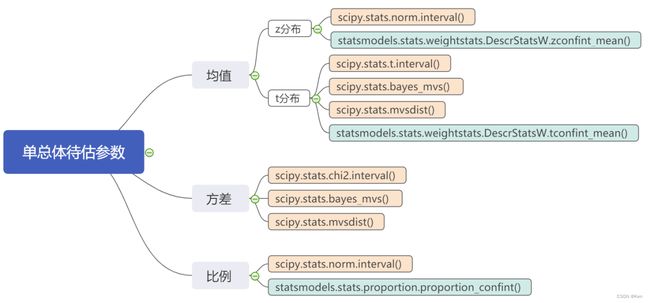
scipy.stats.bayes_mvs(data, alpha=0.9)
提供了方差、标准差以及采用t分布下均值的点估计和区间估计结果
data:接收一维数据,如果传入多维数据,将被展开为一维数据;alpha:置信度
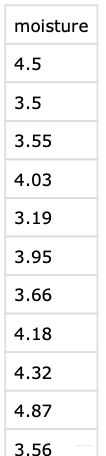
df = pd.read_csv(r'/.../moisture.csv')
# m: mean; v: var; s: std
m,v,s = stats.bayes_mvs(df['moisture'],alpha=0.95)
m
# m.statistic 点估计
# m.minmax 区间估计moisture.csv
返回值(mean_cntr, var_cntr, std_cntr)
元组中的每一个元素都具有如下形式:(center, (lower, upper))其中:center是点估计量;(lower, upper)是区间估计值
![]()
stats.mvsdist()函数
提供了对方差、标准差以及采用t分布下均值进行参数估计的对象
返回值(mdist, vdist, sdist)为三个对象
m,v,s = stats.mvsdist(df['moisture'])
v.mean() # 方差的点估计量
m.interval(0.95) # 均值的置信区间
m.std() # 均值估计的标准误差statsmodels
DescrStatsW(data, weights=None, ddof=0)
data: 输入数据,1维或2维数据; weights: 各样本的权重,可选参数; ddof: 自由度
import statsmodels.api as sma
d = sma.stats.DescrStatsW(df['moisture'])
d.mean() # 点估计
# 区间估计
d.tconfint_mean(alpha=0.05) # 以t分布估计
d.zconfint_mean(alpha=0.05) # 以z分布估计proportion_confint()比例估计
statsmodels.stats.proportion.proportion_confint(count, nobs, alpha=0.05, method='normal')
count:表示“成功”的样本数; nobs:样本总数; alpha:置信度
sma.stats.proportion_confint(count=95, nobs=100, alpha=0.01)课堂练习一
import pandas as pd
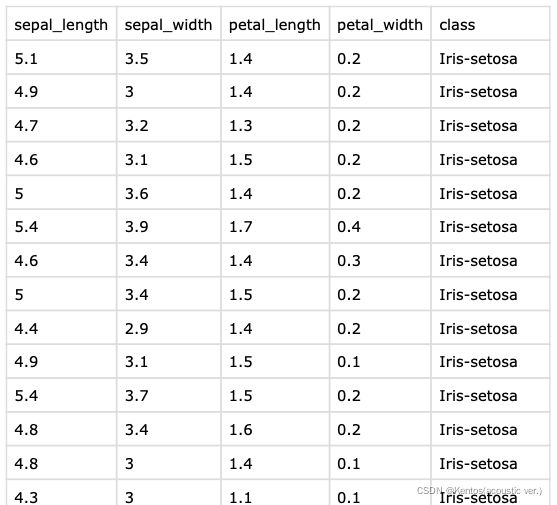
df = pd.read_csv(r'/.../iris.csv')
m,v,s = stats.mvsdist(df['sepal_length'])
m.interval(0.95)iris.csv
![]()