《深度学习入门:基于python的理论与实现》学习笔记
感知机
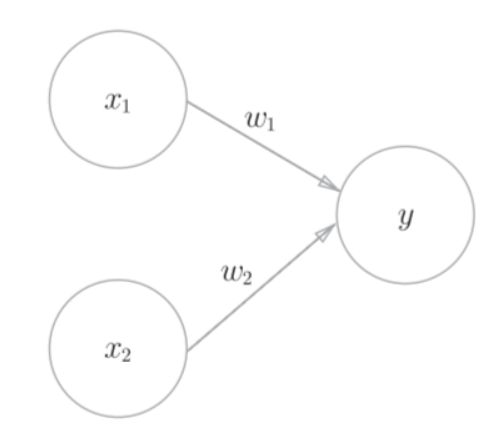
感知机的模型是神经网络的起源算法,也可以帮助我理解神经网络
感知机的大致结构
与门的实现
def AND(x1,x2):
w1,w2 = 0.5,0.5
theta = 0.7
if w1*x1+w2*x2 > theta:
return 1
else :
return 0
print(AND(1,0))
print(AND(1,1))
0
1
引入偏置b和权重
偏置的作用是在x*w之后再加上一个常数,这相当于给了感知机一个基础的值,使得感知机更容易或者更难被激活
import numpy as np
x = np.array([0,1])
w = np.array([0.5,0.5])
b = - 0.7 #这里的b就是偏置,其值为负,使得感知机更难被激活
print(x*w) #[0. 0.5]
print(np.sum(x*w)+b) #-0.19999999999999996
[0. 0.5]
-0.19999999999999996
使用权重和偏置实现与门
在这里,我们对theta进行移项,将等式化为 w*x - b > 0 的形式
def AND2(a,b):
x = np.array([a,b])
w = np.array([0.5,0.5])
b = -0.7
if (np.sum(x*w)+b)>0:
return 1
else:
return 0
print(AND2(1,0)) #0
print(AND2(1,1)) #1
0
1
使用感知机实现与非门和或门
def NAND(a,b):
x = np.array([a,b])
w = np.array([-0.5,-0.5])
b = 0.7
if (np.sum(x*w)+b)>0:
return 1
else:
return 0
def OR(a,b):
x = np.array([a,b])
w = np.array([0.5,0.5])
b = -0.3
if (np.sum(x*w)+b)>0:
return 1
else:
return 0
print(NAND(0,1)) # 1
print(NAND(1,1)) # 0
print(NAND(0,0)) # 1
print(OR(0,1)) # 1
print(OR(0,0)) # 0
1
0
1
1
0
使用感知机实现异或门
def XOR(a,b):
temp = OR(AND2(1-a,b),AND2(a,1-b))
if temp>0:
return 1
else:
return 0
print(XOR(0,1))
print(XOR(1,0))
print(XOR(0,0))
print(XOR(1,1))
1
1
0
0
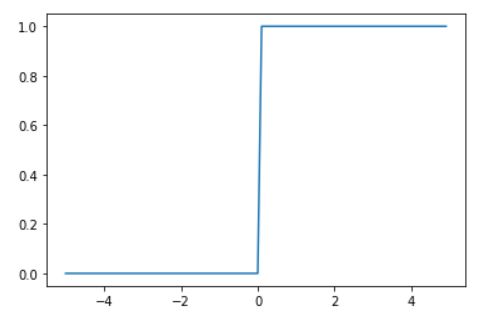
阶跃函数
感知机的输出基本上就采用阶跃函数,
如果输入的值小于等于零,则输出0,反之输出1
def step_function(x):
y = x>0
return y.astype(np.int)
x = np.array([-1,6.5,0])
step_function(x)
array([0, 1, 0])
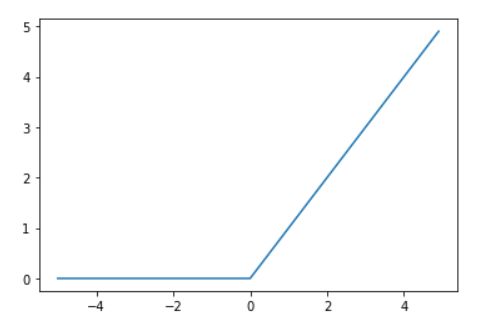
阶跃函数的图像
import matplotlib.pyplot as plt
x = np.arange(-5,5,0.1)
y = step_function(x)
plt.plot(x,y)
plt.show()
 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jFcWVgMY-1635647644774)(output_16_0.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jFcWVgMY-1635647644774)(output_16_0.png)]
激活函数
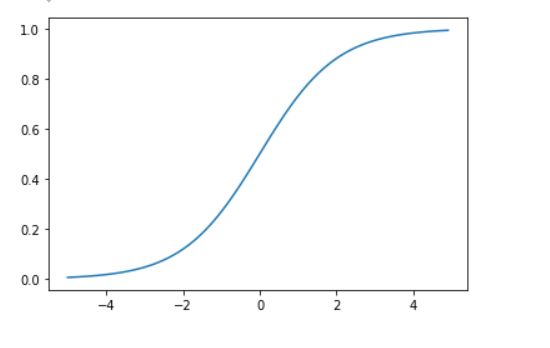
sigmoid函数
阶跃函数的形状非常有棱有角,然而sigmoid函数则是阶跃函数的平滑版本
其函数形式为:
g(z) = 1/(1+exp(-z))
def sigmoid(x):
return 1/(1+np.exp(-x))
import matplotlib.pyplot as plt
x = np.arange(-5,5,0.1)
y = sigmoid(x)
plt.plot(x,y)
plt.show()
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-mdQjeDlS-1635647644783)(output_18_0.png)]
ReLu函数
def ReLu(x):
return np.maximum(0,x) # 这里使用了numpy中的maximun函数,作用是取两个值中较大的那一个
import matplotlib.pyplot as plt
x = np.arange(-5,5,0.1)
y = ReLu(x)
plt.plot(x,y)
plt.show()
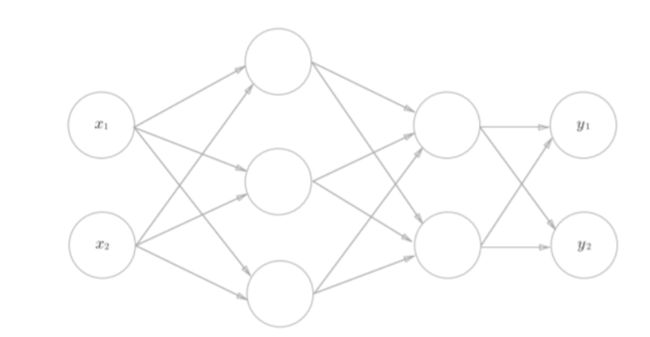
三层神经网络的实现
以这个神经网络结构为例
W1 为2*3形状的矩阵
W2 为 3*2形状的矩阵
W3 为2*2 形状的矩阵
def init_network(): #创建一个基本的神经网络结构
network = {}
network['W1'] = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
network['b1'] = np.array([0.1,0.2,0.3])
network['W2'] = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
network['b2'] = np.array([0.1,0.2])
network['W3'] = np.array([[0.1,0.3],[0.2,0.4]])
network['b3'] = np.array([0.1,0.2])
return network
def forword(network,x): # 向前传播算法
W1,W2,W3 = network['W1'],network['W2'],network['W3']
b1,b2,b3 = network['b1'],network['b2'],network['b3']
a1 = np.dot(x,W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1,W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2,W3) + b3
y = a3
return y
network = init_network()
x = np.array([1.0,0.5])
y = forword(network,x)
print(y) # [0.31682708 0.69627909]
softmax函数
在许多情况下,我们需要进行分类预测,通常来说,输出的值根据类别的多少,一般是一个长度为n的向量(n是类别的个数)
softmax函数的作用就是将原本神经网络输出的值通过一定运算,将其转换为该输入属于各个类别的可能性
def softmax(x):
x = np.exp(x)
exp_sum = np.sum(x)
x = x/exp_sum
return x
def softmax_pro(x):
x = x-np.max(x)
x = np.exp(x)
exp_sum = np.sum(x)
x = x/exp_sum
return x
这里我们用了两个softmax函数,第二个是对sotfmax函数进行了一定的优化,
由于指数函数的运算,计算出来的值经常会非常大,导致计算结果溢出,
而指数函数的指数加上一个数,就相当于指数函数在外边乘以一个数
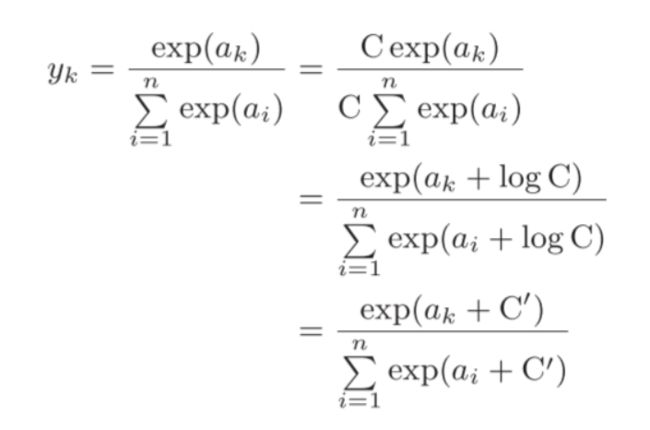
这样一来,只要我们对x的各个量进行相同的加减运算,是不影响结果的
为了尽量保证结果不溢出,我们将其减去其最大值
读取minist数据集
这里的mnist数据集是我事先下载好的,大家也可以在网上自行下载
from mnist import load_mnist(x_train,y_train),(x_test,y_test) = load_mnist(normalize =False ,flatten = True,one_hot_label = False)python
x_test.shape,y_test.shape
((10000, 784), (10000,))
显示第一张图片
from PIL import Image
def img_show(img):
pil_img = Image.fromarray(np.uint8(img))
pil_img.show()
img = x_test[0]
img = img.reshape(28,28)
label = y_test[0]
img_show(img)
print(label)
7
手写数字识别
import numpy as np
import sys,os,pickle
from sklearn.preprocessing import StandardScaler
sys.path.append(os.pardir)
from mnist import load_mnist
def get_data():
(x_train,t_train),(x_test,t_test) = load_mnist(normalize = True,flatten = True,one_hot_label = False)
return x_test,t_test
def init_network():
with open('sample_weight.pkl','rb') as f: # 这里我们暂且调用训练好了的模型来进行预测,
#在之后我们可以自己实现模型的训练
network = pickle.load(f)
return network
def predict(network,x):
W1,W2,W3 = network['W1'],network['W2'],network['W3']
b1,b2,b3 = network['b1'],network['b2'],network['b3']
a1 = np.dot(x,W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1,W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2,W3) + b3
y = softmax_pro(a3)
return y
x,t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(0,len(x)):
y = predict(network,x[i])
p = np.argmax(y)
if p == t[i]:
accuracy_cnt+=1
acc = accuracy_cnt/len(x)
print(str(acc)+'%')
0.9352%
这里的准确率有93%,但是其实并不算特别高
mini_batch
刚刚训练的时候,我们是一条数据一条数据进行运算的,
但是numpy里面对矩阵的运算进行了高度的优化,如果我们批量地进行矩阵运算,
可以将计算资源更多的集中在计算而不是数据的读取上
x_batch,t_batch = get_data()
network = init_network()
batch_size = 100
accurucy_cnt = 0
for i in range(0,len(x),batch_size):
x0 = x_batch[i:i+batch_size]
y = predict(network,x0)
p = np.argmax(y,axis = 1)
accurucy_cnt += np.sum(p==t[i:i+batch_size])
acc = accurucy_cnt/len(x_batch)
print(str(acc)+'%')
0.9352%
误差函数
交叉熵误差函数
def cross_entropy_error(y,t):
delta = 1e-7 # 为了避免出现log0的情况,给每个log都加上一个很小的值
if np.ndim(y) ==1:
y = y.reshape(1,y.size)
t = y.reshape(1,t.size)
batch_size = y.shape[0]
result = -np.sum(t*np.log(y+delta))/batch_size
return result
import numpy as np
import matplotlib.pyplot as plt
def numerical_diff(f,x): # 手动数值微分
h = 1e-4
return (f(x+h)-f(x-h))/(2*h)
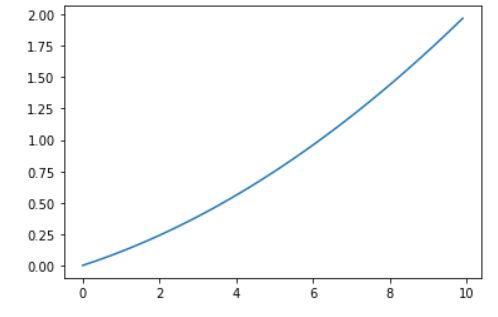
def function_1(x):
return 0.01*x**2+0.1*x
x = np.arange(0,10,0.1)
y = function_1(x)
plt.plot(x,y) # 画出函数曲线
[]
print(numerical_diff(function_1,5)) # 对函数进行求导
print(numerical_diff(function_1,10))
0.1999999999990898
0.2999999999986347
偏导的计算
我们经常遇到输入的值x是一个向量的情况,所以我们就需要计算偏导
我们先用定义来算一下偏导
然后根据算出来的偏导数,或者说是梯度,去进行梯度下降的运算
def numerical_gradient(f,x): # 实现向量x的各个偏导的计算
grad = np.zeros_like(x)
h=1e-4
for idx in range(x.size):
temp = x[idx] # 计算f(x+h)
x[idx] = temp + h
hx1 = f(x)
x[idx] = temp - h # 计算f(x-h)
hx2 = f(x)
x[idx] = temp
grad[idx] = (hx1-hx2)/(2*h)
return grad
def gradient_dicent(f,init_x,lr,step_num):
x = init_x
for i in range(step_num):
grad = numerical_gradient(f,x)
x-= lr*grad
return x
def function_2(x):
return x[0]**2+x[1]**2
x = np.array([-3.0,4.0])
print(gradient_dicent(function_2,x,0.1,100))
[-6.11110793e-10 8.14814391e-10]
实现一个简单的神经网络的类
class simple_net():
def __init__(self):
self.W = np.random.randn(2,3)
def predict(self,x):
return np.dot(x,self.W)
def loss(self,x,t):
z = self.predict(x)
y = softmax_pro(z)
loss = cross_entropy_error(y,t)
return loss
import sys,os
sys.path.append('your_path')
import numpy as np
from common.gradient import numerical_gradient # 这里的包是写好的,刚刚实现的略有不同
net = simple_net()
init_x = np.array([0.6,0.9])
z = net.predict(x) # 进行预测
print(z)
t = np.array([0,0,1])
net.loss(init_x,t) # 查看损失函数的值
def f_net(W):
return net.loss(init_x,t)
numerical_gradient(f_net,net.W)
array([[ 0.01116263, 0.07718392, -0.08834655],
[ 0.01674394, 0.11577588, -0.13251983]])
这里的f_net(W)只是为了和之前的形式统一起来,W这个参数并没有什么实际作用