【DL学习笔记02】深度学习入门——基于Python的理论与实现（ch03：Neural Network）

目录

1. Activation Function

step function

sigmoid function

ReLU

2. 多维数组的运算

多维数组

矩阵乘法

神经网络的内积

3. 三层神经网络的实现

问题

各层信号传递的实现

4. 输出层的设计

softmax

5. 手写数字识别

MNIST数据集

神经网络的推理处理

批处理（batch）

---

1. Activation Function

激活函数会将输入信号的总和转换为输出信号

• 朴素感知机是指单层网络，指的是激活函数使用了阶跃函数的模型
• 多层感知机是指神经网络，即使用sigmoid函数等平滑的激活函数的多层网络

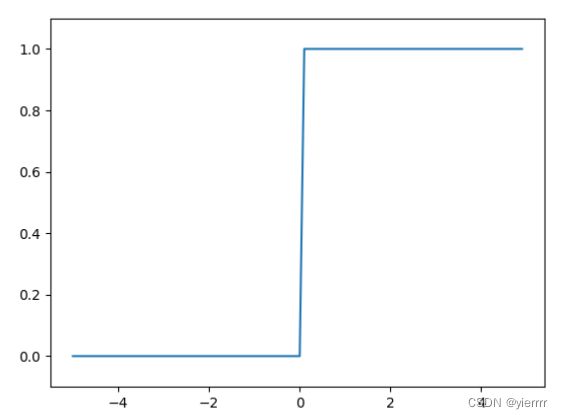
step function

阶跃函数：以阈值为界，一旦输入超过阈值，就切换输出

• 简单实现

  def step_function1(x):
      if x > 0:
          return 1
      else:
          return 0
  
  # 如上简单的实现不允许参数取NumPy数组，考虑下述实现
  def step_function2(x):
      y = x > 0
      return y.astype(np.int)
  
  # 再简化
  def step_function(x):
      return (x > 0).astype(np.int)
  

• 图形

  x = np.arange(-5.0, 5.0, 0.1)
  y = step_function(x)
  plt.plot(x, y)
  plt.ylim(-0.1, 1.1)  # 指定y轴的范围
  plt.show()
  

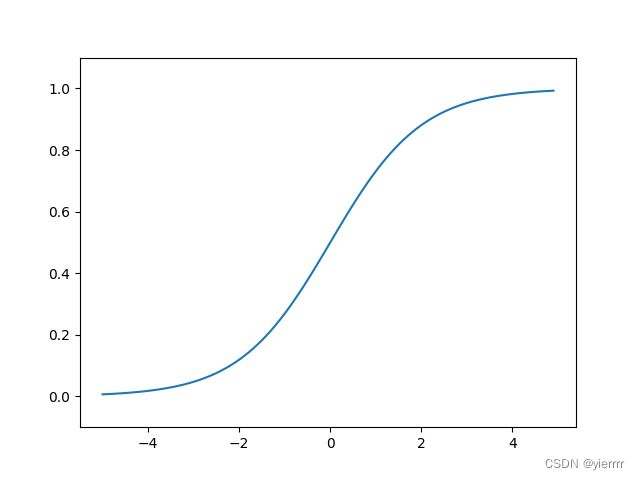
sigmoid function

• 实现

  def sigmoid(x):
      return 1 / (1 + np.exp(-x))
  

• 图形

  x = np.arange(-5.0, 5.0, 0.1)
  y = sigmoid(x)
  plt.plot(x, y)
  plt.ylim(-0.1, 1.1)  # 指定y轴的范围
  plt.show()
  

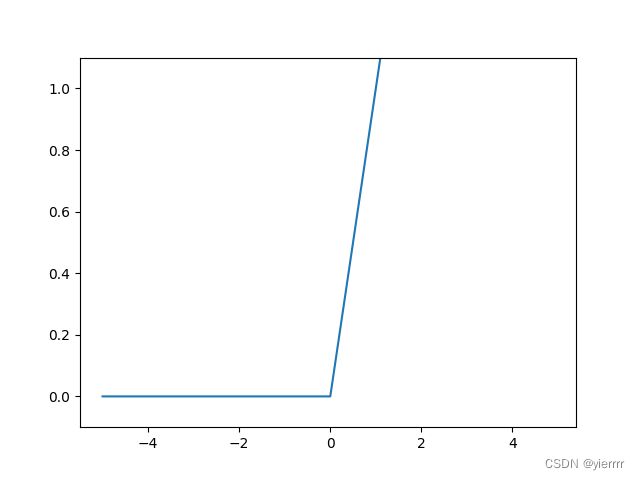
ReLU

• 实现

  def relu(x):
      return np.maximum(0, x)
  

• 图形

  x = np.arange(-5.0, 5.0, 0.1)
  y = relu(x)
  plt.plot(x, y)
  plt.ylim(-0.1, 1.1)  # 指定y轴的范围
  plt.show()
  

2. 多维数组的运算

多维数组

# 一维数组
>>>A = np.array([1, 2, 3, 4])
>>>print(A)
[1 2 3 4]
>>>np.ndim(A)  # 获取数组的维数
1
>>>A.shape  # 获取数组的形状，返回结果是一个元组
(4,)
>>>A.shape[0]  # 获取指定内容
4

# 二维数组
>>>B = np.array([[1, 2], [3, 4], [5, 6]])
>>>print(B)
[[1 2]
 [3 4]
 [5 6]]
>>>np.ndim(B)
2
>>>B.shape
(3, 2)

矩阵乘法

• 使用np.dot(a, b, out=type)函数

>>>A = np.array([[1, 2], [3, 4]])
>>>A.shape
(2, 2)
>>>B = np.array([[5, 6], [7, 8]])
>>>B.shape
(2, 2)
>>>np.dot(A, B)
array([[19, 22],
       [43, 50]])

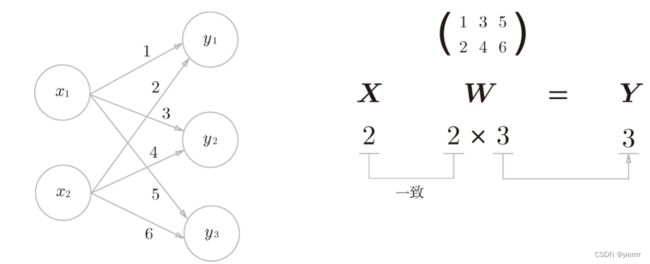
神经网络的内积

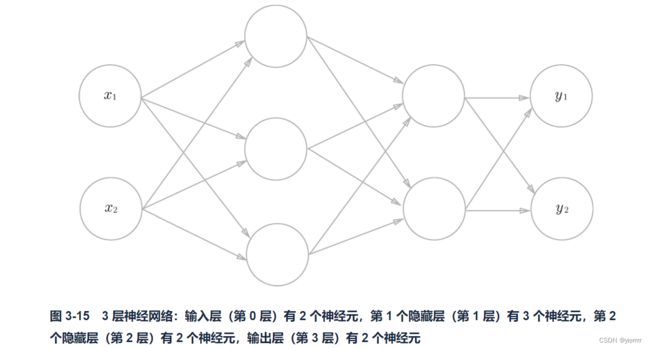
3. 三层神经网络的实现

问题

 

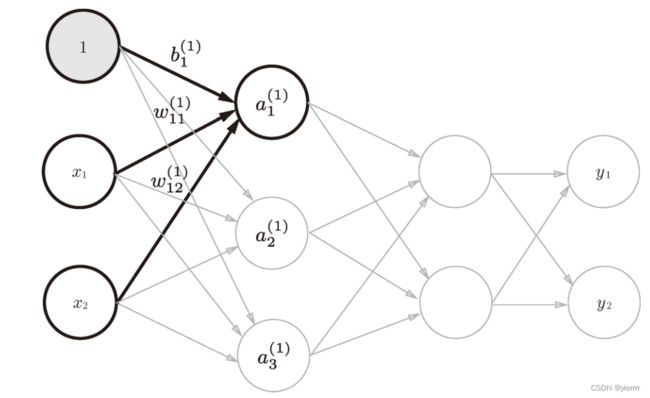
各层信号传递的实现

# 从输入层到第1层
X = np.array([1.0, 0.5])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.3])
A1 = np.dot(X, W1) + B1
# 使用sigmoid函数
Z1 = sigmoid(A1)

# 从第1层到第2层
W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
B2 = np.array([0.1, 0.2])
A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)

# 第2层到输出层
# 输出层的激活函数用σ（）表示
# 一般的，回归问题用恒等函数，二元分类用sigmoid函数，多元分类用softmax函数
# 恒等函数：将输入按原样输出
def identity_function(x):
    return x

W3 = np.array([[0.1, 0.3], [0.2, 0.4]])
B3 = np.array([0.1, 0.2])
A3 = np.dot(Z2, W3) + B3
Y = identity_function(A3)

• 代码结构优化

  import numpy as np
  
  # 进行权重和偏置的初始化，并将它们保存在字典变量network中
  # 该字典变量中保存了每一层所需的参数（权重和偏置）
  from torch import softmax
  
  from ch3_NeuralNetworks.SigmoidFunction import sigmoid
  from ch3_NeuralNetworks.three_layer_NN1 import identity_function
  
  def init_network():
      network = {}
      network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
      network['b1'] = np.array([0.1, 0.2, 0.3])
      network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
      network['b2'] = np.array([0.1, 0.2])
      network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
      network['b3'] = np.array([0.1, 0.2])
  
      return network
  
  def forward(network, x):
      W1, W2, W3 = network['W1'], network['W2'], network['W3']
      b1, b2, b3 = network['b1'], network['b2'], network['b3']
  
      a1 = np.dot(x, W1) + b1
      z1 = sigmoid(a1)
      a2 = np.dot(z1, W2) + b2
      z2 = sigmoid(a2)
      a3 = np.dot(z2, W3) + b3
      y = identity_function(a3)
  
      return y
  
  network = init_network()
  x = np.array([1.0, 0.5])
  y = forward(network, x)
  print(y)
  

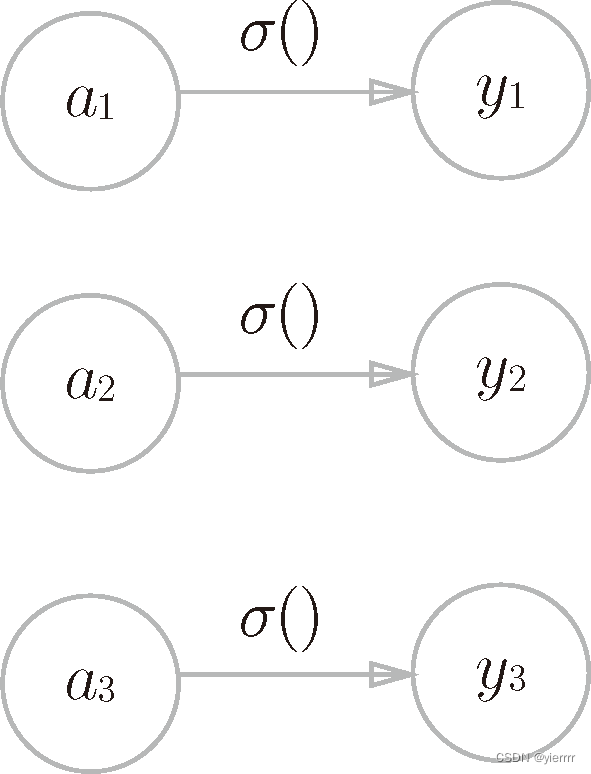
4. 输出层的设计

神经网络可以用在分类问题和回归问题上，不过需要根据情况改变输出层的激活函数。一般而言，回归问题用恒等函数，分类问题用softmax函数

• 恒等函数

• softmax函数

 

softmax

import numpy as np

def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a - c)  # 溢出对策
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a

    return y

• 函数输出的是0.0到1.0之间的实数
• 函数输出值的总和是1，因此可以将输出解释为“概率”
• 即使使用了softmax函数，各个元素之间的大小关系也不会改变
  • 因为指数函数是单调递增函数
  • 神经网络只把输出值最大的神经元所对应的类别作为识别结果
  • 因此神经网络在进行分类时，输出层的softmax函数可以省略

5. 手写数字识别

• 机器学习求解步骤分为“学习”和“推理”两个阶段
  • 学习阶段进行模型的学习（训练）
  • 推理阶段，用学到的模型对未知的数据进行推理（分类）
• 用神经网络解决问题的步骤和上面一样
  • 首先使用训练数据（学习数据）进行权重参数的学习
  • 进行推理时，使用刚才学到的参数，对输入数据进行分类

MNIST数据集

import sys
import os
import numpy as np
from PIL import Image
sys.path.append(os.pardir)
from mnist import load_mnist

# 载入数据集
# (训练图象，训练标签)，(测试图象，测试标签)
# flatten : 是否将图像展开为一维数组
# normalize : 将图像的像素值正规化为0.0~1.0，否则保持0~255
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)

# 输出各个数据的形状
print(x_train.shape, t_train.shape, x_test.shape, t_test.shape)

# 显示第一张图片
def img_show(img):
    pil_img = Image.fromarray(np.uint8(img))
    pil_img.show()

img = x_train[0]
label = t_train[0]
print(label)
print(img.shape)
img = img.reshape(28, 28)  # 把图象的形状变成原来的尺寸
print(img.shape)
img_show(img)

神经网络的推理处理

• 输入层有784个神经元（图像大小为28*28）

• 输出层有10个神经元（数字0-9）

• 有两个隐藏层，第一个隐藏层有50个神经元，第二个隐藏层有100个神经元（可以为任意值）

• 用以下3个函数来实现神经网络的推断处理(假设上述学习已完成)

  • get_data()

    def get_data():
        (x_train, t_train), (x_test, t_test) = \\
            load_mnist(flatten=True, normalize=False, one_hot_label=False)
        return x_test, t_test
    

  • init_network()

    def init_network():
        with open("sample_weight.pkl", 'rb') as f:
            network = pickle.load(f)
    
        return network
    

  • predict()

    def predict(network, x):
        W1, W2, W3 = network['W1'], network['W2'], network['W3']
        b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        z2 = sigmoid(a2)
        a3 = np.dot(z2, W3) + b3
        y = softmax(a3)
    
        return y
    

• 识别精度：即能在多大程度上正确分类

  # 首先获得MNIST数据集，然后生成网络
  x, t = get_data()
  network = init_network()
  # 用for语句逐一取出保存在x中的图像数据，用predict进行分类
  accuracy_cnt = 0
  for i in range(len(x)):
      y = predict(network, x[i])
      p = np.argmax(y)
      if p == t[i]:
          accuracy_cnt += 1
  
  print("Accuracy:" + str(float(accuracy_cnt) / len(x)))
  

• 正规化（normalization）：把数据限定到某个范围内的处理

  • 上述有：load_mnist()函数中，当参数normalize设置为True时，会将图像的各个像素值除以255，使得数据的值在0.0~1.0的范围内。

• 预处理（pre-processing）：对神经网络的输入数据进行某种既定的转换

批处理（batch）

打包式输入数据称为批（batch）

• 批处理对计算机的运算大有利处

# 加粗部分是与之前的实现的不同之处
x, t = get_data()
network = init_network()

**# 一次输入100个数据**
**batch_size = 100  # 批数量**
accuracy_cnt = 0
**# i=0，100，200......**
**for i in range(0, len(x), batch_size):
		# 切片取出批数据
    x_batch = x[i:i+batch_size]
    y_batch = predict(network, x_batch)
		# 给定参数axis=1，表示指定在y_batch这个100*10的数组中
		# 沿第1维方向找到值最大的元素的索引（第0维为列方向，第1维为行方向）
    p = np.argmax(y_batch, axis=1)
		# ‘p == t[i:i+batch_size]’ 得到一个布尔型数组，通过sum()得到值为True的个数
    accuracy_cnt += np.sum(p == t[i:i+batch_size])**

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))