第一章 | 加州房价数据集 | 端到端的机器学习 | 回归问题 | tensorflow2.6+sklearn | 学习笔记

1. 实验目标

选择加州房价数据集，基于1990年加州人口普查的数据，出于教学的目的，添加了一个分类属性，并且移除了一些特征。
模型需要从这个数据中学习，从而能够根据所有其他指标，预测任意区域的房价中位数

2. 数据集展示

housing.info()

# 存在缺失值,将在 5.3 中进行处理

RangeIndex: 20640 entries, 0 to 20639
Data columns (total 10 columns):
longitude             20640 non-null float64                 #  位置
latitude              20640 non-null float64                 #  位置
housing_median_age    20640 non-null float64                 # 房龄
total_rooms           20640 non-null float64              # 总房数
total_bedrooms        20433 non-null float64			  # 总卧室数
population            20640 non-null float64				# 总人口
households            20640 non-null float64				# 家庭数
median_income         20640 non-null float64		    # 收入中位数
median_house_value    20640 non-null float64		# 房价中位数
ocean_proximity       20640 non-null object			# 离海距离

3. 设计系统

1. 首先，我们需要回答框架问题：监督式，还是无监督式，又或者强化学习。是分类任务，还是回归任务，又或者是其他任务。应该采用批量学习还是在线学习技术？
2. 显然，这是一个典型的监督学习任务，因为已经给出了标记的训练示例(每个示例都有预期的产出，也就是该地区的房价中位数)
3. 并且，这也是一个典型的回归任务，因为需要对某个值进行预测。更具体而言，这是一个多变量回归问题，因为系统需要使用多个特征进行预测。
4. 最后，我们没有一个连续的数据流不断的流进系统，所以不需要针对数据做出特别的调整，数据量也不是很大，不需要多个内存，故简单的批量学习就能胜任

4. 探索数据

绘制每个特征的直方图：

import matplotlib.pyplot as plt
housing.hist(bins=50,figsize=(20,15),edgecolor="black")
plt.show()

观察直方图，可以发现：

1. 收入中位数这个属性看起来不像是用美元(USD)在衡量。通过核实，得知数据已经按比例缩小，并框处中位数的上限为15，下限为0.5.在机器学习中，使用经过预处理的属性是很常见的事情，倒不一定是个问题，但是至少要了解数据是如何计算的。

2. 房龄中位数和房价中位数也被设定了上限，而后者正是我们需要的目标属性(标签),这是个问题，因为这样机器学习算法很可能永远也学不到超过这个上限的价格。因此，需要继续和客户进行核实，查看是否存在问题。如果他们说，需要精确的预测值，甚至会超过50w美元。那么，我们通常有两个选择：
   （1）对被设置了上限的区域，重新收集标签值。
   （2）或是将这些区域的数据从训练集中移除(包括从测试中移除，因为如果预测值超过50w,系统表现会比较差)

3. 最后，很多直方图都表现出重尾：图形在中位数右侧会比左侧要远得多。
   这可能会导致某些机器学习算法难以检测模式。稍后我们会尝试一些转化方法，将这些属性转化为更偏向于钟形的分布(正态分布的一种)

5. 代码部分

5.1 划分数据集

我们可以直接用 sklearn 中的 train_test_split

from sklearn.model_selection import train_test_split
train_set,test_set=train_test_split(housing,test_size=0.2,random_state=42)
print(len(train_set),"train+",len(test_set),"test")
>> 16512 train+ 4128 test

但是使用上面的方法,对于这样的随机在面对小样本时,容易出现抽样偏差，
因此需要考虑分层抽样
使用StratifiedShuffleSplit,以median_income为依据进行分层抽样,因为median_income图像看起来更规则,符合钟形分布,并且,人群收入特征对于区域房价具有重要意义.

housing["median_income"].hist(edgecolor="black")

我们尽量使抽取的数据符合钟形分布（正态分布的一种形式），因为钟形分布的数据更容易拟合数据集，增加模型的泛化能力。

housing["income_cat"] = pd.cut(housing["median_income"],
                               bins=[0., 1.5, 3.0, 4.5, 6., np.inf], 
                               labels=[1, 2, 3, 4, 5])
housing["income_cat"].hist(edgecolor="black")

按收入比例进行分层抽样

# 关于StratifiedShuffleSplit可自行百度
from sklearn.model_selection import StratifiedShuffleSplit
# n_splits比例范围内的划分为1组
ss=StratifiedShuffleSplit(n_splits=1,test_size=0.2,random_state=42)
for train_index,test_index in ss.split(housing,housing["income_cat"]):
    strat_train_set=housing.loc[train_index]
    strat_test_set=housing.loc[test_index]
    print(len(strat_train_set),len(strat_test_set))

验证一下分层抽样后的训练集和测试集结果

strat_train_set["income_cat"].value_counts()/len(strat_train_set)
strat_test_set["income_cat"].value_counts()/len(strat_test_set)
>>
3    0.350533
2    0.318798
4    0.176357
5    0.114583
1    0.039729
Name: income_cat, dtype: float64

删除income_cat属性

strat_train_set.drop('income_cat',axis=1,inplace=True)  
strat_test_set.drop('income_cat',axis=1,inplace=True)

5.2 探索训练集

接下来我们把测试集扔一边，探索一下训练集
housing=strat_train_set.copy()

# 带上地图
import matplotlib.image as mpimg
california_img=mpimg.imread('./images/end_to_end_project/california.png')
ax = housing.plot(kind="scatter", x="longitude", y="latitude", figsize=(10,7),
                       s=housing['population']/100, label="Population",
                       c="median_house_value", cmap=plt.get_cmap("jet"),
                       colorbar=False, alpha=0.4,
                      )
plt.imshow(california_img, extent=[-124.55, -113.80, 32.45, 42.05], alpha=0.5,
           cmap=plt.get_cmap("jet"))
plt.ylabel("Latitude", fontsize=14)
plt.xlabel("Longitude", fontsize=14)

prices = housing["median_house_value"]
tick_values = np.linspace(prices.min(), prices.max(), 11)
cbar = plt.colorbar()
cbar.ax.set_yticklabels(["$%dk"%(round(v/1000)) for v in tick_values], fontsize=14)
cbar.set_label('Median House Value', fontsize=16)

plt.legend(fontsize=16)
plt.show()

从这张图片可以看出,靠海的,人口密度大的房子价格就高,反之则不同
如果画图比较麻烦,这里我们可以pass这一步,直接转入下一步,这里只是为了让我们了解训练集,对我们的后续操作没有太大影响.

使用 corr() 在数据集上计算目标值对属性间的标准相关系数（也称为皮尔逊相关系数）
越接近1和-1 越相关，0代表没有线性关系
注意:只能测量线性相关性,会遗漏非线性相关性

corr_matrix=housing.corr()
# median_house_value 目标值
corr_matrix["median_house_value"].sort_values(ascending=False)
>>
median_house_value    1.000000
median_income         0.687160
total_rooms           0.135097
housing_median_age    0.114110
households            0.064506
total_bedrooms        0.047689
population           -0.026920
longitude            -0.047432
latitude             -0.142724
Name: median_house_value, dtype: float64

以上可以看出:
1. 收入跟房价成正相关,是非常重要的特征
2. households, total_bedrooms,population,longitude这几个特征对于目标值来说,是没有多大相关性的
3. 可以尝试组合新的属性,看看对目标值的影响

根据目前信息创造有更大价值的特征数据
比如:

1. 如果不知道一个地区有多少个家庭，那么知道一个地区的“总房屋数”也没什么。我们真正想知道的是每个家庭的房屋数量。
2. 同样，但看“卧室总数”这个属性本身，也没有什么意义，我们可能是想拿它和“房屋总数”来对比，或者每个家庭的人口数这个属性结合也似乎挺有意思。
3. 或许还可以组合成每个房屋的卧室数,也是日常生活中,衡量房价的重要指标

# 创造以上所说的三个特征
housing["rooms_per_household"] = housing["total_rooms"]/housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"]
housing["population_per_household"]=housing["population"]/housing["households"]

# 查看新特征与目标值的相关系数
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)
>>
median_house_value          1.000000
median_income               0.687160
rooms_per_household         0.146285
total_rooms                 0.135097
housing_median_age          0.114110
households                  0.064506
total_bedrooms              0.047689
population_per_household   -0.021985
population                 -0.026920
longitude                  -0.047432
latitude                   -0.142724
bedrooms_per_room          -0.259984
Name: median_house_value, dtype: float64

新的特征,相较于“房屋总数”还是“卧室总数”与房价中位数的相关性都要高得多。显然卧室/房屋比例更低的房屋，往往价格越贵。
同样“每一个家庭的房间数量”也比“房间总数”更具信息量–房屋越大，价格越贵.

分离训练集和目标集

housing_train = strat_train_set.drop('median_house_value',axis=1)
housing_label = strat_train_set['median_house_value'].copy()

5.3 特征工程

5.3.1 数值类型处理

大部分机器学习算法无法在缺失的特征上工作,所以我们要创建一些函数来辅助它。 前面我们已经注意到total_bedrooms属性有部分值缺失，所以需要解决。 有以下三种选择:

1. 放弃这些相应的地区
2. 放弃这个属性
3. 将缺失值设置为某个值

方法一,删除空值对应的信息

sample_incomplete_rows.dropna(subset=["total_bedrooms"])  

方法二,放弃该属性

sample_incomplete_rows.drop("total_bedrooms", axis=1)

方法三，用中位数填充

median = housing["total_bedrooms"].median()
sample_incomplete_rows["total_bedrooms"].fillna(median, inplace=True) 

这里 我们选择方法三

使用sklearn中的SimpleImputer函数来实现,该函数只能处理纯数值型的dataframe

# 删除文本型的特征
housing_num = housing_train.drop('ocean_proximity', axis=1)

imputer = SimpleImputer(strategy='median')

# 这里fit属于估算器，transform属于转换器，fit_transform是两者结合，进行优化后的
X = imputer.fit_transform(housing_num)
housing_tr = pd.DataFrame(X,columns=housing_num.columns,index=housing_num.index)

5.3.2 文本类型处理

文本属性 分类属性
这里有个注意点，下方代码的取值:
1.如果是[]，那么housing_cat.value是1维的
2.如果是[[ ]] 那么housing_cat.value是2维的
类别转化需要2维d数据,所以使用第2种取值方式

housing_cat = housing_train[['ocean_proximity']]

将文本属性进行数字化编码
使用sklearn中的OrdinalEncoder

# 处理分类文本属性
from sklearn.preprocessing import OrdinalEncoder

ordinal_encoder = OrdinalEncoder()
housing_cat_encoded = ordinal_encoder.fit_transform(housing_cat)
print(housing_cat_encoded[:10])
# 获取他的索引和类别
for index,cate in enumerate(ordinal_encoder.categories_[0]):
    print(index,cate)

将文本属性转化为稀疏矩阵
稀疏矩阵: one_hot编码后只记住1的位置，提高运算效率

cat_encoder = OneHotEncoder()
housing_cat_one_hot = cat_encoder.fit_transform(housing_cat)
print(cat_encoder.categories_)
print(housing_cat_one_hot.toarray())

5.3.3 sklearn数值流水线处理

自定义转换器,添加5.2中的说明的新属性,使用sklearn封装,方便测试集调用流水线处理

from sklearn.base import BaseEstimator,TransformerMixin

# 
rooms_id,bedrooms_id,population_id,households_id = 3,4,5,6
class CombineAttributesAdder(BaseEstimator,TransformerMixin):
    def __init__(self,add_bedrooms_per_room=True):
        self.add_bedrooms_per_room = add_bedrooms_per_room
    def fit(self,X,y=None):
        return self
    def transform(self,X):
        rooms_per_household = X[:,rooms_id]/X[:,households_id]
        population_per_household = X[:,population_id]/X[:,households_id]
        if self.add_bedrooms_per_room:
            bedrooms_per_room = X[:,bedrooms_id]/X[:,rooms_id]
            return np.c_[X,rooms_per_household,population_per_household,bedrooms_per_room]
        else:
            return np.c_[X, rooms_per_household, population_per_household]

np.c_ 按行连接,矩阵左右相加,要求行数相同
np.r_ 按列连接,矩阵上下相加,要求列数相同

attr_adder = CombineAttributesAdder(add_bedrooms_per_room=False)
housing_extra_attr = attr_adder.transform(housing_train.values)

让我们来查看一下属性是否添加成功

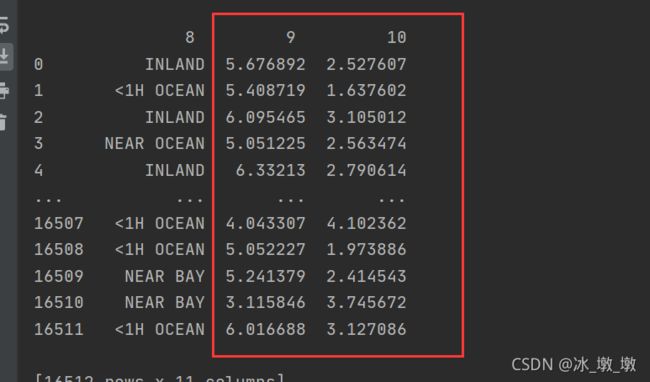
最后两列添加了rooms_per_household, population_per_household这两个属性,如果想要添加bedrooms_per_room属性,需要如下

attr_adder = CombineAttributesAdder(add_bedrooms_per_room=True)

经过以上实验,我们可以综合使用流水线进行处理,简化代码,一目了然

sklearn 流水线 pipline
Pipline 构造函数会定义步骤的顺序，除了最后一个可以是估算器之外，其他的必须是转换器，也就是说必须有fit_transform方法

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
num_pipline = Pipeline([
    ('imputer',SimpleImputer(strategy='median')),  # 使用中位数补充缺失值
    ('attr_adder',CombineAttributesAdder()),   # 添加额外的数值属性
    ('std_scaler',StandardScaler())        # 将数值属性标准化
])

流水线的方法与最终估算器的方法相同，因此这个流水线有transform方法

housing_num_str = num_pipline.fit_transform(housing_num)

查看一下是否按照我们代码正确执行
这里处理的是housing_num,剩下0-7共8个属性,而CombineAttributesAdder默认add_bedrooms_per_room=True,即添加之前提到过的三个新属性,所以,数值型的数据会出现0-10共11个属性,并且会进行按照流水线进行标准化

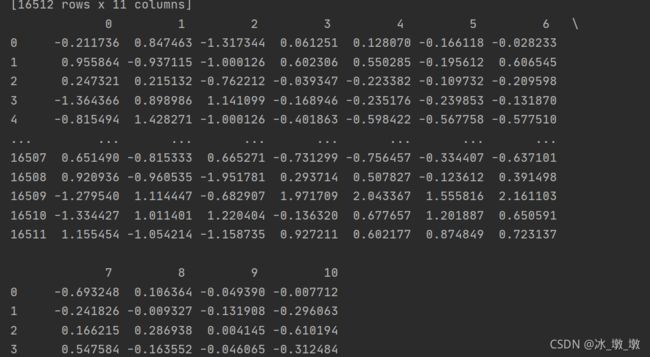
以上是数值处理的流水线
接下来合并处理文本类型的数据

# ColumnTransformer 返回一个密集矩阵或者是稀疏矩阵
# 默认情况下，未指定的列将会被删除
from sklearn.compose import ColumnTransformer

# list(housing_num)返回的是list类型的列名
num_attribs = list(housing_num)
cat_attribs = ['ocean_proximity']
full_pipeline = ColumnTransformer([
    ("num",num_pipline,num_attribs),    # 密集矩阵   num_pipline 是上面提到的代码
    ("cat",OneHotEncoder(),cat_attribs) # 稀疏矩阵   文本类型的one_hot处理
])

查看结果

housing_prepare = full_pipeline.fit_transform(housing_train)
print(pd.DataFrame(housing_prepare))

至此,文本数值类型均处理完毕,可以代入模型进行预测分析

5.4 模型部分

5.4.1 sklearn模型的保存和加载

import joblib
保存模型
# save model
joblib.dump(model,"house_model.pkl")
加载模型
# load model
model_loaded = joblib.load("my_model.pkl")

5.4.2 建立决策树和线性回归模型

回归模型的评价指标:
mean_absolute_error：平均绝对误差(Mean Absolute Error，MAE)，用于评估预测结果和真实数据集的接近程度的程度，其值越小说明拟合效果越好。

mean_squared_error：均方差(Mean squared error，MSE)，该指标计算的是拟合数据和原始数据对应样本点的误差的平方和的均值，其值越小说明拟合效果越好。

关于评价回归模型的这些详解可查:
https://www.jianshu.com/p/9ee85fdad150

下面建立模型并训练:

线性回归模型
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(housing_prepare,housing_label)

决策树模型
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor()
tree_reg.fit(housing_prepare, housing_label)

模型预测代码:

def lin_predict():
    some_data = housing_train.iloc[:5]  #取出训练集的前5行
    some_lable = housing_label.iloc[:5]
    some_data_prepare = full_pipeline.transform(some_data)  # 前面fit过了，不需要再加fit
    some_data_prediction = lin_reg.predict(some_data_prepare)
    print(some_data_prediction)
    print(some_lable.values)

到这一步,预测房价功能基本实现,效果还可以~~~~~

接下来调整模型,计算RMSE,尽可能找到更好的模型
计算两个模型的RMSE:

def lin_ca():  #68305.637
    housing_prediction = lin_reg.predict(housing_prepare)
    lin_mse = mean_squared_error(housing_label,housing_prediction)
    lin_rmse = np.sqrt(lin_mse)
    print(lin_rmse)

def tree_ca():
    tree_prediction = tree_reg.predict(housing_prepare)
    tree_mse = mean_squared_error(housing_label,tree_prediction)
    tree_rmse = np.sqrt(tree_mse)
    print(tree_rmse)

这里居然出现了0,我们可以看见，误差为0，这可能吗？是模型完美？还是严重过度拟合了？前面有提到，当我们有信心启动模型之前，都不要触碰测试集，所以这里，我们需要那训练集中的一部分用于训练，另一部分用来做模型验证.

5.4.3 使用交叉验证评估模型

# 交叉验证
from sklearn.model_selection import cross_val_score

# 利用交叉验证计算误差
def calcu_score():
    # sklearn 交叉验证功能更倾向于效用函数（越大越好）,而不是成本函数（越小越好），计算出来的分数实际上是一个负的MSE
    scores = cross_val_score(tree_reg,housing_prepare,housing_label,scoring='neg_mean_squared_error',cv=10)
    tree_rmse_scores = np.sqrt(-scores)
    display_score(tree_rmse_scores)

    print('-'*100)
    lin_scores = cross_val_score(lin_reg,housing_prepare,housing_label,scoring='neg_mean_squared_error',cv=10)
    lin_rmse_scores = np.sqrt(-lin_scores)
    display_score(lin_rmse_scores)

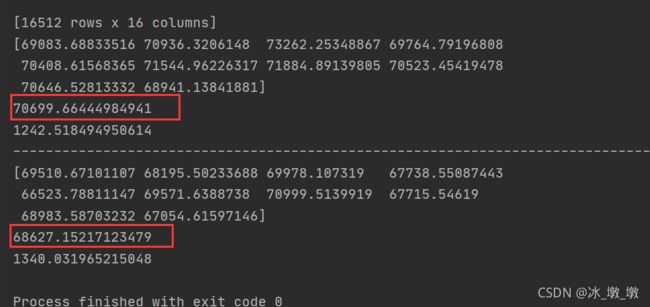
我们可以看见，线性回归模型的评分为68627，比决策树70699要稍微好点。

5.4.4 建立随机森林模型

接下来，我们尝试随机森林模型，以后会介绍随机森林的工作原理，通过对特征的随机子集进行多个决策树的训练，然后对其预测取平均值。
在多个模型的基础上建立模型，称为集成算法，这是进一步推动机器学习算法的好方法。

def random_forest():
    # 随机森林 对特征的随机子集进行许多决策树的训练，是在多个模型基础之上建立的模型，称为集成学习
    from sklearn.ensemble import RandomForestRegressor
    forest_reg = RandomForestRegressor()
    forest_reg.fit(housing_prepare,housing_label)
    forest_prediction = forest_reg.predict(housing_prepare)
    forest_mse = mean_squared_error(housing_label,forest_prediction)
    forest_rmse = np.sqrt(forest_mse)
    print(forest_rmse)

    forest_score = cross_val_score(forest_reg,housing_prepare,housing_label,scoring='neg_mean_squared_error',cv=10)
    forest_rmse_scores = np.sqrt(-forest_score)
    display_score(forest_rmse_scores)

我们可以看见效果要比前面两个都要好，但是训练集的评分仍然远低于验证集，这意味着模型仍然对训练集过度拟合

5.4.5 建立支持向量机SVR模型

# 尝试支持向量回归模型
from sklearn.svm import SVR

svm_reg = SVR(kernel="linear")
svm_reg.fit(housing_prepared, housing_labels)
housing_predictions = svm_reg.predict(housing_prepared)
svm_mse = mean_squared_error(housing_labels, housing_predictions)
svm_rmse = np.sqrt(svm_mse)
svm_rmse

这里的RMSE达到了111094,好吧,那我们就不继续尝试了,效果太差.
综上所述,我们找到了效果最好的就是随机森林的模型

5.4.6 网格搜索寻找最佳参数组合

要了解随机森林模型的几个重要超参数
n_estimators 集成的估算器数量
max_depth 最大树深度
n_jobs 使用多少cpu训练
max_features 划分时考虑的最大特征数
等等等等,这里可以自行查看手册

    from sklearn.model_selection import GridSearchCV
    from sklearn.ensemble import RandomForestRegressor
    param_grid = [
        {'n_estimators':[3,10,30],'max_features':[2,4,6,8]},
        {'bootstrap':[False],'n_estimators':[3,10],'max_features':[2,3,4]}
    ]

    # 先是3*4=12 + 2*3=6    18*5=90次计算
    forest_reg = RandomForestRegressor()   # refit=True 一旦找到了最佳估算器，那么就会在整个训练集上重新训练
    grid_sear = GridSearchCV(forest_reg,param_grid=param_grid,cv=5,scoring='neg_mean_squared_error',
                             return_train_score = True)
    grid_sear.fit(housing_prepare,housing_label)
    # 最佳参数组合
    print(grid_sear.best_params_)
    # 最好的估算器  对应的参数
    print(grid_sear.best_estimator_)

	# 显示测试平均得分和对应的使用参数
    cvres = grid_sear.cv_results_
    for mean_score,params in zip(cvres["mean_test_score"],cvres["params"]):
        print(np.sqrt(-mean_score),params)

    # 分析每个属性（列）的重要程度
    feature_importances = grid_sear.best_estimator_.feature_importances_
    # print(feature_importances)

    # 添加列名
    extra_attribs = ['rooms_per_hhold','pop_per_hhold','bedrooms_per_room']
    cat_encoder_ = full_pipeline.named_transformers_["cat"]
    cat_one_hot_attribs = list(cat_encoder_.categories_[0])  # ['<1H OCEAN', 'INLAND', 'ISLAND', 'NEAR BAY', 'NEAR OCEAN']
    # 原来的训练集数值的标签   额外的三个标签   文本格式的标签
    attributes = num_attribs+extra_attribs+cat_one_hot_attribs
    # 通过输出结果，可以删除一些不怎么有用的特征
    print(sorted(zip(feature_importances,attributes),reverse=True))

    print("-"*100 +"华丽的分割线"+"-"*100)

5.5 通过测试集评估系统

使用经过网格搜索出来的最好的模型
作为最终测试模型

    final_model = grid_sear.best_estimator_

    X_test = strat_test_set.drop("median_house_value",axis=1)
    y_test = strat_test_set['median_house_value'].copy()

    # 这里在之前已经fit过了，不要重新fit拟合
    X_test_prepare = full_pipeline.transform(X_test)
    final_predictions = final_model.predict(X_test_prepare)

    final_mse = mean_squared_error(y_test,final_predictions)
    final_rmse = np.sqrt(final_mse)

    # rmse是泛化误差，估计的精确度可以使用scipy计算置信区间
    from scipy import stats
    confidence = 0.95
    squared_errors = (final_predictions-y_test)**2
    num = np.sqrt(stats.t.interval(confidence,len(squared_errors)-1,
                             loc=squared_errors.mean(),
                             scale = stats.sem(squared_errors)))
    print(num)

6. 建议

一般而言，这个结果会略逊于之前使用交叉验证的表现结果(因为用过不断调整，系统虽然在验证数据上终于表现良好，在未知数据上可能达不到那么好的效果)。在本例中，虽然并非如此，但是如果效果不好，不要忍不住去调超参数，不要试图再努力让测试集的结果也变得好看一些，因为这些改进会在泛化到新的数据集时，又变成徒劳。
现在进入项目预启动阶段：

展示解决方案(强调学习了什么，什么有用，什么没有用，基于什么假设，以及系统的限制有哪些)
记录所有事情
通过清晰的可视化和易于记忆的陈述方式，制作漂亮的演示文稿(例如：收入中位数是预测房价的首要指标)

6.1 启动、监控和维护系统

1.为生产环境做好准备，特别是将生产数据源接入系统，并编写测试。
2.编写监控代码，定期检查系统实时性能，在性能下降的时候触发警报
3.评估系统性能，对系统的预测结果进行抽样评估，这一步一般需要人工分析
4.需要评估输入系统的数据的质量
5.使用新鲜数据定期训练模型，这个过程要尽可能自动化

6.2 最后

通过本章内容，希望能让读者了解一个机器学习项目大概是什么样子，同时本章也提供了一些用来训练系统的工具，如你所见，大部分工作主要在数据准备，构建监控工具，建立人工评估的流水线以及自动定期训练模型上、
机器学习算法固然重要，但是最好还是对整个流程都熟悉一遍，掌握3-4个合适的算法，不要将所有的时间都用来探索高级的算法，而对整个流程视而不见。
kaggle是一个不错的起点