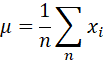pytorch 层标准化 LayerNorm 的用法

目录

1、为什么要标准化（理解的直接跳过到这部分）

2、LayerNorm 解释

3、举例-只对最后 1 个维度进行标准化

4、举例-对最后 D 个维度进行标准化

---

1、为什么要标准化（理解的直接跳过到这部分）

Batch Normalization 的作用就是把神经元在经过非线性函数映射后向取值区间极限饱和区靠拢的输入分布强行拉回到均值为 0 方差为 1 的比较标准的正态分布的区间，使得非线性变换函数的输入值落入激活函数比较敏感的区域，这样会让让梯度变大，由此避免了梯度消失的问题。而梯度变大也意味着学习收敛速度快，能大大加快训练速度。

BN 的计算过程如下：

1、计算均值

2、计算方差

3、标准化：减均值后除以标准差（注意是标准差，不是方差）

4、仿射变换

使用 netron 工具可视化 LayerNorm 层的计算流图如下：

2、LayerNorm 解释

LayerNorm 是一个类，用来实现对 tensor 的层标准化，实例化时定义如下：

LayerNorm(normalized_shape, eps = 1e-5, elementwise_affine = True, device=None, dtype=None)

以一个 shape 为 (3, 4) 的 tensor 为例。LayerNorm 里面主要会用到三个参数：

normalized_shape：要实行标准化的最后 D 个维度，可以是一个 int 整数（必须等于tensor的最后一个维度的大小，不能是中间维度的大小），使用示例 tensor 的话此时这个整数必须为 normalized_shape=4，代表标准化 tensor 的最后一维。另外也可以是一个列表，但这个列表也必须是最后的 D 个维度的列表，如示例 tensor 的话就必须是 normalized_shape=[3, 4] 。

eps：为了防止标准差为零时分母为零，设置的极小值，默认是1e-5，也可以自己设置。

elementwise_affine：是否需要仿射变换。仿射变换需要两个可学习参数 γ 和 β：把标准化的结果乘以缩放系数 γ 再加上偏置系数 β。仿射变换是为了保证非线性的获得。

举个例子，我们有下面一个 shape 为 (3, 4) 的数组，并把它转化为 tensor。

import torch
import torch.nn as nn
import numpy as np
a = np.array([[1, 20, 3, 4],
               [5, 6, 7, 8,],
               [9, 10, 11, 12]], dtype=np.double)
b = torch.from_numpy(a).type(torch.FloatTensor)

3、举例-只对最后 1 个维度进行标准化

现在想计算对一个维度进行标准化，即对 [1, 20, 3, 4]、[5, 6, 7, 8,]、[9, 10, 11, 12] 分别标准化，可以像下面这样操作：

layer_norm = nn.LayerNorm(4, eps=1e-6) # 最后一个维度大小为4，因此normalized_shape是4
c = layer_norm(b)
print(c)
# 结果：
tensor([[-0.7913,  1.7144, -0.5275, -0.3956],
        [-1.3416, -0.4472,  0.4472,  1.3416],
        [-1.3416, -0.4472,  0.4472,  1.3416]],
       grad_fn=)

怎么验证对不对呢？我们可以使用 np 对数组 a 手动计算下标准化看看：

mean_a = np.mean(a, axis=1)  # 计算最后一个维度的均值 = [7. 6.5 10.5]
var_a = np.var(a, axis=1)    # 计算最后一个维度的方差 = [57.5 1.25 1.25]
# 对最后一个维度做标准化 减均值后除以标准差
a[0, :] = (a[0, :] - mean_a[0]) / np.sqrt(var_a[0])
a[1, :] = (a[1, :] - mean_a[1]) / np.sqrt(var_a[1])
a[2, :] = (a[2, :] - mean_a[2]) / np.sqrt(var_a[2])
print(a)
# 输出结果:
[[-0.79125657  1.71438923 -0.52750438 -0.39562828]
 [-1.34164079 -0.4472136   0.4472136   1.34164079]
 [-1.34164079 -0.4472136   0.4472136   1.34164079]]

这时发现与 torch 的 LayerNorm  计算结果想通过，印证了上述的解释。

4、举例-对最后 D 个维度进行标准化

这是个二维tensor，假设我们要对最后二维进行标准化，也即对所有数据标准化，可以令 normalized_shape=[3, 4]，如下：

layer_norm = nn.LayerNorm([3, 4], eps=1e-6)
c = layer_norm(b)
print(c)
# 计算结果：
tensor([[-1.4543e+00,  2.4932e+00, -1.0388e+00, -8.3105e-01],
        [-6.2329e-01, -4.1553e-01, -2.0776e-01,  1.1921e-07],
        [ 2.0776e-01,  4.1553e-01,  6.2329e-01,  8.3105e-01]],
       grad_fn=)

怎么做验证呢？也让 np 在所有数据上做标准化：

mean_a = np.mean(a)  # 计算所有数据的均值，返回标量
var_a = np.var(a)    # 计算所有数据的方差，返回标量
a = (a - mean_a) / np.sqrt(var_a)  # 对整体做标准化
print(a)
# 输出结果
[[-1.45434106  2.4931561  -1.03881504 -0.83105203]
 [-0.62328902 -0.41552602 -0.20776301  0.        ]
 [ 0.20776301  0.41552602  0.62328902  0.83105203]]

np 手动计算与 torch 的计算结果相同。